水下爆炸气泡射流载荷计算的新方法研究

余 俊，刘国振，汪 俊，王海坤

(中国船舶科学研究中心，无锡 214082)

1 引 言

水下爆炸可以划分为三个重要阶段，包括装药的爆轰、冲击波向外传播和气泡脉动等过程。水下爆炸过程中除了会向周围流体传递冲击波载荷外，爆轰产物形成的爆炸气泡在脉动过程中也会向外传递冲击载荷[1]。当爆炸气泡附近存在结构和自由面等边界条件时，在爆炸气泡溃灭过程中容易产生指向结构或者背向自由面的水射流现象。水射流产生过程中涉及到爆炸气泡、自由面或者结构边界和水等多物质和多界面之间的复杂耦合过程，研究难度非常大。目前对于气泡射流的理论分析仅限于简单规则的情形[2-4]，而实验研究的可重复性和可变性较差[5-7]，所以对气泡的数值模拟研究逐渐得到重视。目前对于水下爆炸气泡运动模拟的数值方法也比较多，其中边界元方法(BEM)普遍应用在气泡动力学模拟计算领域。BEM法计算维数降低，计算效率较高，在模拟三维复杂几何形状边界面时具有一定的优势。文献[8-10]在BEM方法的理论模型、计算方法和切割处理技术等多个方面开展了研究，使BEM方法得以不断补充和完善。BEM法在气泡脉动周期以及气泡最大半径等模拟方面具有较好的精度，但是在气泡溃灭阶段，由于水射流的高速运动以及水锤效应的存在，流场中的速度梯度较大，故需要考虑流体的可压缩性以及大变形等影响。此时BEM法的求解精度明显下降，难以适应高精度模拟的要求。除了边界元方法外，气-液两相流模型也是模拟气泡的重要方法，根据界面处理方法不同可以划分为界面追踪和界面捕捉两大类。界面追踪法是通过粒子点或标记等方法显式地追踪界面运动，比较适合简单的界面运动情况，难以描述界面复杂运动。而界面捕捉方法则是隐式地捕捉界面位置，主要以水平集法(level-set)[11]和体积分数法(vof)[12]为代表，在复杂界面运动模拟方面取得了大量广泛的应用。对于level-set方法，由于在数值通量守恒方面存在一定的不足，难以长时间精确捕捉界面运动过程。而vof方法是通过体积分数的对流方程来实现界面的捕捉，在长时间计算后界面容易出现弥散现象，界面出现模糊，从而影响计算精度。

由于上述计算方法在处理水下爆炸气泡射流阶段存在的困难和挑战，故难以精确获得水射流载荷的特征形式，无法对水射流载荷的冲击损伤效应进行准确评估。为了克服上述困难，本文拟在多相可压缩流体的 five -equation 计算模型基础上，引入界面函数和界面密度的压缩技术来提高水射流阶段气-液界面的捕捉精度，抑制界面弥散效应，从而建立爆炸气泡运动的数值计算模型。该模型采用5阶WENO重构与HLLC近似Riemann求解器进行空间离散，时间离散采用3阶TVD Runge -Kutta 法，能够捕捉冲击波的传播以及多相界面运动。针对该计算模型，首先通过三个典型的多相流问题算例进行考核，最后将该模型应用到水下近壁面爆炸过程中水射流现象的模拟，获得了水射流载荷的典型特征，为水射流的产生机理及其损伤效应的深入研究提供了技术支撑。

2 计算模型

2.1 控制方程

对于水下爆炸气泡运动等瞬态响应过程，可以忽略传热、粘性以及化学反应等影响，采用多相可压缩流体的 five -equation 模型对爆炸气泡及其周围流体之间的相互作用过程进行描述，其二维控制方程可表示为[13]

(1)

式中Q,F和G分别为

(2)

(z1)t+u(z1)x+v(z1)y=0

(3)

流体的状态方程采用刚性气体状态方程

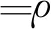
(4)

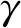
2.2 界面压缩与密度修正

基于体积分数的界面捕捉模型在计算过程中随着计算时间的推进，两相界面附近不可避免地会出现弥散效应，进而导致界面模糊不清。在流体产生涡旋和水锤现象的模拟过程中将显著影响流场的速度、压力和密度等关键物理量的计算精度，导致计算结果不可信。严重情况下会引起计算崩溃，从而使得计算模型的适用范围缩小，计算能力下降。特别是针对水下爆炸气泡脉动过程的模拟，气泡运动周期相对冲击波作用阶段长得多，采用显式计算格式的时间步长非常小，要想模拟气泡溃灭产生水射流的过程所需的计算步数特别长(一般在几万步以上)。如果不对界面弥散效应进行有效抑制，则计算结果将严重失真。

图1所示为未采用压缩技术计算的100 kg TNT在水深400 m工况下近壁面爆炸气泡收缩过程中崩溃形成的水射流现象，其中左侧为固壁条件，其他为透射边界，计算采用二维轴对称模型。图2为相同工况下采用压缩技术的计算结果，图3为上述两种计算工况下壁面中心点水射流压力的时程曲线。由上可知，如果不引入压缩技术，数值计算产生的气-液界面弥散效应将使得气泡射流撞击时头部水的密度急剧降低，导致射流的水锤效应不明显，水射流压力降低。由图3可以看出，水射流的峰值压力由77.8 MPa下降到49.2 MPa，下降幅度约为36.8%。

图2引入的界面压缩技术借鉴了文献[15-17]发展的界面压缩技术。首先将单相介质的质量守恒方程表示为

(5)

式中K=εh|z1|-z1(1-z1)，μ0为引入的系数，当μ0→∞时，要保证K=0，即在单相流体单元中式(5)右端趋于0，即此时界面不是0就是1，无需进行压缩。只有当z1∈(0,1)时，才对界面函数进行压缩。

图1 未带压缩下流场的密度和压力云图

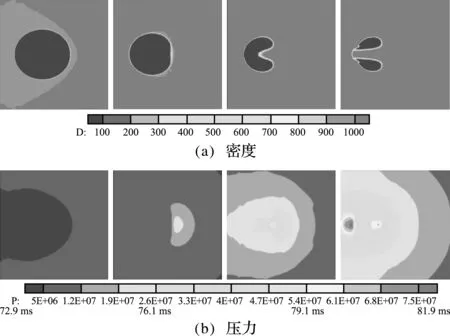
图2 带压缩下流场的密度和压力云图

在两相流中，除了界面位置会产生弥散外，密度在界面处也会随着时间弥散。本文直接给出质量守恒方程的界面压缩方程为

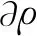
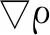
(6)

式中H(z1)=tanh{[100z1(1-z1)]2}。

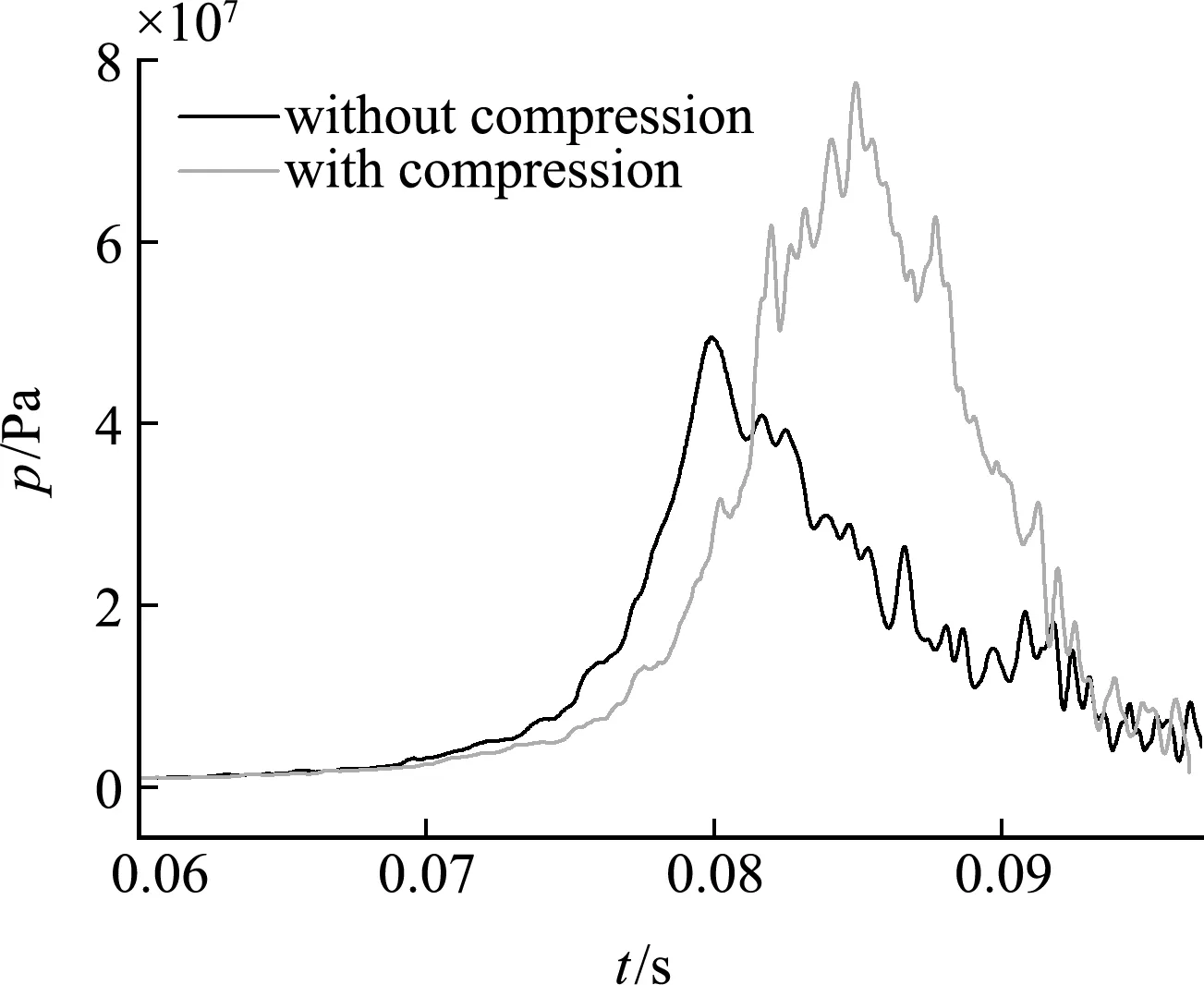
图3 壁面中心点处水射流压力曲线对比

3 数值离散

由于计算域中载荷强间断以及接触间断面的存在，采用有限体积格式进行空间离散[18,19]。将控制方程(1)在控制单元Ii j上进行平均积分，化简为

(7)

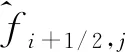
4 数值测试与验证

4.1 一维激波管问题

为了考核计算模型对冲击波传播以及界面运动的捕捉能力，采用一维Sod问题来进行测试，模拟的是较为复杂的Sod激波管问题，一般是用来分析水下爆炸的气-液两相运动问题[22,23]，无量纲参数的初始条件为

(8)

4.2 二维激波管问题

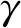
图4 计算结果与精确解对比

(9)

图5给出了激波作用R22气泡后典型过程的计算结果(密度云图)与试验结果对比，R22气泡从开始压扁，到继续变形以及形成上下两个典型漩涡的过程。计算结果与试验结果吻合较好，证明了本文的计算模型能够较为精确地捕捉激波的传播以及多相流体界面的运动过程。

图5 二维气泡运动过程的密度云图计算与试验对比

5 水下近壁面爆炸气泡射流现象

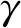
装药爆轰采用瞬时爆轰模型，流场初始条件为

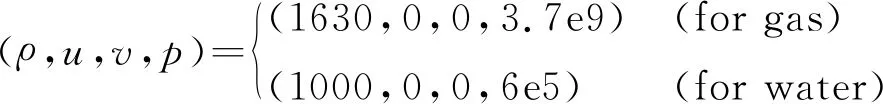
(10)

可以看出，气泡在21.2 ms时刻附近膨胀到最大体积，接下来气泡开始收缩过程，周围流体对气泡进行压缩。由37.1 ms时刻流场的压力云图可知，在气泡收缩过程中，左侧气泡壁与固壁之间流场压力较低，两者之间的相对运动处于较为平衡状态，而右侧气泡壁附近流场中存在局部高压区，使得气泡壁面加速向左运动。由于气泡表面运动的非均衡性，在气泡收缩过程中右侧气泡壁逐渐出现凹陷，开始产生射流形态，并冲击左侧气泡壁。在39.3 ms附近射流开始冲击左侧气泡壁，出现水锤现象，在壁面附近产生局部高压，开始向外辐射压力。之后爆炸气泡也由开始的单连通域演变成多连通域，出现涡环现象，接下来开始气泡的第二次脉动过程。

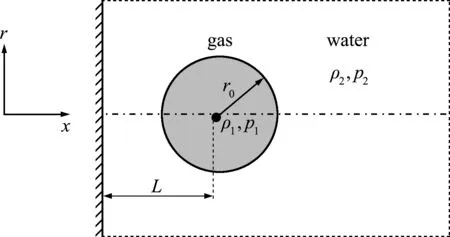
图6 近壁面水下爆炸计算模型

图7 近壁面水下爆炸的密度与压力演化过程

图8所示为在水射流出现阶段爆炸气泡的等效半径与壁面中心点处流场的压力时程曲线，图中标出了与图7对应的部分典型时刻在压力曲线上的位置。从图9可以看出，39.3 ms时刻射流开始冲击左侧气泡壁时，水射流压力仍处于上升阶段，气泡仍处于压缩阶段。39.8 ms水射流压力达到峰值压力46.8 MPa，此时锥型水柱主体部分作用到左侧气泡壁。之后随着水射流能量的逐步消耗，压力也逐渐下降。在压力下降过程中出现的部分震荡现象，结合图7可以看出，此时气泡界面并不完整，出现多连通域。在射流撞击产生冲击波及其传播的过程中，容易叠加部分高频震荡。图9为39.3 ms时刻流场中水平方向的速度分布云图，最大速度超过了280 m/s。

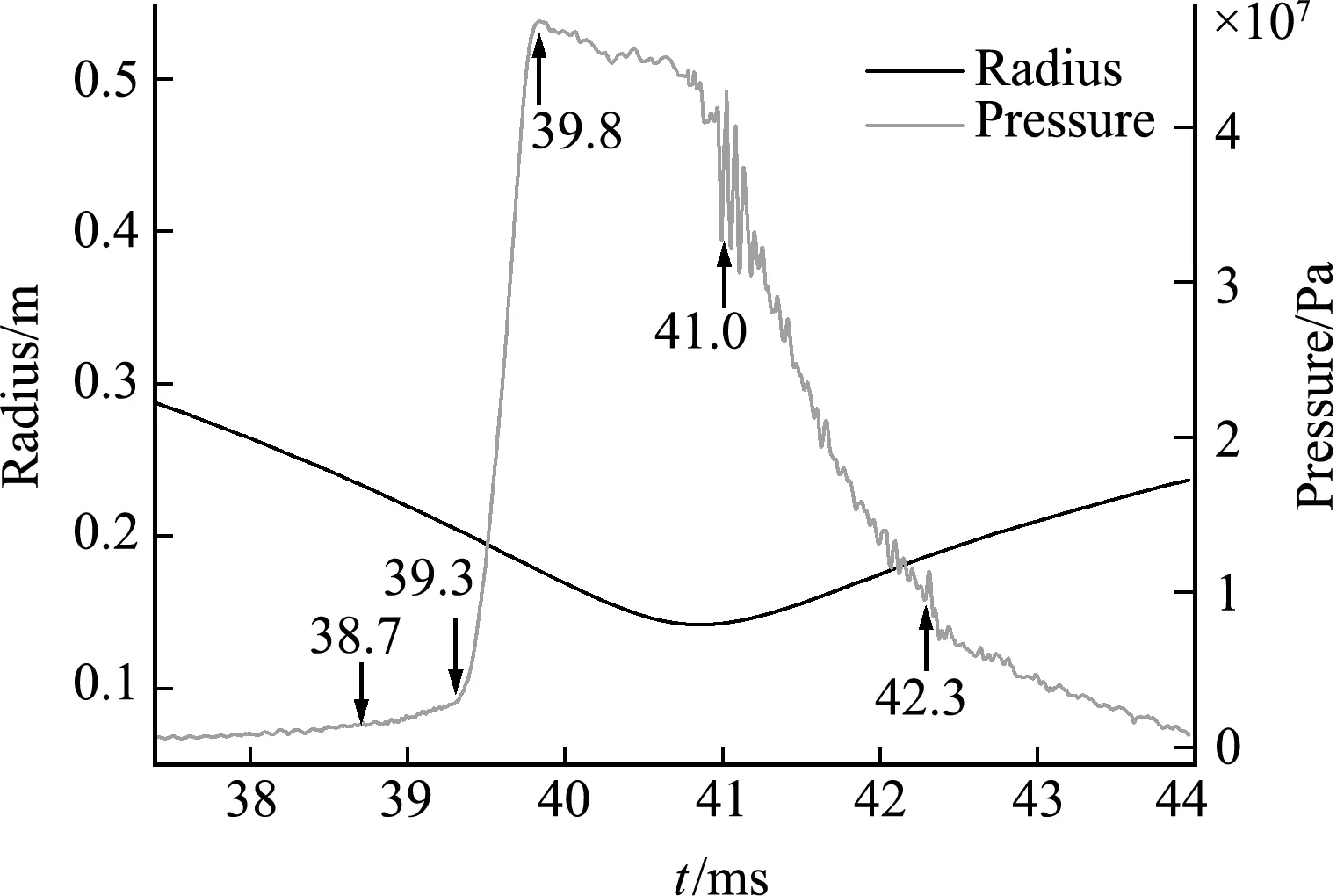
图8 爆炸气泡等效半径与壁面中心点压力的曲线

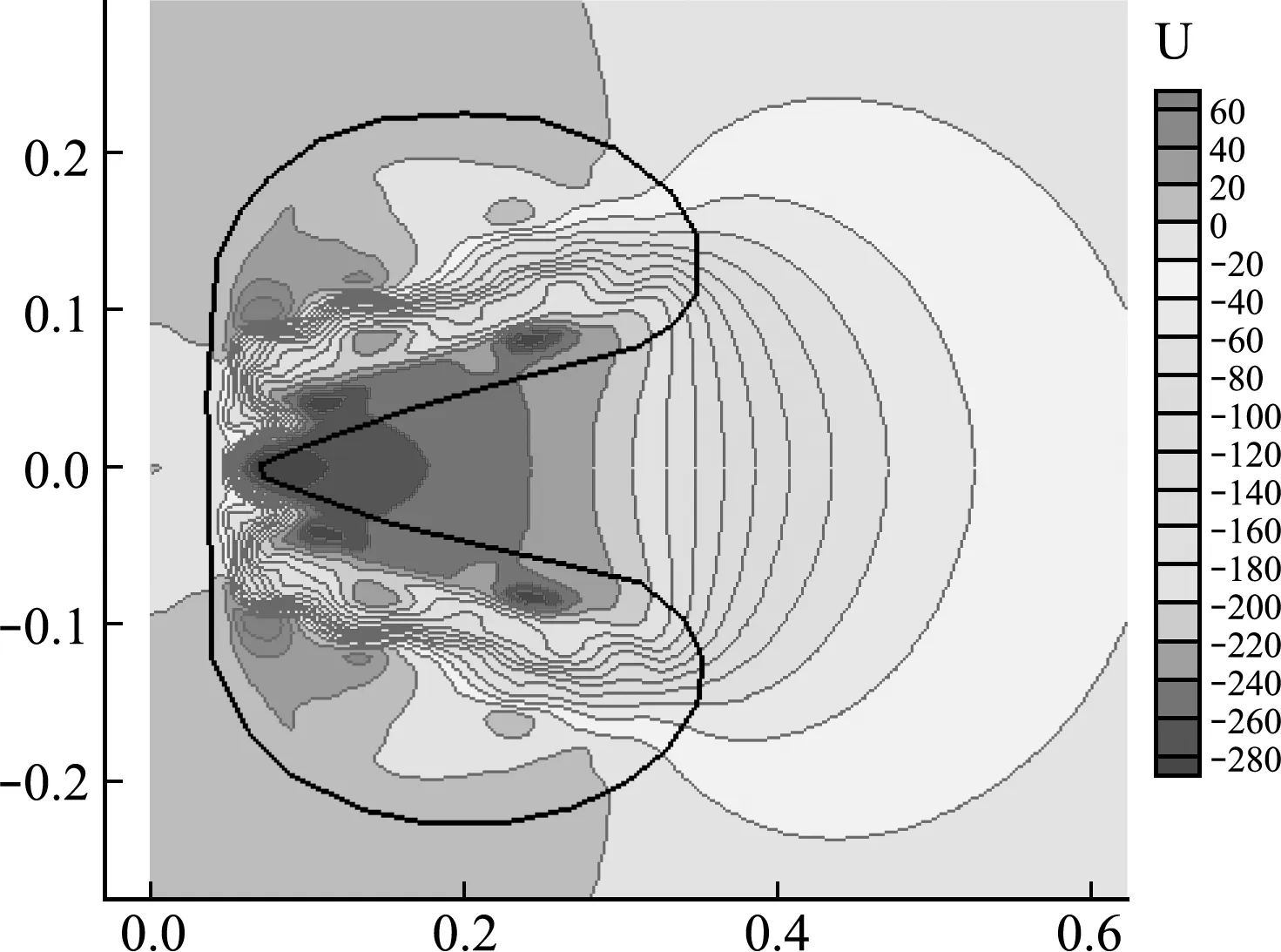
图9 流场中水平方向速度分布云图

6 结 论

本文基于多相可压缩流体的 five -equation 计算模型，引入界面函数压缩和密度修正等技术来克服水射流演化过程中出现的界面弥散效应，获得了近壁面水下爆炸爆炸气泡运动的典型过程，获得了水射流冲击壁面产生的直接载荷特性。研究结果表明，水射流载荷的峰值压力较大，且有效作用时间较长，其对于附近结构的冲击损伤不能忽略。虽然目前针对水下爆炸气泡溃灭及其壁面效应的实验结果较为丰富，但由于水射流方向的随机性以及测试技术的限制，目前对于水射流直接载荷的测量数据少见。后续拟在此方面开展相关研究，进一步考核验证本文的计算模型，使之更加精确适用。