涡激响应尾流双振子模型的参数反演方法

颜凝雨，杨自豪*，张洁琼，林 巍，刘孟源

(1.西北工业大学 数学与统计学院，西安 710072；2.中交悬浮隧道工程技术联合研究组，珠海 519000)

1 引 言

任何非流线型物体在一定的恒定流速下，都会在物体两侧交替地产生脱离物理结构表面的周期性漩涡，从而诱发弹性支撑结构物的涡激振动现象VIV[1]。大量实际工程问题中，许多圆柱结构，如悬浮隧道、深水立管、高空桅杆和新型风力发电等，均可能出现涡激振动现象。虽然合理利用涡激振动会为人们带来便利，但其诱发的共振也会对结构产生较大的疲劳损害。

研究圆柱结构的涡激振动主要有试验法[2-4]、数值方法[5,6]和经验模型[7,8]。试验方法虽然直观可靠，但成本较高；数值方法虽然在计算精度上占有一定优势，但计算较为复杂，尤其是在高雷诺数的情况下。而经验模型可较快计算涡激振动的主要特征，还可以在模型的指导下设计试验或者研究某个参数对试验结果的影响，因此经验模型法正受到国内外诸多学者的关注，其中尾流振子模型是应用较为广泛的一种模型。

Bishop等[9]认为流体的尾流对圆柱体结构的作用相当于一个非线性振子，首次提出了尾流振子模型。之后，Hartlen等[10]将Vander Pol方程与结构振动方程联立，使尾流振子模型更加具体化。Skop等[11]进一步改进了Hartlen的模型，对模型经验参数进行了研究；Landle[12]提出了一个拥有五阶非线性气动阻尼项的无量纲尾流振子模型；Facchinetti等[13]通过分析对比发现加速度耦合模型可以更准确地定量预测涡激振动的基本特征；Ogink等[14]对Facchinetti的尾流振子模型建立过程进行了具体分析，通过引入频率耦合变量进一步改进了模型。但上述对尾流振子的研究大多针对横向单自由度，而实际的涡激振动中横向振动和顺流向振动往往相互影响，许多学者也针对双自由度的尾流振子模型做了研究。Krenk等[15]根据流固耦合的能量流平衡原则构建了双振子模型；Srinil等[16]提出了一种改进的用于预测均匀流中柔性圆柱体的二维耦合尾流双振子模型。康庄等[17]建立了非线性结构振子和流体振子的耦合模型，可以较准确预报低质量比圆柱结构双自由度涡激振动的特征。Yang等[18]提出一种新的涡激振动非线性耦合尾流振子模型，其只使用一个尾流振荡器来耦合横向和顺流向的运动。在实际应用中，不是所有模型的参数都可以通过物理方法测量得到，尾流振子模型的应用往往面临参数选取的难题，参数选取的偏差可能导致计算结果的不准确，从而无法充分发挥经验模型在研究涡激振动问题中的优势。

解决复杂模型参数反演问题的方法有很多种，其中神经网络方法以其高速寻优和自学习等优势在参数反演问题中得到广泛的应用，如Spichak等[19]运用BP神经网络求解地电三维逆问题，证实神经网络方法可以成功地用于地电三维逆问题参数反演；Cerdena等[20]在测定海洋层积云物理性质的研究中，运用遗传算法优化的BP神经网络对辐射传输模型中的参数进行了反演；Zhao等[21]提出一种人工蜂群算法优化的BP神经网络，并对岩土工程中的模型参数进行了反演。国内外没有针对尾流振子模型参数反演的研究工作。

本文研究尾流双振子模型中参数的反演方法。首先利用降阶法将模型变为一个常系数多变量的非线性一阶常微分方程组，并利用龙格-库塔方法进行求解。设计悬浮隧道物理模型的水槽试验，在给定的多组物理参数和试验数据下，构建最优化模型，利用遗传算法优化的BP神经网络智能算法反演未知参数。

2 涡激响应尾流双振子模型

柔性圆柱结构双自由度涡激振动模型[16]如 图1 所示。假定直径为D的圆柱结构无限长，水平和竖直方向，即X和Y两个方向的弹簧刚度分别为Kx和Ky,水的流速为V,圆柱体受到双向四个弹簧的作用力，在X和Y两个空间方向上自由振动，无量纲形式的涡激响应尾流双振子模型可表示为[16]

(1)

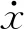
图1 柔性圆柱结构双自由度涡激振动

λx=2ξxf*+γΩ/μx,λy=2ξy+γΩ/μy

(2)

式中ξx和ξy为结构水平和竖向运动阻尼比，取值范围为[0.01,0.08]；f*为X和Y两方向结构固有频率之比，取值范围为[0.5,1.5]，γ为Stall参数，取值为0.8；Ω=St·Vr为静水中旋涡脱落频率与圆柱横流固有频率之比，St为Strouhal数，取值为0.2，Vr=V/(Dfn)为约化速度,fn为Y方向结构固有频率，μx和μy表达式为

(3)

此外，(αx,αy,βx，βy)为无量纲几何非线性系数，表征位移非线性项对本身的影响。MD和ML为系统质量参数，

(4)

式中CD 0和CL0分别为静置圆柱结构的阻力和升力系数，取值为0.2[16]和0.3；St为斯特鲁哈尔数，取值为0.2；εx和εy为尾流系数；Λx和Λy为经验耦合参数，均取为12。

对于质量分布均匀的圆柱体，有

(5)

且可取εx=0.3，εy由试验数据拟合得到，其拟合表达式为

εy(m*)=b1eb2 m*

(6)

式中b1=0.00234，b2=0.228。

由式(1)可知尾流双振子模型是一个多变量的二阶非线性常微分方程组，现运用降阶法将该模型化为一个常系数多变量的一阶非线性常微分方程组。引入如下变量

u=(u1,u2,u3,u4,u5,u6,u7,u8)T=

(7)

式中T为矩阵的转置。方程组(1)可转化为一阶常微分方程组(8)。

(8)

进一步，式(7，8)可以改写为

(9)

式中M和g的定义如下

(10)

g(t,u,αx,αy,βx,βy)=(g1,g2,g3,g4,g5,g6,g7,g8)T

式中

g1=u5，g2=u6，g3=u7，g4=u8

MDΩ2u2-2πMLΩ2(u4u7/Vr)

MLΩ2u4+2πMDΩ2(u2u7/Vr)

(11)

给定初值u0,该一阶非线性常微分方程系统可使用经典的龙格-库塔方法进行求解。

3 圆柱结构涡激振动响应水槽试验

3.1 试验目的

尾流双振子模型中(αx,αy,βx，βy)四个参数表征位移非线性项的影响，无法通过试验直接测得，其他参数均可通过试验或经验获得。若想得到上述四个参数的值，由模型(9)可知，一种可行的方案是通过圆柱体涡激振动时的位移数据来反演这四个未知参数。因此，本节设计圆柱结构的水槽试验，测得圆柱结构在不同水流力(流速)作用下水平和竖直方向的位移时间序列及运动轨迹。

3.2 试验设计

现有的圆柱结构涡激振动试验不考虑悬浮隧道等实际工程结构试验节段的真实刚度，试验结果无法反映真实结构的刚度和自振频率，试验结果与实际值误差较大。本节给出新型的圆柱结构水槽试验设计方案。

首先运用等效固有振频法计算悬浮隧道等实际工程结构某一节断的真实刚度值k0,计算公式为

k0=(4π2m)/T2

(12)

式中m为某一节段的质量，T为该节段在水中的固有频率。其次根据相似准则，将真实刚度k0按照比尺换算成试验模型的刚度k1,并据此配置水平和竖向弹簧的刚度。最后将试验模型放入水池中进行试验，浮筒式试验装置如图2所示。

图2 试验装置设计

试验采用直径为8 cm和长度为70 cm的透明树脂材料制成的空心圆柱体模拟深海悬浮隧道等实际工程结构的节段(等刚度模型)，模型重 3.3 kg，浮重比1.07，试验比尺为 1∶157.5。圆柱体使用4根弹簧与透明固定板链接，其中横向和竖向弹簧刚度分别取为30.6 N/m和21.6 N/m，弹簧原始长度均为100 mm，圆柱体、弹簧和透明固定板之间均采用L型钢扣栓接，如图3(a)所示。静止状态下，弹簧长度为192 mm，如图3(b)所示。

选取天津水运工程科学研究院水槽厅的波流水槽为试验场地，水槽宽70 cm，长30 m，水深 57 cm，造流范围为0.02 m/s～0.5 m/s，水槽尾端采用斜坡式消波框防止波浪反射。将试验模型放入0.5倍水深处进行试验，并在模型截面贴上红色方块标志点，如图3(b)所示。不断改变水的流速，利用相机对标志点进行动态捕捉，然后利用 Matlab 编写的视频识别程序，抓取每一帧中标志点中心的位置，并将前后两帧位置数据进行比较，从而得到圆柱体在不同物理流速下水平和垂向位移随时间变化的数据。试验共进行9组，每组试验所对应的水的流速和约化速度列入表1。

图3 试验装置

表1 9组试验中水的流速和约化速度Tab.1 Water velocity and reduced velocity in 9 sets of tests

3.3 试验结果

不同流速下圆柱结构的运动轨迹经过无量纲处理后如图4所示。可以看出，运动轨迹呈8字形，且随着流速的增大，模型在竖直方向的运动幅度增大，在第五组达到最大，考虑可能达到了锁定流速区间，即当流速在此区间内时，圆柱结构振动频率近乎不变，振幅维持较高水平；且随着流速增加，模型所受横向拖拽力增加，无量纲横向位移一直增大，这与以往研究保持一致[8]。

4 参数反演的BP神经网络模型

4.1 参数反演的最优化模型

根据第3节中每组试验，可以得到对应的位移试验数据

(i=1,…,n;ti∈[0,tmax](13)

而每给定一组参数(αx,αy,βx，βy),求解微分方程系统(9)，可得到对应的位移计算数据，记作

x(t,αx,αy,βx,βy),y(t,αx,αy,βx,βy)

(t∈[0,tmax])

(14)

下面构建参数反演的最优化模型，即求(αx,αy,βx,βy),使

(15)

由于本文关注的核心为振子的幅值和均方根，因此可引入向量函数

opt(x,y)=[rms(x),rms(y),max(x),max(y),

min(x),min(y)]T

式中max(·)和min(·)分别为向量的最大和最小分量，rms(·)为均方根。

N为向量x的长度。目标函数可以取为

(16)

求解最优化问题(15，16)即可得到未知参数的一组最优值。

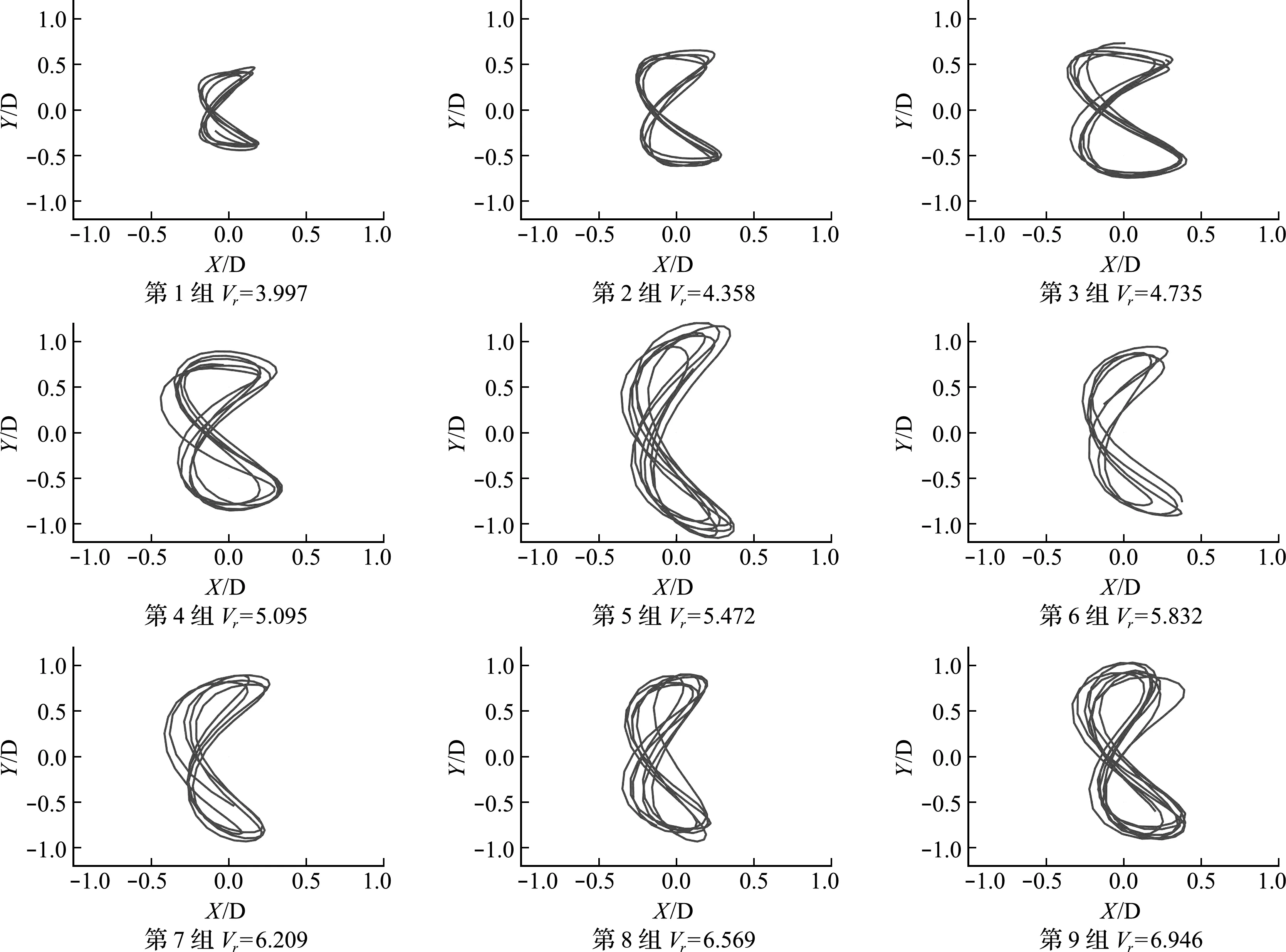
图4 不同流速下圆柱的运动轨迹

4.2 BP神经网络的构建

人工神经网络是一种由大量处理单元互联组成的非线性、自适应信息处理系统，具有快速求解最优化解的能力，其最小最重要的单元叫神经元，每个神经元都有输入连接和输出连接，这些连接模拟了大脑中突触的行为，每一个连接都有对应权重。BP神经网络由输入层、隐藏层和输出层构成，是一种按误差反向传播训练的多层前馈网络。BP神经网络求解优化问题的基本思想是利用BP算法，通过信息的正向传播和误差的反向传播，不断调整网络中的权值和阈值，使输出和样本的实际标签之间的误差达到最小。涡激响应尾流双振子模型的参数反演思路为，生成多组未知参数数据，通过求解尾流双振子模型(9)得到每组未知参数下的位移时间序列数据；分别计算每组竖直和水平位移数据的最大值、最小值和均方根，并以这6个数据作为神经网络的输入，以未知的4个参数为输出，优化目标为式(15)，即可训练出对应的神经网络模型；将试验得到的一组位移数据代入已训练好的神经网络，即可输出一组未知参数的值。

4.3 基于遗传算法优化的BP神经网络

BP神经网络存在局部极值，误差较大。现采用遗传算法对BP神经网络进行优化，即使用遗传算法对BP神经网络的初始权值和阈值进行优化，进一步提高参数反演的精度。遗传算法以优胜劣汰的自然选择和基因阶段的遗传变异原理作为基础，是一种具有很强随机搜索能力的智能算法，可以取得很好的搜索效果。遗传算法对BP神经网络的优化，实际上是对BP神经网络的初始权值和阈值进行优化。首先确立BP神经网络结构并得到一组初始权值和阈值，遗传算法将对其编码，并再次通过神经网络训练，得到的误差作为适应度。然后不断经过选择、交叉和变异操作使适应度逐渐增加，最终满足精度条件，得到最优权值和阈值。最后再代回BP神经网络进行求解。具体流程如图5所示。

4.4 参数设置及误差定义

尾流双振子模型的参数取值列入表2。

反演数据与试验数据的误差计算公式为

(17)

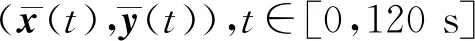
表2 参数取值

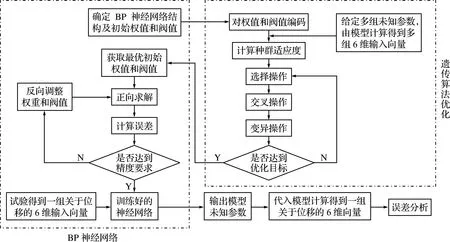
图5 求解参数反演问题分析流程

5 参数反演结果分析

利用遗传算法、BP神经网络算法和基于遗传算法优化的BP神经网络算法反演参数。遗传算法中初始种群数目取为20，进化代数取为80，交叉概率取为0.95，变异概率取为0.001。BP神经网络由一个输入层、一个隐藏层和一个输出层构成，网络模型参数选取如下，输入层神经元个数取为6，隐藏层神经元个数取为8，输出层神经元个数取为2，数据库样本个数取为8000，训练集个数取为7200，验证集个数取为800，训练误差目标取为10-4，学习效率取为0.4，传递函数取为{tansig,purelin}，未知参数αx和αy的取值范围为(0,1)，未知参数βx和βy的取值范围为(0,10)。此外，每组试验数据分别训练50次，取平均值作为参数的最终预测结果。需要指出的是，由于试验误差，试验得到的位移数据没有呈现稳定后的周期震荡模型，但大致稳定在某个固定区间之内。为了减小参数反演误差，现对神经网络的输入参数，即竖直和横向位移的最大和最小实验数据做以下处理，以第3组试验的水平方向位移最大值为例，利用Matlab程序找到数据的峰值，再求出峰值的平均值作为神经网络位移最大值的输入，如图6所示。基于遗传算法优化的BP神经网络算法流程如图5所示，其中遗传算法和BP神经网络的初始参数如前所述。

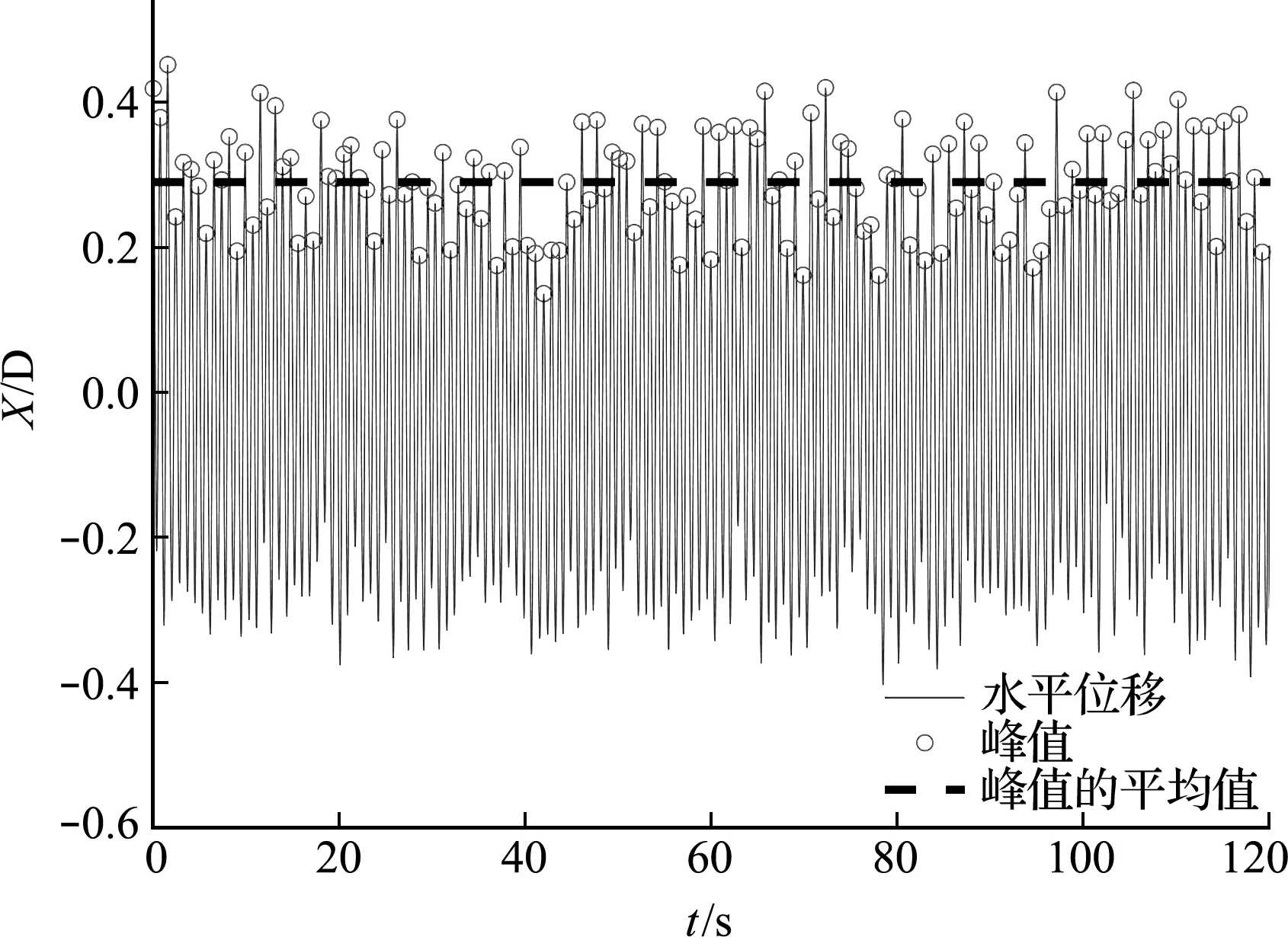
图6 试验数据输入最大值的处理

利用遗传算法、BP神经网络算法和基于遗传算法优化的BP神经网络算法反演参数的误差Ret列入表3，误差随水的流速变化如图7所示。由表3可知，三种方法所得结果的平均误差分别为10.37%、7.53%和5.50%，基于遗传算法优化的BP神经网络算法的平均误差相比遗传算法和BP神经网络算法分别降低了46.96%和26.96%。此外，由图7可知，遗传算法的稳定性最差，BP神经网络次之，遗传算法优化的BP神经网络的稳定性最好。遗传算法优化的BP神经网络参数参演结果列入表4。

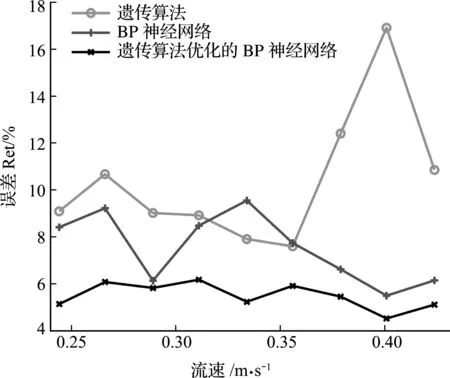
图7 三种模型方法的误差比较

图8为利用遗传算法优化的BP神经网络的反演结果与第3、4和第6组试验无量纲位移数据的对比，其中图8左图分别表示第3、4和第6组试验方法与反演方法水平和竖直方向无量纲位移数据的对比，图8右图分别表示第3、4和第6组试验数据与反演数据水平和竖直方向运动轨迹的对比。可以看出，基于遗传算法优化的BP神经网络算法反演结果与试验结果吻合较好。因此，基于遗传算法优化的BP神经网络智能算法能够精确稳定实现尾流双振子模型的参数确定。

表4 遗传算法优化的BP神经网络参数反演结果Tab.4 Parameter inversion results of BP neural network optimized by genetic algorithm

最后以第3组参数反演问题为例进行灵敏度分析，研究反演参数的微小偏差对反演精度的影响。将两个参数值分别在参数反演结果附近微小扰动，图9给出了误差Ret的值，其中灰色点代表遗传算法优化的BP神经网络参数反演结果。

可以看出，参数反演结果处于在局部最优解附近，进一步验证了反演方法的正确性。此外，通过计算误差沿两个参数的变化率可发现，误差Ret对参数βx和βy更加敏感。在反演结果(0.8214±0.2，10.0674±0.5)附近的参数取值(灰色实线区域)对应的误差Ret约为6%，在反演结果(0.8214±0.5，10.0674±1)附近的参数取值(灰色虚线区域)对应的误差Ret约为10%。该灵敏度分析结果可为类似问题的参数取值提供可靠的理论分析基础。

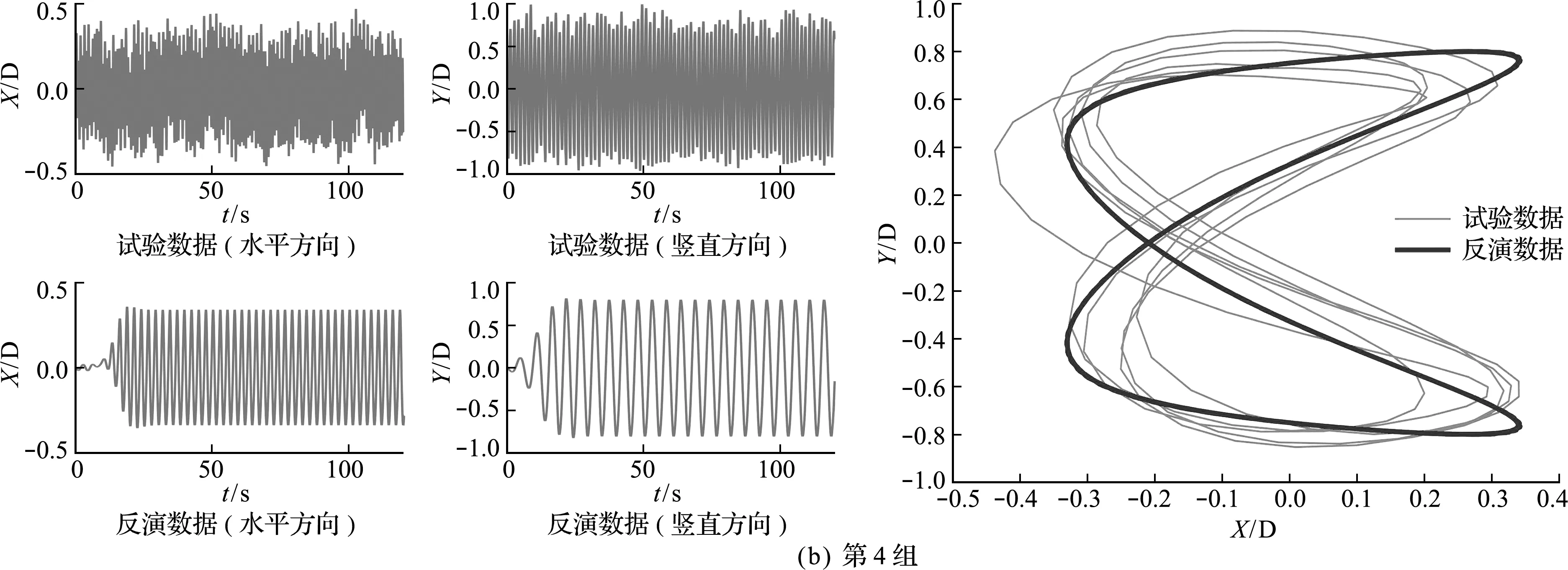
图8 第3、4和第6组试验位移数据与反演数据对比

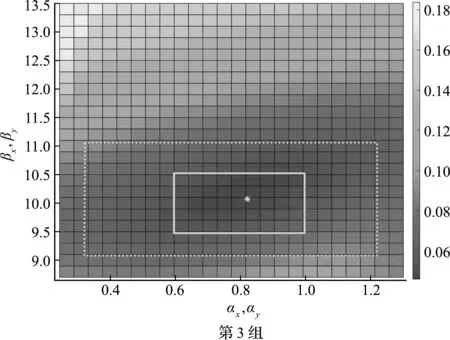
图9 第3组参数反演问题中的参数取值域

6 结 论

本文主要研究了尾流双振子模型中未知参数的反演方法，给出了基于物理试验和BP神经网络模型的参数反演方法。利用降阶法将尾流双振子模型转换为一阶常微分方程组，并使用龙格-库塔方法实现模型的求解。给出了一种新型的圆柱结构水槽试验设计方案，获取了圆柱结构在水平和竖直方向的位移试验数据。基于试验数据，构建了最优化模型，并利用基于遗传算法优化的BP神经网络算法对尾流双振子模型中四个未知参数进行了反演，误差处于可接受范围之内。本文的工作将为悬浮隧道等实际工程结构的涡激振动响应分析提供理论基础。