气体速度对液膜在预膜板表面流动形态影响的LBM模拟

于蔚然，周 训，李维仲

(大连理工大学 海洋能源利用与节能教育部重点实验室，大连 116024)

1 引 言

在自然界及工程界普遍存在的气液两相流动现象中，两相流因其复杂的流体系统和气液相界面的不断变换，是一项具有挑战性的研究工作，因此该问题备受科学研究者的关注。气流通过界面剪切力驱动的液膜流动是一种典型的两相流动形式，也是许多传热传质设备中常见的流动形态。在航空发动机的喷雾装置中，带有预膜板的气动雾化喷嘴在进行雾化的过程中，高速流动的气体会通过界面剪切力驱动液膜在预膜板上流动并产生波浪形的气液相界面变化，且气液层有较大的密度比，同时气体雷诺数也明显高于液体。研究表明，气流的剪切作用对液膜铺展及流动形态有着重大影响。由于气液在预膜板上的流动形态直接影响预膜板唇边后部的液体雾化质量，因此，探寻不同气体速度对液膜流动形态的影响规律，对于后期液膜破碎机理的研究有着重要意义。针对气体速度对液膜流动的影响，已有研究结果显示[1,2],气流的加速会导致液膜的传播速度增强，进而影响液膜界面的变化。本文将针对该问题进行深入的探寻并总结相应的规律。

关于液膜流动问题，已有诸多理论分析[3,4]、实验[5,6]及数值模拟对其进行相关研究。但对于相界面的追踪，数值模拟方法的优越性尤为明显。目前对于多相流的数值模拟方法较为常用的是VOF和Level Set方法，此类方法已成熟地运用在液膜流动、液滴运动和沟流等模拟[7,8]上。这类流动属于自由表面的流动，周围气体对流动的影响微乎其微，往往在数值模拟中较好处理。但是由于较高气流剪切作用下气液相界面会出现复杂的拓扑形变，VOF和Level Set难于准确追踪界面位置，且现有方法很难处理气液界面处两相大密度比问题，因而找到一种可以合理处理相关问题的方法显得尤为重要。格子玻尔兹曼LBM(Lattice Boltzmann method)[9]，一种基于分子动理论的模拟流体流动的数值方法,在经过近些年的不断发展和完善后，目前已广泛应用于多相流、湍流、相变传热和微通道驱替[10-12]等多种复杂物理现象的模拟。发现LBM在追踪具有较大拓扑形变的相界面演化过程中有着独特的优势。针对用于多相流的LBM模型，现有模型大多只能处理中小密度比的两相流体流动[13-16]。在涉及大密度比的多相LBM模型中，Liang等[17]提出的基于相场理论的LBM模型在降低假速度和保持质量守恒方面有着出色表现。从理论上讲，该模型的界面捕捉方程采用的是AC(Allen-Cahn)方程，由于该方程具有比CH(Cahn-Hilliard)方程低阶的扩散项，因此其在计算序参数及密度场等方面具有比基于CH方程模型[18]更高的数值精度和稳定性，同时在界面捕获中也有相应的优势，因而选择该模型处理本文提出的问题不失为良好的选择。但在使用Liang等[17]模型进行计算时，由于基于相场理论的LBM模型在两相界面附近存在密度变化，该处的连续性方程不满足不可压缩性条件。因而本文在上述模型中引入额外的界面力来消除此影响。

概括来看，本文首先对Liang等[17]提出的LBM模型进行修正，从而提升模型计算准确性。进而将该模型用以模拟计算本文所研究的高密度比气液两相流问题，探寻气体速度对液膜流动形态的影响，最后总结规律。

2 数学方法

2.1 基于相域理论的LBM两相流模型

2.1.1 控制方程

本文所采用模型包含两组LB方程，一组用于求解界面捕捉的AC方程，一组用于求解不可压缩的Naiver-Stokes(NS)方程。其中，AC方程[19]为

(1)

式中n为界面处的单位法向量，

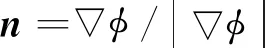
(2)

而对于式(2)的λ，其定义式为

(3)

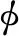
对于不可压缩流体，带外力项[20]的NS方程可表示为

·u=0

(4a)

(4b)

式中F为外力项总和，详见下文。

2.1.2 AC方程的LBM演化方程

基于BGK假设，AC方程的LBM演化方程可写为

(5)

(6)

式中ωi为权系数，其数值取决于所选择的格子玻尔兹曼模型。对于本文所选D2Q9模型，ωi的取值为ω0=4/9,ω1 - 4=1/9,ω5 - 8=1/36，离散速度ci为

(7)

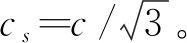
在式(5)中，外力源项Fi的定义式为

(8)

(9)

(10)

(11)

2.1.3 NS方程的LBM演化方程

含外力项的NS方程的格子Boltzmann-BGK演化方程可以表示为[22]

δtGi(x,t)

(12)

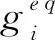
(13)

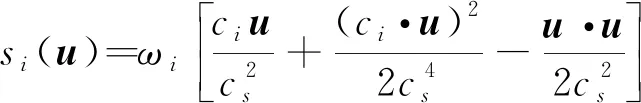
(14)

式(12)的外力源项Gi与现有LB模型中[23-25]的表达式不同，本文采用更为简单的形式：

(15)

式中F为总的外力项。

F=Fs+Fa+G

(16)

式(16)为计算中可能出现的体积力，Fs为表面张力。

(17)

式中β和k的取值与界面厚度以及表面张力系数σ有关。

(18)

基于相场理论的LBM模型在两相界面附近存在密度变化，该处的连续性方程不满足不可压缩性条件，为了消除此影响，本文引入一个额外的界面力Fa=qau来提高模型的准确性，其中参数qa的计算式为

(19)

在此基础上，宏观速度和压力的计算公式修正如下：

(20)

(21)

另外，通过Chapman-Enskog展开，流体运动粘度由式(22)确定。

(22)

要注意的是，在两相流体系中，运动粘度系数是在变化的，为了使其在界面处平滑过渡，通常的处理办法是将运动粘度系数当作序参数的线性或逆线性函数[15,26]。考虑到更简单的情况，本文采取了线性形式计算该参数，

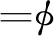
(23)

式中υl和υg分别为液气两相的运动粘度系数。

3 模型验证

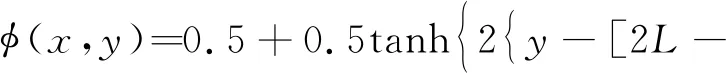
(24)

模拟过程中，计算域上下壁面为无滑移边界，左右壁面为周期边界，网格量设定为256×1024。

图2为Re =2048，At=0.5时，由R-T不稳定性引发的两相界面随时间的演化过程。可以看出，由于初始时刻两相界面存在扰动，在重力作用下，密度大的流体往下沉(spike)，密度小的流体向上浮(bubble)。当两种流体间的剪切速度差足够大时，则会触发Kelvin-Helmholtz不稳定性现象，从而使相界面处出现卷曲变形。图2相界面的演化过程与文献[27,28]的计算结果基本一致。

通过以上结果证实了该模型在低密度比下捕获R-T不稳定性特征的能力，但对于修正后的模型在计算高雷诺数下具有大密度比的问题，其可靠性没有得到充分的验证，因此接下来本文将进一步对该模型进行验证计算。文献[17,29]指出，在R-T不稳定性发生初期，界面扰动呈指数型增长，增长规律为

a=a0eα t

(25)

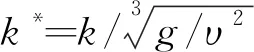
图1 R-T不稳定性示意图

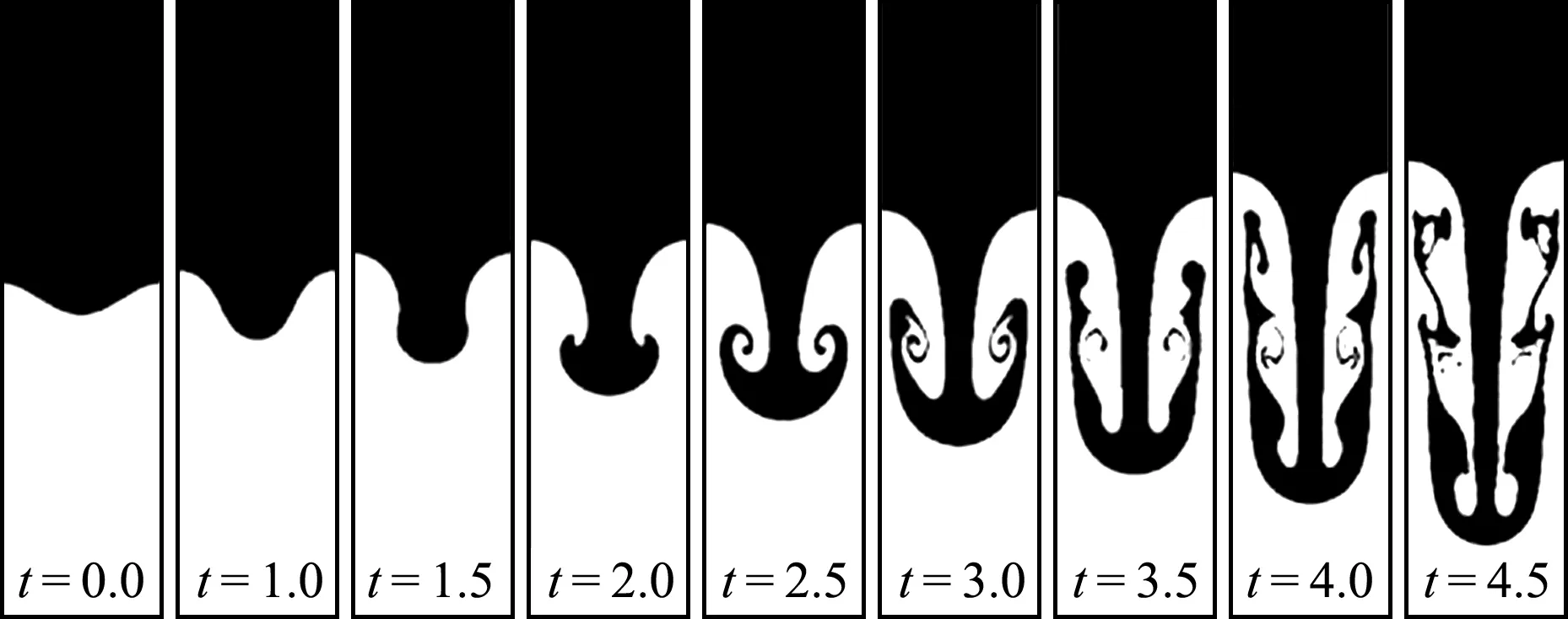
图2 Re=2048,At=0.5时R-T不稳定性现象中界面形态随时间的演化

4 模拟结果与讨论

为了探究在高速气流驱动下液膜在水平预膜板表面的流动状态，构建如图4所示的两相流体系，气体层和液体层厚度分别为Hg和Hl，气液初始速度分别为Ug和Ul，且Ug>Ul。液体进口速度给定为

ux(y)=Ultanh(y/δ)

(26)

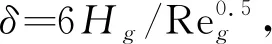
(27)

图3 不同k*下增长率α*的计算结果与文献[17]和

解析解[29]的结果对比

Fig.3 Comparison of the dimensionless growth rate obtained from the present model with ref.[17] and analytical data[29]

图4 液膜流动计算域

式中y为计算域竖直方向各点纵坐标值。气相初速度给定为

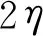
(28)

图5给出了在Reg=5592.377(表1中 Case 3)时液膜在预膜板表面铺展形态的变化。随着演化的进行，可以看出在气流的剪切作用下，液膜表面逐渐形成波浪形突起并向右推进，直至离开计算区域。液膜表面形成波浪形突起是由于气液两相间的速度差造成的Kelvin-Helmholtz不稳定性引起的，这与Baptiste等[30]对该速度比下的液膜流动形态描述相符。

图6分别描绘了表1中Case 1～3不同气流速度下气液相界面的变化。可见随着气体速度的增大，气体驱动液膜形态改变的进程也在加快，流体界面波动幅度增大。事实上，随着入口气体速度的增加，气液间的剪切速度差也随之增加，较高的速度差会导致更强的Kelvin-Helmholtz不稳定性现象，从而在气液界面掀起更高振幅的波浪。为了更好地比较气流速度对气液相界面波动的影响，本文统计了计算域中液膜的厚度峰值A随时间的变化。如图7所示，纵坐标A/Hl代表各时刻液膜厚度峰值与初始液膜厚度的比。随着演化的开始，气液间的剪切速度差引起的Kelvin-Helmholtz不稳定性现象使相界面出现扰动，液膜表面出现表面波，液膜厚度峰值有所提升，并随着演化的进行不断波动。当气体速度较小时，液膜在气体剪切力作用下产生较小振幅的表面波并向前推进直至流出计算域，待气液两相体系稳定后气液界面会出现周期性微小波动，液膜厚度基本保持稳定。随着气体速度的提升，液膜表面出现更为频繁且大振幅的波动。当Reg=5592.377，演化进行到一定阶段后，可以明显看到规律性的波浪出现直至离开，从而出现图7液膜厚度峰值的周期性波动。这也印证了本文所述，气体速度的提高增大了气液相界面的不稳定性和波动性。

图5 Case 3中气液界面随时间的演化

图6 Case 1～3在t=2.5 ms时气液界面状态

图8描述了不同气体速度下在t=25 ms时刻液膜沿预膜板流动的速度，并与液膜入口速度Ul进行比较。可以看出，液膜流动速度在经历轻微增长后沿着板面逐渐下降趋于稳定。这是因为在气液开始相互作用的入口段，液膜受到气流剪切力的作用速度增高，而后期随着液膜不断向后铺展,在流体粘滞力的影响下又逐渐降低。气体速度很大程度影响液膜速度，液膜速度随气体驱动速度的增大而增大。最后本文讨论了气体速度对平均液膜厚度的影响。平均液膜厚度是流体流动的一个重要参数，二维流动中的平均液膜厚度相当于预膜板上的液体持液量，反应液体流量的变化。本文平均液膜厚度定义为H=Q/L,L为液膜板长度，初始时刻Qo=HlL。如图9所示，与本文液膜表面状态相对应，气体雷诺数的增高引起波液膜表面的波浪形变化，计算域内的液膜平均厚度也随之发生相应的波动。可以看出，随着气体速度的升高，液膜的平均厚度随之降低[30]，这是因为在高速气流作用下，相同的时间里液膜会以更快速度向后铺展，减少了液膜在预膜板后段的堆积，因而固定长度段的平均液膜厚度相应降低，这与图8气液间剪切力的增大会促进液膜的流动结论相一致。

图7 Case 1～3中液膜峰值随时间的变化

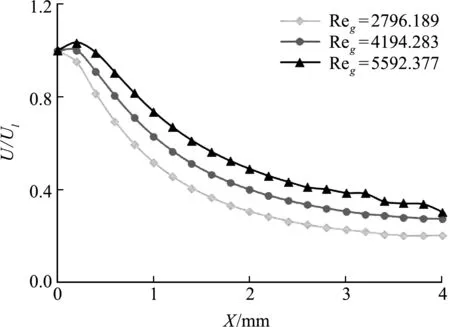
图8 Case 1～3中Reg对液膜流动速度的影响

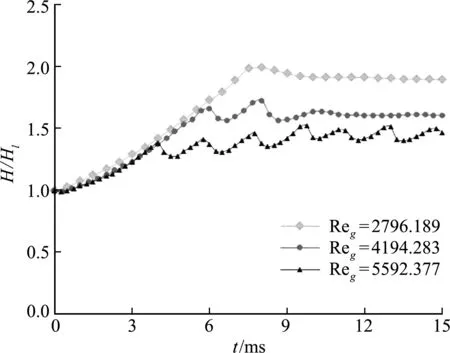
图9 Case 1～3中Reg对平均液膜厚度的影响

5 结 论

本文对Liang等[17]提出的基于相场理论的LBM模型进行修正，通过引入一个额外的界面力来消除两相界面间由于密度变化而导致无法满足体系不可压缩条件的影响，并验证了其实用性。而后使用该模型对于不同气体速度下液膜流动的形态进行模拟，并总结了相应的规律。

(1) 经过修正后的模型能更好地模拟较大密度比条件下的两相流问题，且对于气液相界面变化的捕捉更为准确。

(2) 气体雷诺数增高时，气体驱动液膜在预膜板上的流动速度随之增高，同时会引起气液相界面间出现更大振幅的表面波。

(3) 高雷诺数气体驱动下液膜流动速度较快，因而预膜板上液膜平均厚度降低，液膜堆积现象减弱。