基于state -space -split法的滞回非线性系统随机动力响应分析

徐严钢, 朱海涛*,2, 柳国环, 刘治国,2,3

(1.天津大学 建筑工程学院,天津 300072； 2.天津大学 滨海土木工程结构与安全教育部重点实验室,天津 300072；3.中国市政工程华北设计研究总院有限公司,天津 300074)

1 引 言

自然界中的地震、风和海浪均具有随机动力特性[1]。当激励过大时，工程结构可能会发生局部构件失效，甚至整体破坏，造成巨大的生命和财产损失。因此，研究工程结构在这些随机激励下的动力响应特性，提出工程结构随机动力失效的防护措施，对预防因过大随机激励导致工程结构破坏而引发的危害具有重要科学意义和工程价值。随机激励下的工程结构响应具有随机动力特性，早期研究工作将随机动力荷载等效为静力荷载，近似计算工程结构的动力响应[2,3]。该等效方法计算的结果与实际工况可能会存在较大偏差，从而导致不安全的设计方案。为了获得更准确的计算结果，采用随机振动理论与分析方法是研究工程结构的随机动力响应的一条有效途径。采用随机过程描述随机激励输入，进行工程结构随机响应分析与动力可靠度验算。

另一方面，工程结构在地震、风和海浪等随机激励作用下产生动力响应，可以采用随机振动理论将工程结构简化为随机动力系统进行分析。当随机激励较大时，工程结构动力响应具有几何非线性特性[4]。同时，在能量耗散过程中，也会呈现材料非线性特性。滞回模型是一种描述材料非线性行为的重要模型。在滞回模型的研究中,Bouc-Wen滞回模型得到广泛的研究与应用。该模型由Bouc[5]首次提出，随后Wen[6]进一步完善。Baber等[7，8]研究了其退化现象和Bouc-Wen模型的捏缩效应。

在随机振动分析方法中，最早由Botton[9]提出的等效线性化法应用最为广泛，其主要思想是把随机系统的非线性项进行线性化处理，通过迭代的方法求解出线性化系数，再按照分析线性系统的方法来分析近似后系统的动力响应。许多学者针对等效线性化法进行了改进研究。Caughey[10]通过采用最小方差的原则来确定等效线性化法的参数，同时，对等效线性化法进行了扩展，使其可以运用于多自由度系统的非线性随机振动研究领域。Er[11]在等效线性化法的基础上，提出了SSS(state -space -split)法对系统的FPK 方程进行降维来简化计算。多位学者通过该方法求解了多种随机振动问题。Zhu[12]采用SSS法求解了在高斯白噪声激励下的杜芬形式能量收集器的FPK方程。Er等[13]使用该方法求解了矩形板在高斯白噪声激励下的概率密度函数，并对板不同位置处的挠度概率进行了数值研究。

SSS法的优势在于对高维多自由度复杂激励下非线性随机振动问题的简化计算。该方法可以将高维状态空间中求解FPK方程的问题转化成低维状态空间中求解某些简化FPK方程的问题,且不受系统状态自由度数量和非线性强弱的限制，因此可用于分析大规模非线性系统的概率密度函数解。如Er[11]通过该方法求解了外部激励下的10自由度非线性系统和参数激励下 8自由度非线性系统等。相比Pushover分析，SSS法基于随机振动学，分析复杂结构时，采用电脑模拟出的随机激励，更接近真实情况。Pushover分析法本质是等效静力分析方法，侧向分布力模式的选取十分重要，当研究较为复杂的结构时，水平分布的侧向力并不能完全体现地震的随机动力特性,结果可能会出现偏差。相比非线性时程分析，SSS法前期简化过程简单，损失精度较小，但最终计算结果更依赖于后续方法对简化方程的计算精度。非线性时程法较为成熟，能真实反映结构在地震作用下的破坏机制和构件的塑性破坏过程,但计算过程过于复杂，实际工程中较难推广。

综上所述，针对滞回模型的非线性振动响应以及求解高维非线性问题较有优势的SSS法已开展了一些研究工作。但是，在研究非线性系统的过程中，通常不同时考虑几何非线性和材料非线性对响应的影响。故本文探索性地将Bouc-Wen滞回模型引入杜芬非线性系统，同时考虑非线性系统中的几何非线性和材料非线性，并通过SSS法建立了该非线性系统在高斯白噪声下的联合概率密度函数近似求解方法。

2 引入Bouc-Wen模型的杜芬系统

工程结构的非线性主要包括由于结构几何大变形产生的几何非线性和由于材料的阻尼产生的材料非线性(如滞回特性)。在土木工程领域中，很多构件都具有滞回特性。如RC框架中形成的塑性铰和材料的阻尼等。滞回特性通常可以通过应力-应变曲线来直观表达，带有滞回特性的构件的应力-应变曲线会在加载和卸载的过程中成为一个闭合的滞回环。

本文基于之前研究，以RC框架结构为例，将Bouc-Wen模型引入杜芬非线性系统。其初始状态基于以下几点假设。

(1) 在RC 框架结构的平面振动研究中，将其简化为质点系模型。

(2) 不考虑柱的轴向伸缩，认为楼板的刚度无限大且只做平动运功，各层的质量都集中在楼板上，在地震的激励下楼板和各层框架位移相同。

(3) 柱截面满足平截面假定，横截面在变形前后垂直于中性轴不改变。

(4) 以刚度屈服比未变化的初始瞬时进行分析，首先不考虑材料非线性引起滞回力的参与，求解出剪力后，再将非线性滞回力按刚度屈服比分配进恢复力中，与线性恢复力和几何非线性恢复力共同组成非阻尼恢复力。如图1(a)所示，建立单层单跨的RC框架模型[14],其力学模型如图1(b)所示。

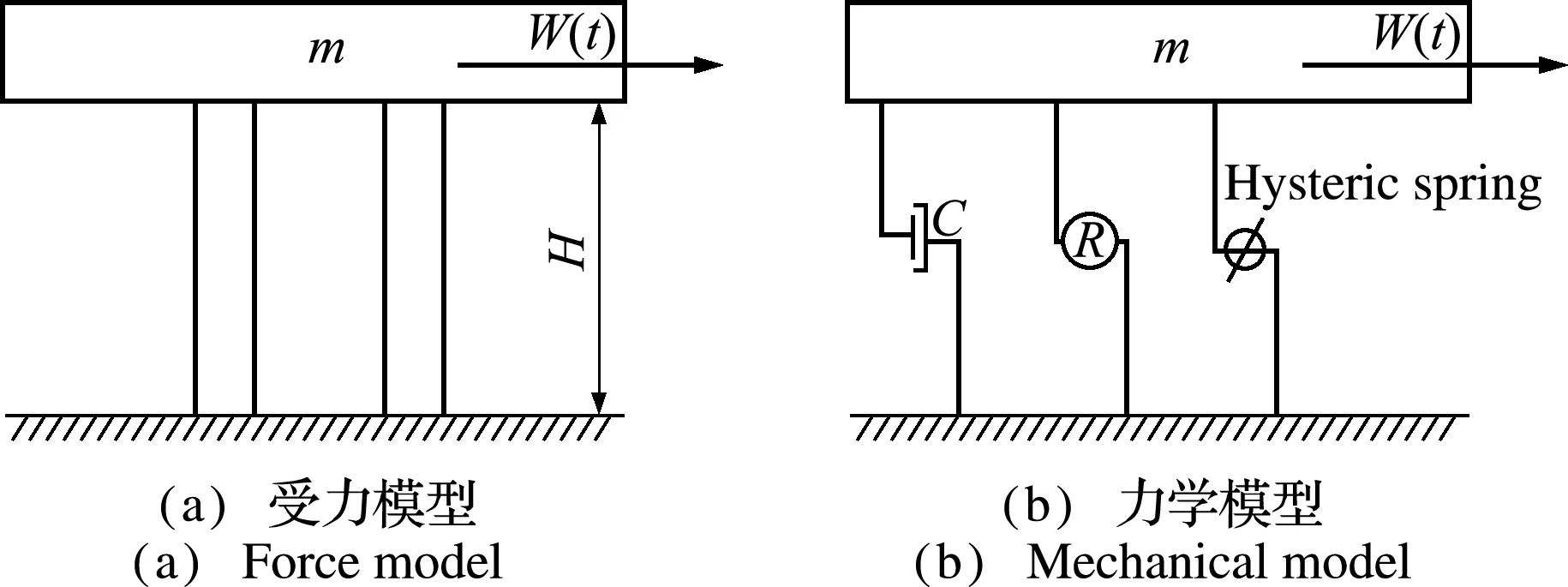
图1 单层框架受力模型及力学模型

假设此模型柱长度为H，抗弯刚度为EI，楼板和梁的质量合为m，滞回环形状控制参数有A，n，β，γ，α∈(0，1)为屈服前后的刚度比，W(t)为地震力，剪力R可表示为[14]

(1)

设此时考虑材料非线性和几何非线性，系统的振动方程如下。

(2)

式中c=2mζ，ζ为阻尼系数。

当W(t)为地震力时，采用高斯白噪声ξ(t)来模拟地震的激励过程。式(12)两侧同除以m，同时考虑经典Bouc-Wen模型(n=1)，则

(3)

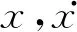
3 等效线性化法

采用等效系统残差均方差最小原则，式(3)的非线性项可以近似为线性项来表示。其等效线性系统如下[15]。

(4)

式中de=3αεE[x2]，ce=βF1+γF2-A，ke=βF3+γF4。参数F1,F2,F3和F4可表示为[7,16]

(5,6)

(7)

(8，9)

(10)

4 State -Space -Split法

将

和z=x3代入式(3)，则原式的一阶微分方程组如下：

(11)

此非线性动力系统对应的平稳响应的 FPK 为

(12)

式中p代表p(x1,x2,x3,t)。根据SSS法，对式(12)在x3的域内积分有

(13)

式中p为p(x1,x2)。其中，q(x3|x1,x2)可以通过等效线性化法来得到其近似解。

(14)

方差为

(15)

通过SSS法降维后的FPK方程如式(16)所示。其精确解可直接求得。

(16)

(17)

式中K为第二类修正Bessel函数。

D=2ξω+(1-α)ω23(σ3/σ2)

(18)

(19)

(20)

随后x1,x2和x3的近似联合概率密度函数可以通过降维后的二维FPK方程精确解和近似条件概率密度函数近似表达：

p(x1,x2)

(21)

5 数值分析

分析非线性模型在均值为0的高斯白噪声激励下响应的概率密度函数。选取三个例子以及一个实体工程进行讨论，验证所提方法的适用性。非线性模型的方程见式(3)。参数取值如下,ω=1,ξ=0.05,α=0.5,β=0.5,γ=-0.5,n=1和A=1。

表1 系统参数

采用蒙特卡洛模拟结果对比验证SSS法的准确性，并与等效线性化法所求得的结果进行比较，证明其优越性。计算结果如图2～图4所示。其中蒙特卡洛法产生的样本数为1000万。由SSS法、等效线性化法和蒙特卡洛法求解的结果分别简写为SSS，EQL和MCS。概率密度函数简写为PDF。

算例1的结果如图2所示。图2(a,e)表明激励强度和非线性系数均较低时，在位移PDF的峰值区域和尾部区域，相比EQL，SSS和MCS的拟合程度更好。表明此条件下的位移PDF是非高斯分布的。图2(b,f)是速度PDF图。对于速度PDF，SSS和EQL结果相同。对于峰值区域，两者均存在偏差；对于尾部区域，两者精确度都较好。图2(c,g)为滞回力PDF分布。对于峰值区域，SSS和EQL均存在少量误差，不能精确地描述峰值区域；对于尾部区域，SSS和MCS存在少量误差，误差小于EQL。这证明了在激励强度和非线性系数较低时，相对EQL法，SSS法可以更好地描述位移和滞回力的PDF，尤其是尾部区域。图2(d，h)为算例1的位移-速度联合分布。从位移方向来看，在[-0.5,0.5]区间内，EQL结果略大于SSS的结果。而在[-0.5,0.5]区间外，SSS的结果分布更宽于EQL的结果，分布趋势近似于位移PDF的趋势。

图2 算例1概率密度函数的分布

算例2的结果如图3所示。如图3(a,e)所示，保持几何非线性系数不变，增大激励，对于位移PDF，EQL和MCS的误差增大，而SSS和MCS的拟合依然良好。随着激励的增大，位移PDF逐渐远离高斯分布，且EQL法精度降低。图3(b,f)表明，EQL和SSS依然相同且精度较高,精度不受激励影响。图3(c,g)为滞回力的PDF。对于峰值区域，两种结果都和MCS存在误差，EQL的误差较小；但对于尾部，SSS误差更小。激励增大后，SSS法能较好地描述滞回力PDF的尾部区域。图3(d,h)为算例2的位移-速度联合分布。从位移方向来看，在[-1,1]区间内,EQL大于SSS；在[-1,1]区间外，SSS分布比EQL广泛。激励增大导致联合分布的范围变得更广,峰值降低。

图3 算例2概率密度函数的分布

算例3结果如图4所示，保持激励大小不变，增大非线性系数。如图4(a,e)所示，对于位移PDF，SSS和MCS拟合较好，而EQL误差偏大。在非线性系数和激励均较大时，EQL法精度明显降低。图4(b,f)是速度PDF，三者几乎重合，速度PDF呈高斯分布。图4(c,g)为滞回力PDF，对于峰值区域，EQL误差偏小；而对于尾部，EQL存在着较大的误差，SSS能保持较高的拟合精度。图4(d,h)为算例3的位移-速度联合分布。其趋势与 图3(d,h)相似。在峰值处，EQL和SSS结果相差更大。这与算例2和算例3的位移PDF分布的差异情况相似。

采用SSS法和蒙特卡洛法，通过首超破坏机制中的单侧安全界限机制和破坏准则，计算一榀单层混凝土框架结构在平稳高斯白噪声激励下的可靠度,验证其实用性。取激励强度S0=0.002 m2/s3，结构自振频率为w0=12 rad/s，阻尼比ζ=0.05，高度H=13.2 m，ε=6.198。Bouc-Wen模型的参数采用刘俊等[17]通过参数识别所获得的模型参数，α=0.2,β=0.202,γ=0.3147,n=1,A=1.1037，单侧安全界限b=2.4 cm。结构动力可靠度公式如下。

(22)

从图5可以看出，当t=9 s时，响应达到平稳。从图6可以看出，SSS法计算结果与MCS结果几乎吻合，证明了该方法准确度接近数值模拟结果，在工程上可行。

图4 算例3概率密度函数的分布

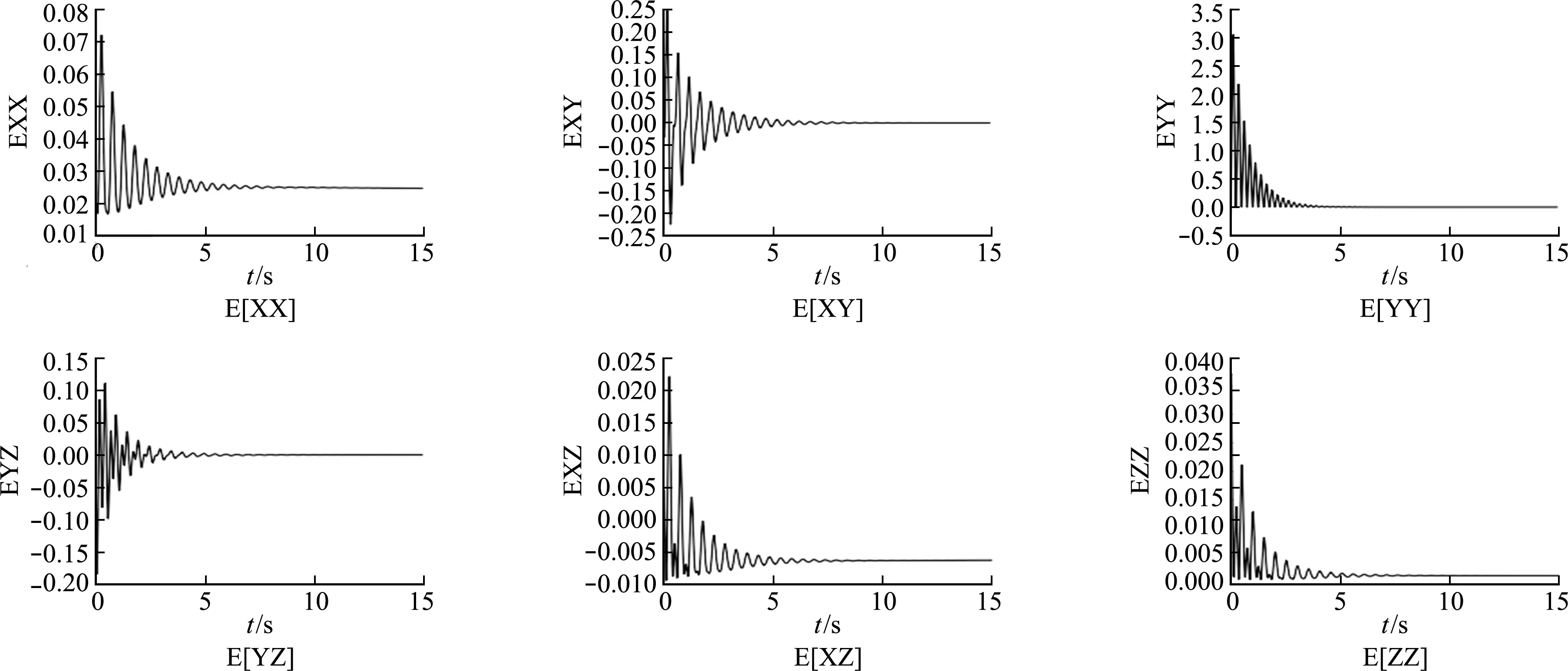
图5 二阶矩变化曲线

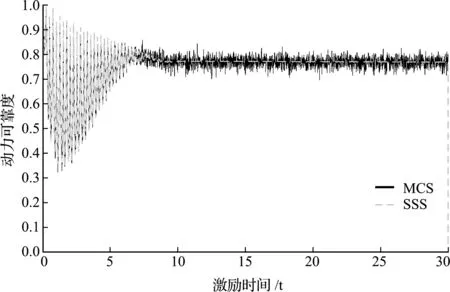
图6 动力可靠度变化

6 结 论

采用SSS法分析了一类同时拥有几何非线性和材料非线性的非线性随机动力系统的响应，获得了系统在高斯白噪声激励下平稳响应的概率密度函数，并通过实例验证了其有效性。研究表明，

(1) 在求解位移PDF 时，当激励较小时，SSS法和EQL法对峰值区域求解精度较高。对于尾部区域，激励增大后，EQL法求解会产生较大误差而SSS法能保持较高的求解精度。

(2) 求解速度PDF时，SSS法和EQL法计算的结果相同，且速度概率密度函数分布始终保持近似高斯分布。

(3) 求解滞回力PDF时，在峰值区域，随激励增大，两种方法都不能很好地对PDF进行描述。对于PDF的尾部，SSS法的求解精确度更好。工程结构的破坏往往和PDF尾部关系比较紧密，因此分析PDF尾部分布有重要意义。SSS法在分析这类非线性模型随机振动问题时，可以提供更精准的概率密度函数解。

(4) 当几何非线性系数增大时，EQL求解的误差会增大，而SSS法可以保持较高的精度。

(5) 本文主要研究 SSS法求解复杂非线性滞回模型在均值为零的高斯白噪声激励下平稳响应的可行性和适用性。但对于地震作用下的桥梁等土木建筑结构，更多采用过滤白噪声或考虑非平稳过程。当考虑过滤白噪声激励时，需在原振动方程组中增加一滤波器方程，得到相应的FPK方程，再采用SSS法进行降维运算。关于SSS法的详细降维运算过程可参见文献[11]。对于非平稳过程，SSS法需要进一步研究，使该方法可以拓展解决非平稳问题。