基于变密度法的平模台振加强筋布局优化

蔡安江，杨奇琦

(西安建筑科技大学 机电工程学院，西安 710055)

1 引 言

平模台振因生产效率高且生产预制构件种类多而成为装配式建筑生产线的重要设备，但是普遍存在振动台面刚度不足和振动能量利用率较低等问题，导致振动效果不理想，混凝土预制构件成型质量差。为了解决上述问题，振动台面常采用加强筋结构，既能为平模台振各部件提供安装位置，又能提高振动台面刚度，改善振动台面动力学传递特性[1,2]，使设备运行平稳、噪声降低、能量利用率提高，从而提升平模台振的振动效果和混凝土预制构件成型质量。因此，研究振动台面加强筋布局优化对于提高平模台振的振动效果具有重要意义。

随着拓扑优化技术的不断成熟，国内外学者关于加筋板壳结构的优化进行了大量研究工作。Tamijani等[3]采用伽辽金法对加筋板结构进行了分析，建立了Kriging代理模型，并利用遗传算法优化加筋板结构的尺寸和形状，结果表明，采用无网格法可在保持板的几何形状和网格尺寸不变的情况下对每个设计点重新生成加强筋，大幅度缩短了计算时间。Xiang等[4]采用仿生设计方法对加筋工作台的结构进行拓扑优化，与传统设计相比，优化后的仿生结构变形量和重量减小，固有频率提高，工作台力学性能明显提升。Li等[5]研究了薄板结构在简谐激振力作用下的加强筋布置问题，利用植物叶脉的自适应生长机制，提出一种以指定位置的位移响应幅值最小为目标的进化算法，实现了连续体结构的刚度优化设计。崔荣华等[6]研究了不同边界条件下薄板的加强筋分布优化，根据加筋板结构各部分抗弯刚度的差异，建立等效刚度模型，基于水平集法得到了加强筋的最优分布。刘海等[7]基于变密度法进行加强筋布局优化来实现加筋箱体结构降噪设计，利用移动渐近线(MMA)寻优算法确定了加强筋的位置，取得了良好的降噪效果。李蕾等[8]提出了平板加强筋生长设计方法，利用单元灵敏度决定结构中加强筋的保留或去除，获得了多种边界条件下平板加强筋的最优布局。

振动台面结构设计时，台面的刚度和强度等力学性必须满足预制构件最佳成型质量的需求，并且要考虑各组成部件安装位置的合理性，以使平模台振达到理想的振动效果。振动台面结构设计不合理将无法生产满足强度要求的预制构件，因此振动台面的优化设计非常必要。目前，振动台面结构单一且存在很多局限性，其设计大多依赖工程人员的主观经验，缺乏类似的振动台面优化设计工作。本文以提升平模台振设备的振动效果为目标，基于变密度法对振动台面加强筋的布局进行了拓扑优化。

2 优化问题分析

平模台振系统模型如图1所示，系统主要由振动台面、底座和激振器组成。振动台面由矩形钢板和加强筋两部分焊接而成，并有12个橡胶弹簧支撑，振动台面两侧共安装8个激振器提供激振力，激振力通过侧板传递到台面，再由台面传递给混凝土预制构件，为预制构件提供振动能量并完成密实成型。

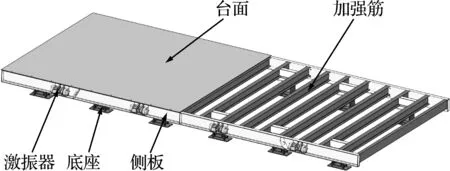
图1 平模台振系统模型

平模台振力学模型如图2所示，激振器对称分布在振动台面两侧，偏心块做同步反向旋转运动产生离心惯性力，惯性力沿x方向分力相互抵消，沿z方向分力叠加形成激振力，驱动振动台面沿z方向作简谐振动。

振动台面总激振力为

(1)

式中Fr(x,y,t)为第r个激振器提供的激振力,m0为偏心块质量,ω为偏心块角速度,t为时间。

平模台振工作状态是动态非线性的，振动台面承受的载荷也具有复杂的非线性[9]，而拓扑优化方法难以对动态非线性过程建立准确的数学模型。考虑到若振动台面在最大载荷工况下能满足平模台振的工作需求，则在其他工况下也能满足工作需求。所以，进行拓扑优化时选取载荷最大的工况进行分析，即振动台面所受激振力最大。在此工况下，每个激振点处的激振力幅值为18 kN，且需约束振动台面沿x和y方向的移动自由度及z方向的转动自由度，振动台面底部支承点处施加弹簧约束模拟橡胶弹簧底座。

目前，振动台面加强筋大多采用如图3所示的布局，加强筋等间距并排布置在台面底部。其优点在于加强筋的布置形式简单，简化了振动台面的设计及制造，并且载荷能够均匀分配到每个加强筋。这种振动台面以总质量最小为设计目标，以加强筋间距为设计变量，加强筋数量与振动台面总质量的关系如图4所示。可以看出，随着加强筋数量的增加，振动台面总质量逐渐减小，直至矩形钢板达到最小厚度。即存在最优的加强筋数量，使得振动台面实现轻量化设计目标。虽然此振动台面结构已用于实际生产，但是其存在一定的局限性，如振动台面整体刚度不足和振动能量传递效率低等。

图2 平模台振力学模型

3 振动台面的优化设计

3.1 拓扑优化数学模型

拓扑优化的基本思想是在给定载荷及边界条件下，在设计空间中寻找材料最优分布形式[10-12]。与传统优化设计不同的是，拓扑优化只需给出结构参数(材料特性、载荷和边界条件)和材料去除体积比[13-15]。

本文优化问题实际上是材料分布状态0～1优化问题，即确定振动台面基结构材料的有(表示为1)与无(表示为0)，最终生成加强筋布局的设计方案。采用基于SIMP材料插值模型的拓扑优化方法[16]，得到具有可变刚度的各向同性材料，将材料相对体积密度x(x在0～1之间连续变化)作为设计变量分配给设计空间的每个有限单元，该密度可直接影响单元刚度矩阵。为了消除没有物理意义的中间密度，在设计变量中加入惩罚因子，迫使设计变量趋向于极值0或1，以生成更离散的结构。

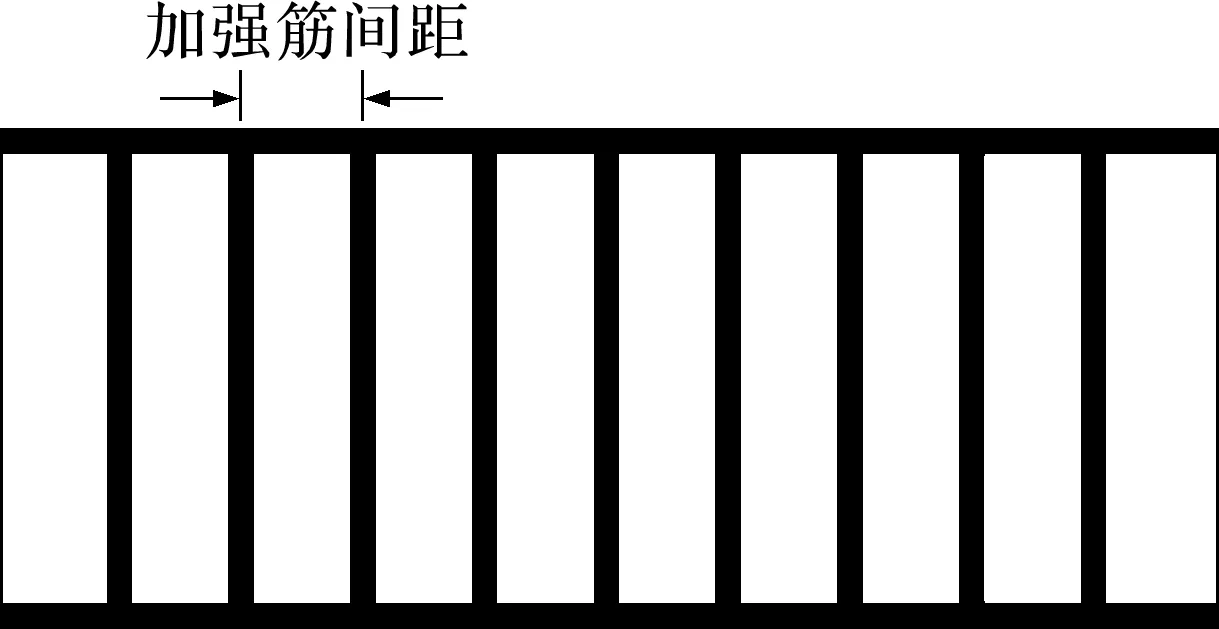
图3 振动台面加强筋的布局

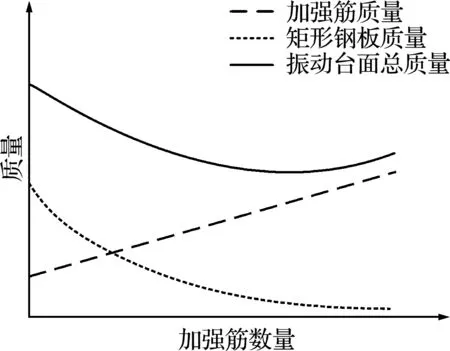
图4 加强筋数量与振动台面总质量的关系

SIMP材料插值模型如下：

(2)

式中Ke为e号单元优化后刚度矩阵，K0为e号单元初始刚度矩阵，xe为e号单元的相对密度，p为中间密度惩罚因子，取p=3。xe的取值区间为[0,1]，当xe取0时表示该单元材料缺失，当xe取1时表示该单元充满材料。为了避免刚度矩阵的奇异性，通常将单元相对密度下限xmin限制为很小的值。

以振动台面结构的刚度最大即柔度最小为优化目标，以单元相对密度作为设计变量，以体积分数为约束条件，建立拓扑优化数学模型如下：

(3)

式中x为单元相对密度向量，C为结构总体柔度，F为结构载荷向量，U为结构位移向量，K为结构总体刚度矩阵，V为结构优化后体积，f为保留体积比，V0为结构设计域体积，ve为e号单元的体积，xmin为单元密度下限，取xmin=0.001，xmax为单元密度上限。

对拓扑优化问题进行灵敏度分析，将目标函数相对于设计变量求导为

(4)

利用伴随方法[17]，可得到以下结果

(5)

将SIMP材料插值模型引入到式(5)，得到结构总柔度相对设计变量的灵敏度为

(6)

式中Ue为单元位移向量。

获得灵敏度结果后，在求解优化模型时采用最优准则法，基于KKT(Karush Kuhn Tucker)条件得到拓扑优化模型(3)最优性条件表示为

(e=1，2，…，n)(7)

式中λ为拉格朗日乘子。本文载荷为设计独立载荷，∂C/∂xe<0。式(7)可改写为

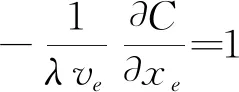
(e=1，2，…，n)(8)

为了控制移动步长和确保迭代稳定，引入步长因子ξ和阻尼因子δ，ξ和δ在区间[0,1]内取值。由此可构造设计变量的迭代公式为

(9)

i为迭代步数。

根据KKT条件可知，最优解处的约束转化为等式约束，将迭代公式代入取等号的体积约束中，可获得关于λ的非线性代数方程，使用二分法便可得到拉格朗日乘子λ。

3.2 拓扑优化有限元模型的建立

有限元软件ANSYS Workbench的Topology Optimization拓扑优化模块使用的技术是基于变密度方法的，利用该模块进行拓扑优化的流程为,定义材料属性，导入几何模型；划分基结构网格，施加约束及载荷；设置拓扑优化参数，计算求解。

在结构拓扑优化之前，首先需要确定设计空间及非设计空间。如图5所示，设计空间为加强筋分布区域，此空间的材料需要部分去除；而非设计空间则是矩形钢板区域，此空间结构特征保持不变。加强筋分布区域厚度为200 mm，矩形钢板区域厚度为10 mm，拓扑优化过程中需要从厚度为210 mm的基结构中去除设计空间的多余材料，生成加强筋材料的分布形式。

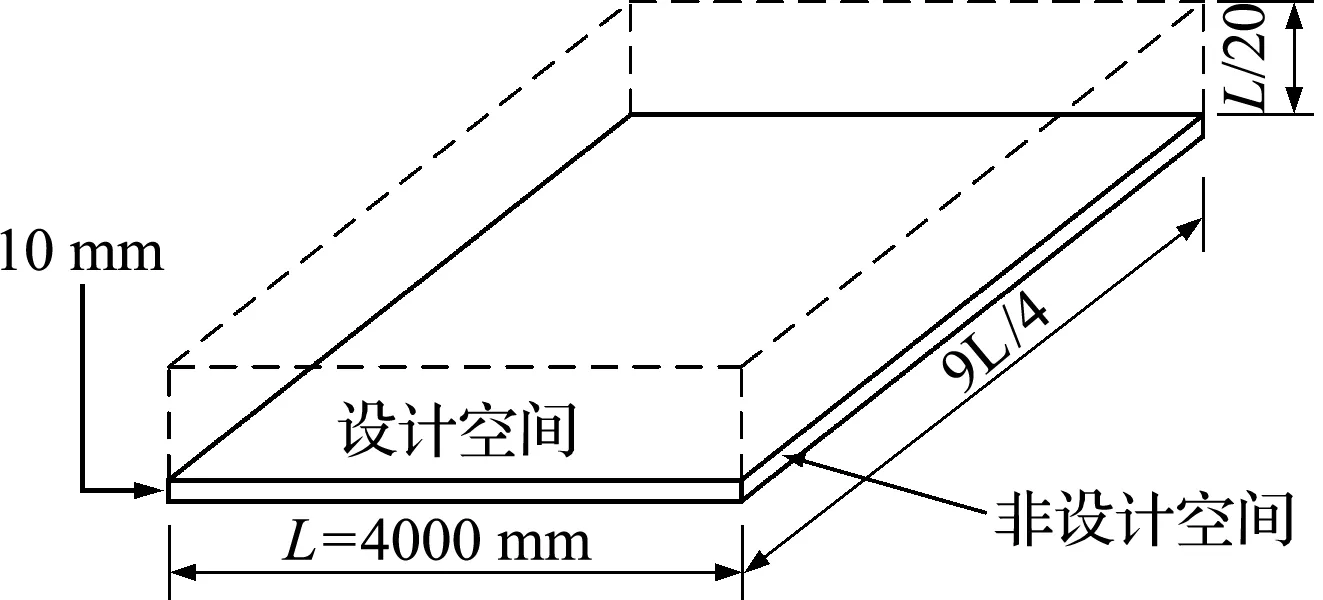
图5 振动台面设计空间及非设计空间

振动台面基结构有限元模型如图6所示，台面和加强筋材料均为Q235，主要材料参数为,弹性模量E=2×1011Pa，泊松比ν=0.3，密度ρ=7850 kg/m3。采用六面体单元对基结构进行网格划分，网格划分过程中沿基结构厚度方向划分较为密集，划分为4层网格。基结构有限元模型共72376个单元，293738个节点。

3.3 体积分数的影响

体积分数(VF)是拓扑优化的重要参数，在某些情况下可直接通过最终设计质量确定体积分数。本文振动台面原结构中加强筋质量(2692 kg)与设计空间质量(56112 kg)相比非常小，导致体积分数小于5%。Rozvany[18]指出过低的体积分数不能用于密度拓扑优化，通常采用较高的体积分数。此外，设计空间的体积分数响应不能直接代表最终设计，因为没有考虑到应用不同截面加强筋来实现同样的功能，同时加强筋的结构特点也会导致体积分数非常小。

选取体积分数在5%～30%之间的拓扑优化结果进行对比分析，如图7所示。图中黑色为需要删除材料的区域，相对密度接近0；灰色为需要保留材料的区域，相对密度接近1。通过比较不同体积分数的拓扑优化结果可以确定振动台面最佳传力路径，指导加强筋的重新布局，最终生成可行的设计方案。可以看出，在台面宽度方向上需要分布若干加强筋；但是对于不同的体积分数，台面长度方向上材料分布有所差异，低体积分数不像高体积分数材料分布清晰稳定，这是体积分数过低导致的。此外，所有拓扑优化结果为对称形状，原因是拓扑优化设计中存在对称性约束，即结构对称面上指向边界的位移自由度和绕边界的转动自由度受到约束。加强筋在尺寸调整和位置确定之前，其真实性能仍是未知的，因此进行加强筋布局的优化研究时，体积分数是一个需要研究的重要参数。

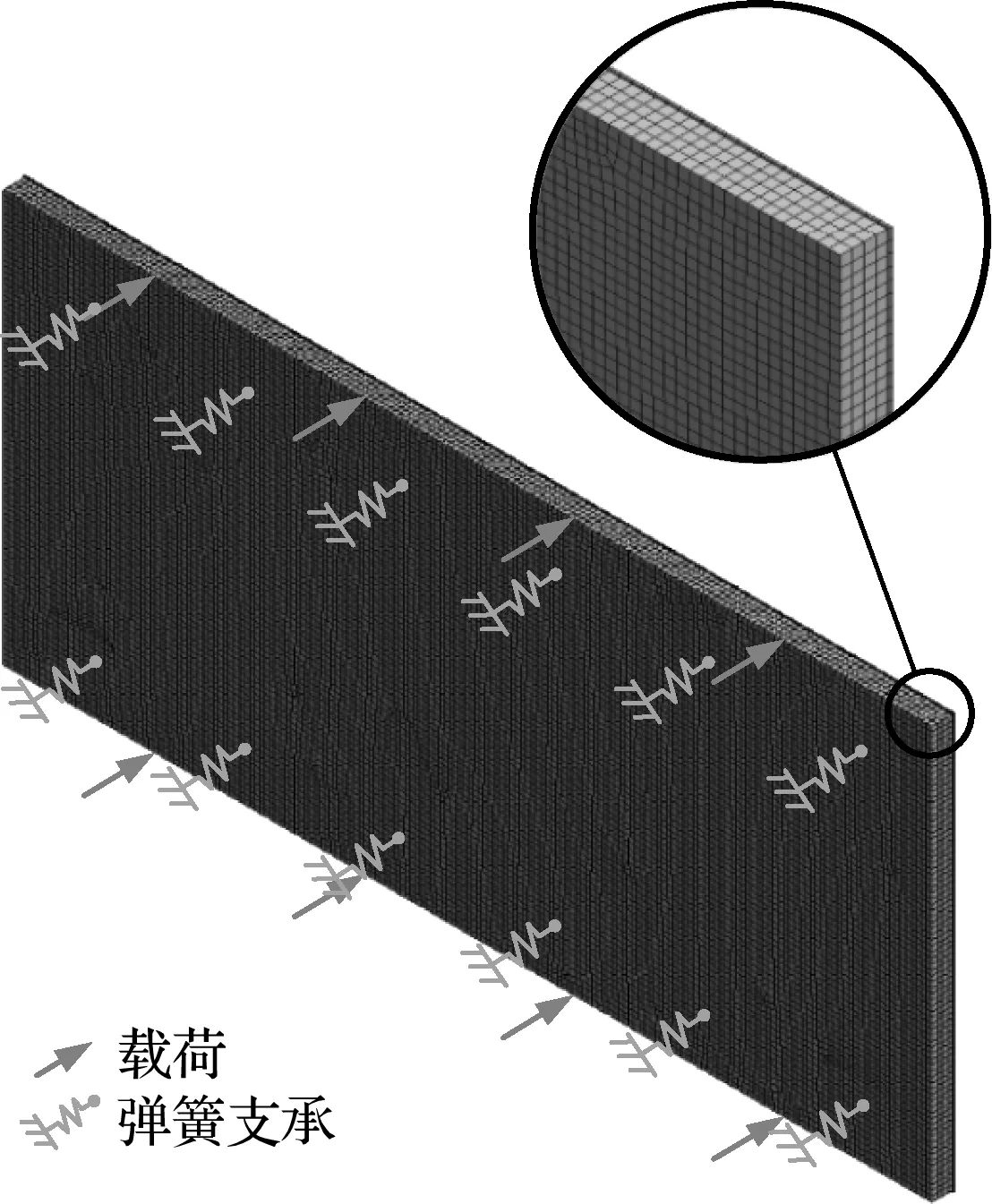
图6 振动台面基结构有限元模型

图7 不同体积分数的拓扑优化结果

3.4 振动台面的结构设计

依据拓扑优化结果能够确定加强筋位置，但不能确定加强筋具体的尺寸参数和截面形状，故直接使用矩形梁单元代替材料分布区域是不正确的。通过查看拓扑优化结果，材料分布区域的截面形状与工字钢的截面形状较为吻合，且工字钢具有质量小、刚度大等优点，因此选取不同型号的工字钢作为振动台面的加强筋。

振动台面加强筋布局设计方案如图8所示，综合考虑振动台面的强度、刚度及制造成本，在制定设计方案时选取体积分数为30%。根据拓扑优化结果，在材料保留区域设置工字钢生成新的设计方案，并通过有限元软件测试，进一步提升振动台面的力学性能。此外，为了便于振动台面的制造以及满足批量生产的需要，在符合结构优化结果的基础上将加强筋设计为规则的轴对称布局。

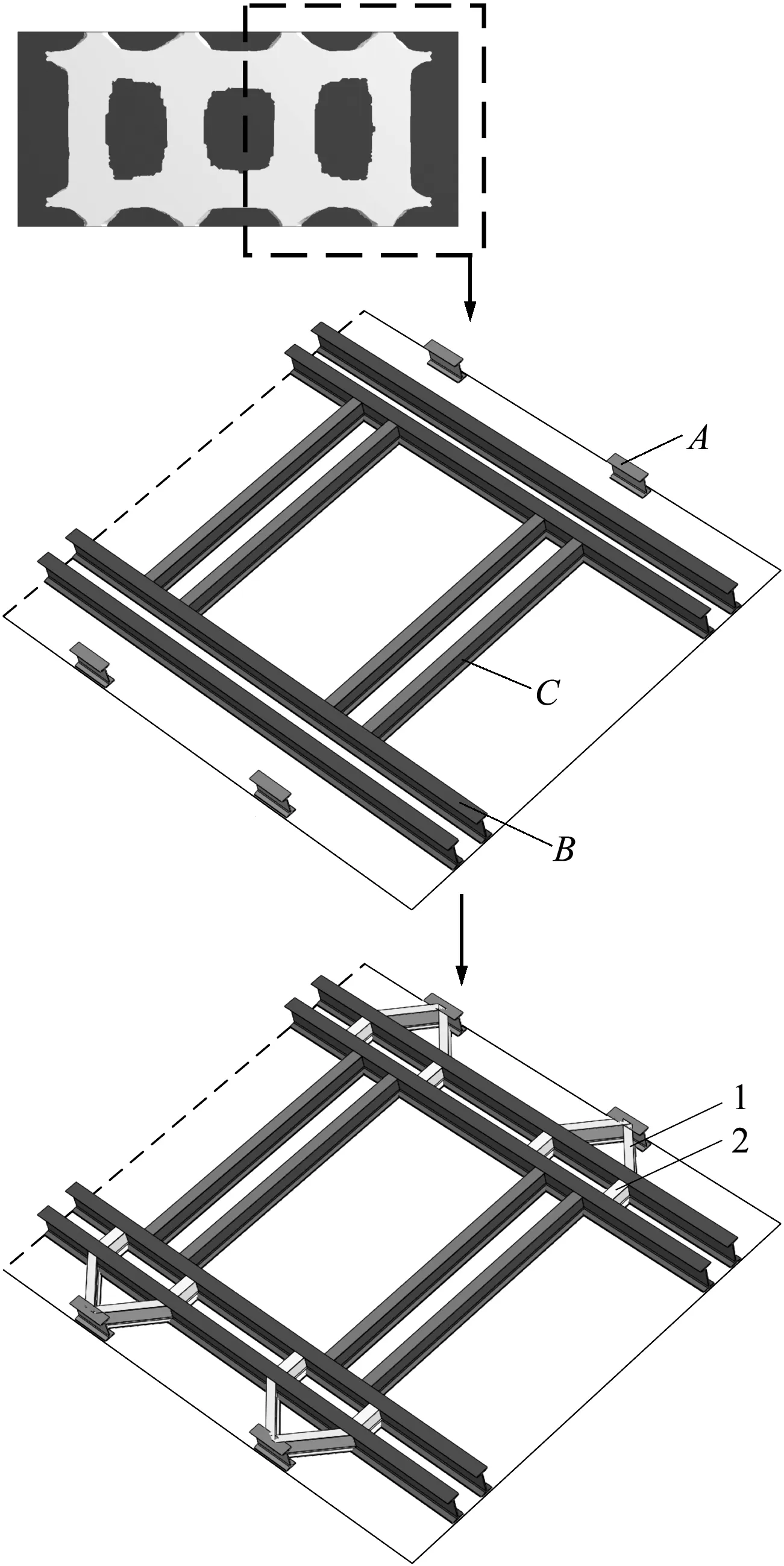
图8 加强筋布局设计方案

设计方案中，工字钢A的腹板处用来安装激振器，工字钢B和C的作用为组成模台框架，增大台面刚度和防止振动台面发生挠曲。考虑到振动台面纵向尺寸较大，将其长度方向上的加强筋由原结构的单工字钢增加为双工字钢共同承受负载。振动台面宽度方向上，加强筋由原结构的等距分布改变为需要加强部位的非等距分布。二次加强筋1和2用来连接主要加强筋，加固振动台面边缘以及传递激振能量。工字钢B的型号为25b，其余工字钢型号均为20a。

优化后振动台面模型如图9所示，振动台面总质量由原来的5878 kg变为5555 kg，减重323 kg，实现了结构轻量化设计。

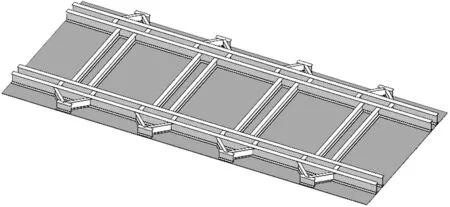
图9 优化后振动台面模型

4 振动台面的性能评估

利用有限元软件对优化后的结构进行模态分析和谐响应分析，测试振动台面力学性能及平模台振振动效果。

4.1 模态分析

通过ANSYS Workbench的Modal模块，计算得到振动台面前8阶振型如图10所示，振动台面前10阶固有频率列入表1。为了方便对比，将原结构和优化结构的前10阶固有频率一并列入 表1。可以看出，优化后振动台面的固有频率明显提高，增幅在4.46%～32.71%。

图10 优化后振动台面前8阶振型

4.2 谐响应分析

在实际工况中，平模台振长时间处于周期振动状态下工作，进行谐响应分析能真实地反映振动台面在工作中的力学性能。通过求解计算，得到优化前后振动台面在工作频率50 Hz时的应力分布云图及位移云图如图11和图12所示。

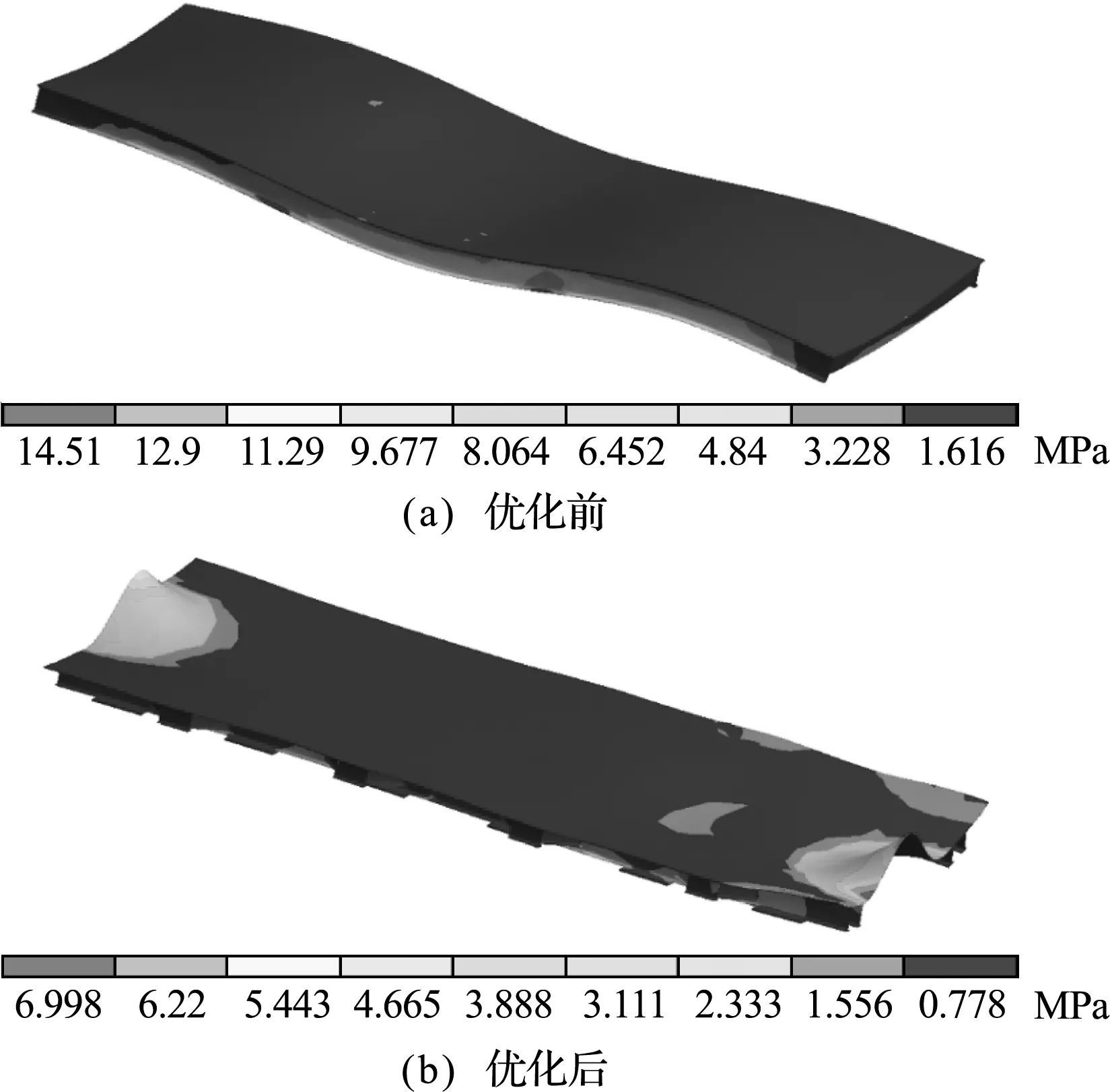
图11 振动台面应力分布云图

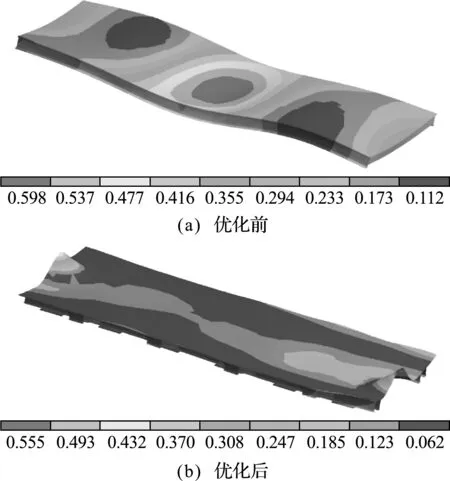
图12 振动台面位移云图

对比发现，振动台面强度提高，原结构的最大应力为 14.51 M Pa，优化结构的最大应力为 6.998 M Pa，比优化前降低了51.77%；振动台面整体刚度提高，原结构的最大位移量为0.598 mm，优化结构的最大位移量为0.555 mm。而且优化前最大变形出现在振动台面中部，对预制构件的成型质量会产生较大影响，优化后最大变形在振动台面短边边缘处，可通过焊接角钢的方法避免变形出现。

综上所述，优化后振动台面的各阶固有频率避开了工作频率50 Hz，有效避免了共振发生，防止了平模台振设备损坏；优化后振动台面可显著提高强度和刚度，从而提高了平模台振设备的振动效果。

5 结 论

(1) 振动台面作为平模台振设备的关键部件，在工作中反复承受高频简谐载荷，其加强筋布局对平模台振振动效果及混凝土预制构件成型质量有着重要影响。

(2) 提出了利用变密度拓扑优化方法改进平模台振振动台面加强筋布局的方法，进行了结构总柔度相对于设计变量的灵敏度分析，采用最优准则法对拓扑优化模型进行求解。根据拓扑优化结果得到优化后的振动台面，其力学性能显著提高，并且实现了结构轻量化。

(3) 采用优化后振动台面的平模台振可有效提高振动效果，很好满足了平模台振的性能要求。验证了基于变密度法的振动台面加强筋布局优化的可行性，对工程实际中平模台振的设计具有一定指导意义。