求解大柔度梁/绳索的ANCF单元及隐式迭代格式

罗 鑫，魏泳涛

(1.四川大学 建筑与环境学院，成都 610065; 2.四川中锐信息技术有限公司，成都 610094)

1 引 言

绳索结构应用广泛，如太空中的系留卫星系统(Tethered Satellites System)[1,2]、海洋船舶工业、核工业和机场等领域内的桥式起重机(Overhead Cranes)[3,4]以及高速列车系统中的悬链线(Pantograph/Cantenary)[5]等。弹簧-阻尼-集中质量模型[6-8]是数值模拟绳索的常用方法，但该法的绳索处理成分段折线而不再保持光滑曲线的形态，因而精度较低。有限元法在分析绳索时[9,10]，通常采用具有极低抗弯刚度或大柔度的梁单元以保证其形态的光滑性。在绳索运动中，往往存在大范围刚体运动和大变形的耦合作用。但传统梁单元的节点自由度仅反映变形的挠度和转角，即单元的刚体运动和变形是解耦的。浮动坐标法[11]将绳索运动考虑成随浮动坐标系的大范围运动与相对于浮动坐标系的变形的叠加，但由此导出的科氏力和向心力等惯性力表达式十分复杂。

为克服浮动坐标法中的难点，Shabana[12]提出了以节点坐标和斜率作为节点自由度的绝对节点坐标方法ANCF(Absolute nodal coordinate formulation)。该方法的基本思想为在连续介质力学中对即时构形进行物质描述时，运动和变形本身就是耦合的。因此，若将梁/绳索的节点坐标和斜率而非节点挠度和转角设置为节点自由度，则可自动耦合大范围运动和大变形，也无需单独考虑科氏力和向心力等惯性力，且质量矩阵是常数矩阵。 ANCF 已有关于绳索的研究，Gerstmayr等[13]将标准梁单元的自由度减少并引入附加的形函数，构造了低阶的空间两节点绳索单元；Seo等[14]使用该单元模拟了高速列车系统接触网的三维大变形问题；Shan等[15]使用无抗弯刚度的该单元分析了太空中的系留网。

ANCF中单元的节点等效力计算远比传统有限元复杂。刘铖等[16]基于第一类Piola-Kirchhoff应力张量导出了节点等效力及雅可比矩阵的解析表达式。范纪华等[17]在节点等效力求解中引入了弹性线方法。Gerstmayr等[13]逐一计算了节点等效力各元素，特别是对应于弯曲变形的情况。Zemljaric等[18]对节点等效力计算方法进行了一定简化。Berzeri等[19]推导了小变形下欧拉-伯努利梁单元的节点等效力。这也是目前ANCF分析绳索时采用显式积分的主要原因。显式积分不需要迭代，既避免了不收敛的问题，也免去了由节点等效力导出切线刚度矩阵的繁琐过程，但必须按算法的稳定原则确定足够小的时间步长。而隐式积分在各时间步上需迭代求解以满足平衡方程，在采用较大时间步长时也能保证精度要求。

由节点等效力导出隐式积分所需的的切线刚度矩阵，目前尚无此方面完整研究的报道。此外，基于ANCF方法分析绳索时，多针对单根绳索，而对工程中常见的多根绳索系于一点的情况，还未有考虑。本文对ANCF大柔度梁/绳索单元，导出了用于平衡迭代的切线刚度矩阵的全部公式；其关键环节在于将两矢量的叉乘表示为反对称矩阵与矢量的点乘，以此改造ANCF大柔度梁/绳索单元的节点等效力公式；由此导出的节点等效力和切线刚度矩阵均为矩阵形式，也非常方便代码开发；对不同ANCF单元的铰接和刚性连接，引入罚方法的处理；最后结合HHT(Hilber-Hughes-Taylor)隐式格式，对弦微幅和小幅振动、双杆摆和T字形杆以及柔绳进行了数值模拟。

2 基于ANCF的大柔度梁/绳索单元

研究细长的等截面大柔度梁/绳索，在运动/变形中始终维持光滑曲线，且横截面是正多边形，即横截面对通过形心的任何轴都具有相同的惯性矩。本文基于文献[13]提出的2节点12自由度的ANCF梁/绳索单元，该单元服从平截面假设，不考虑剪切变形和扭转变形。当单元具有极低或零抗弯刚度时，即可用于绳索模拟。

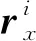
r=[S1IS2IS3IS4I]e=Se

(1)

式中I为3×3的单位阵,S1～S4为埃尔米特插值基函数,e为将节点i和j处的位置矢量和切线矢量排列而得的单元自由度向量。

(2)

Sx,Sx x,rx和rx x为相应的一阶和二阶导数。

单元惯性力在虚位移δr上的虚功为

(3)

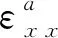
(4)

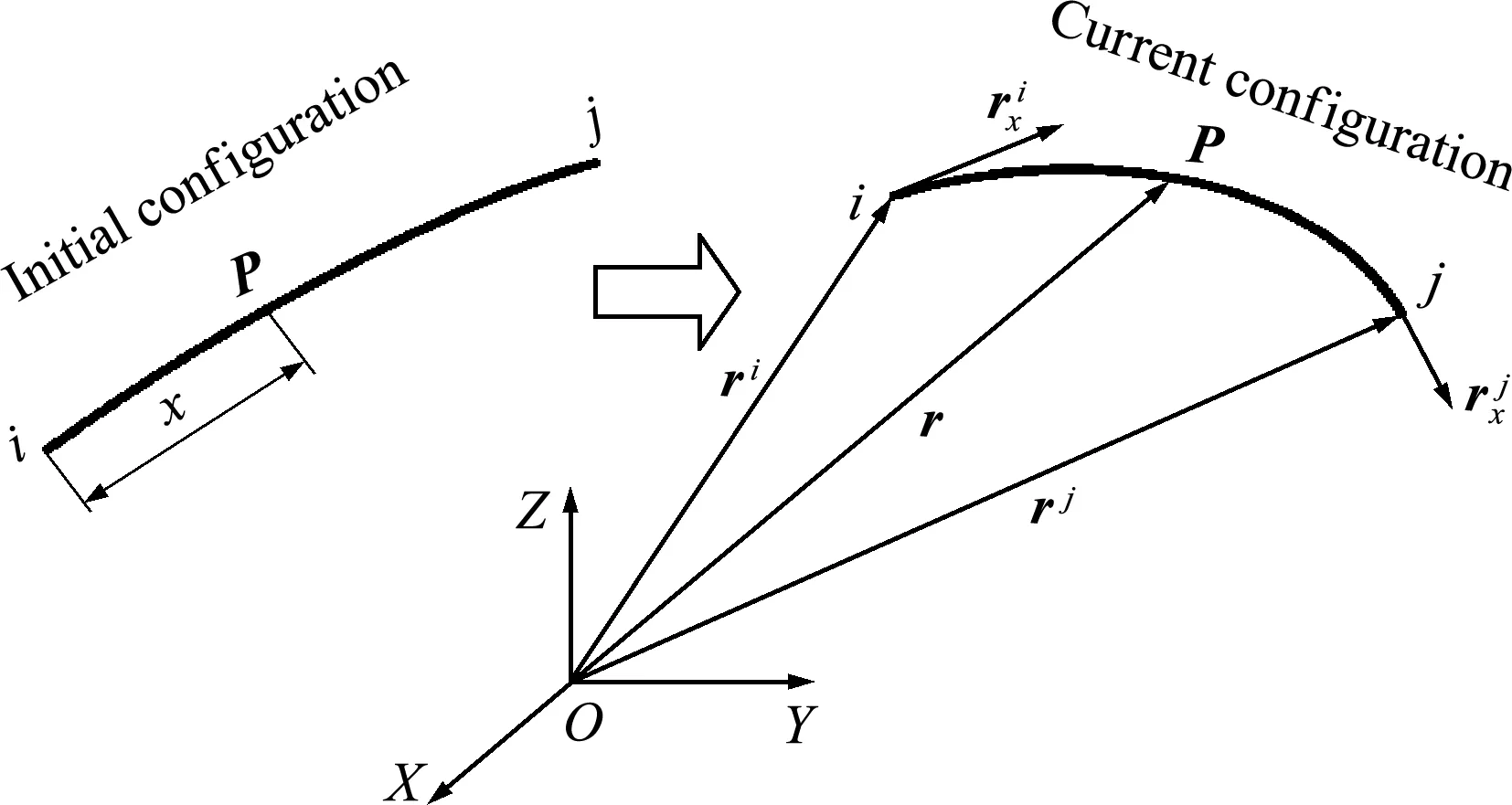
图1 单元内任一点P的位置的插值

由欧拉-伯努利梁理论，单元内力的虚功为

(5)

为简化书写，记矢量c=rx×rx x。将矢量叉乘运算改写为矩阵乘积： -rx x×rx=Grx,rx×rx x=Qrx x,c×rx=Rrx;G,Q和R为反对称矩阵，对偶矢量分别为-rx x,rx和c。

(6)

(7)

(8)

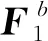
3 隐式动力学迭代格式

为将隐式积分格式应用于前述建立的ANCF大柔度梁/绳索单元，需建立平衡迭代格式，为此应从节点等效力导出相应的切线刚度矩阵。

采用HHT隐式时间积分方法建立绳索的隐式动力学迭代格式，根据HHT方法，

(1+α)Ft + Δt-αFt-Pt + (1 + α)Δt=0

(9)

(10)

(11)

式中Ψ为不平衡力向量，C为阻尼矩阵，P为等效外载荷。

当积分参数满足-0.3≤α≤0，β=0.25(1-α)2，γ=0.5-α时，HHT方法是无条件稳定的。其中α=0时，HHT退化成β=0.25，γ=0.5的Newmark法，该方法的主要缺点是无法滤掉虚假的高阶分量。

动力学切线刚度矩阵(即迭代中的雅可比矩阵)为

(12)

(13)

(14)

(15)

(16)

此处略去切线刚度矩阵繁琐的推导过程。由此在t+Δt时刻的Newton-Raphson迭代格式为

(17)

需要注意的是，HHT法在单元过程中要单独计算上一时刻应力的节点等效力，且外载荷是t+(1+α)Δt时刻的。

4 铰接和刚性连接的处理

ANCF大柔度梁/绳索单元使用切线的斜率为自由度，在刚性连接中，连接处的节点具有不同的切线方向，因此应作特别处理。

如图2所示，节点i和节点j分别铰接或刚性连接，约束方程为

(18)

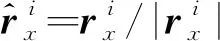
图2 铰链和刚性连接

(19)

(20)

式中0为3×1的零矢量或3×3的零矩阵，C1和C2是罚因子，即相应的弹簧刚度。本文算例表明，可分别取为拉伸和弯曲切线刚度矩阵最大元素的1000倍。切线刚度矩阵第三项的推导中考虑矢量模的倒数为常数，从而简化计算过程。

5 数值算例

5.1 弦的微幅和小幅振动

弦在张紧状态下作横向微幅振动时，内部张力可视为常数。图3所示的弦，长为1 m，直径为0.2 mm，弹性模量为200 GPa，密度为7800 kg/m3，两端简支，弦的张力T=5 N。初始时受外部约束而水平静置，突然撤去外部约束后，弦在重力作用下发生微幅振动，其理论解为

(21)

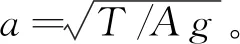
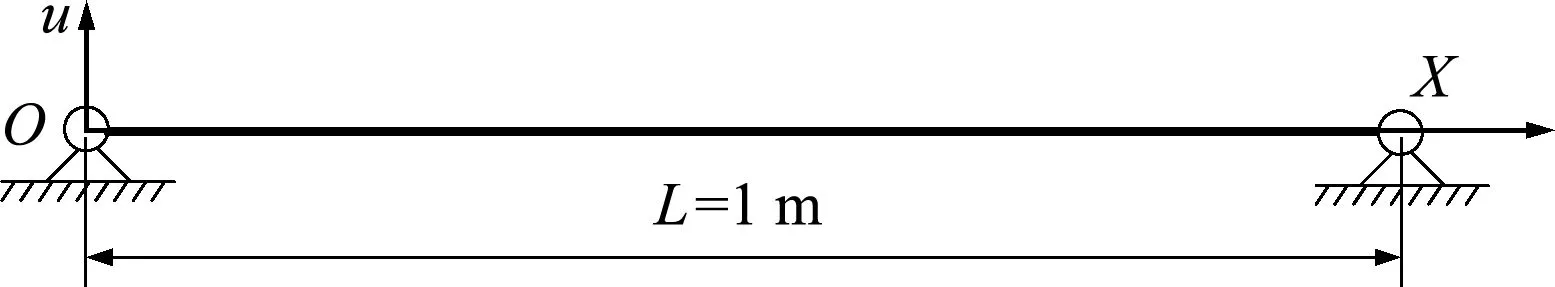
图3 振动的弦

使用20个ANCF绳索单元模拟，HHT中积分参数α取为-0.005，时间步长取为10-4s。图4是弦中点横向位移的理论解(21)与ANCF数值解的对比(每30个时间步输出一个结果)。弦中点的最大振幅为0.1201 mm，符合微幅振动的假设。模拟结果与理论解符合得很好。

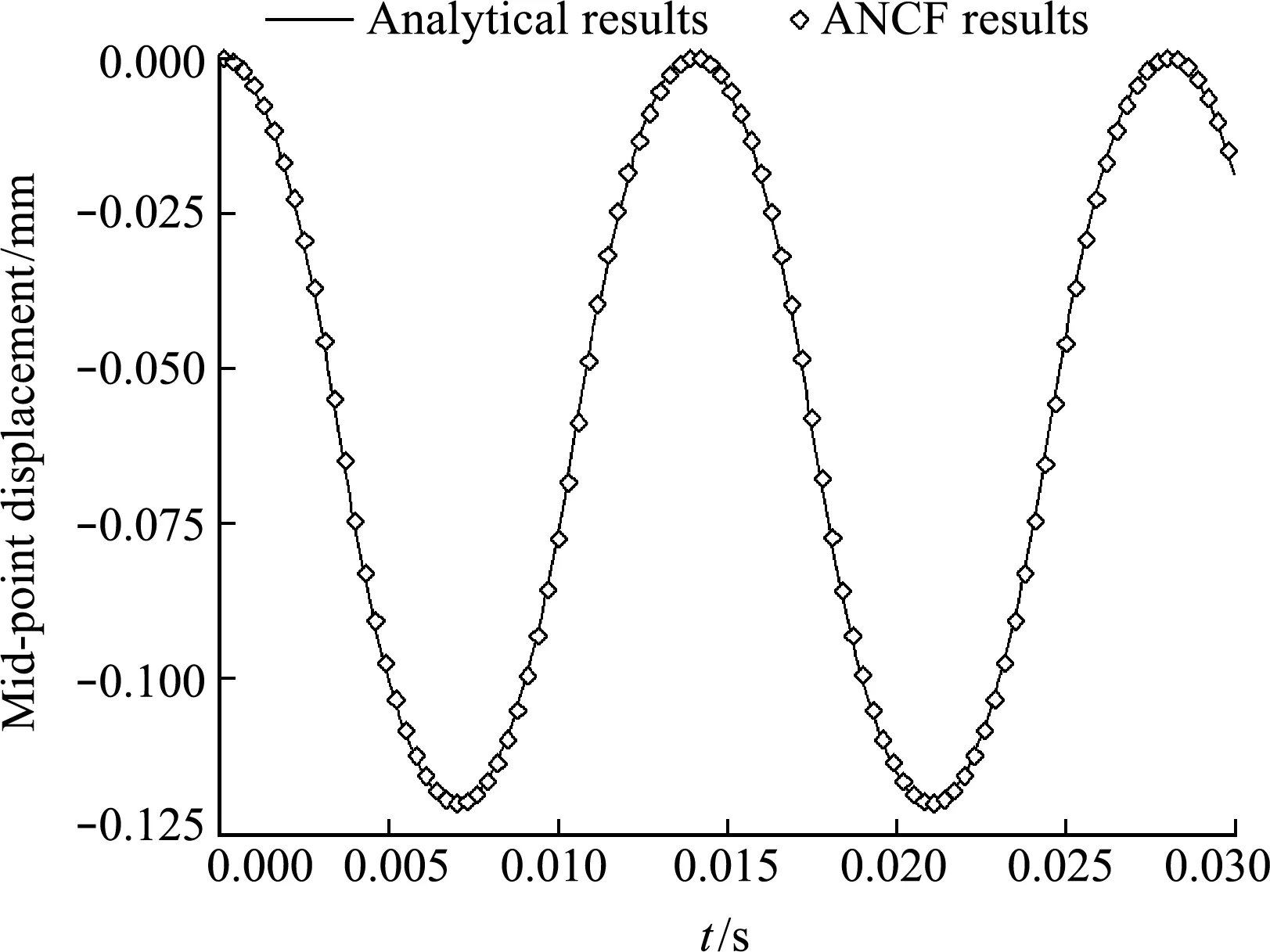
图4 中点位移的对比

进一步考察在弦中点受冲击载荷作用下的响应，载荷为0 s ～0.02 s内一幅值Q为1 N或10 N的三角形力波。由于未有该情况下的解析解，故将ANCF的数值解与ANSYS中采用三次插值模式的Beam188单元的结果进行对比。将弦均分为20个单元，ANCF采用α为-0.005得HHT格式，时间步长为10-4s；ANSYS采用Newmark格式，时间步长为10-5s。

图5列出了在冲击载荷幅值分别是1 N和 10 N 时，弦中点的位移时程，此时最大振幅分别超过了30 mm和65 mm，已不再符合微幅振动假设。ANCF数值结果与ANSYS结果符合得较好。

5.2 双杆摆和T字形杆摆

为考察本文算法对于大刚度梁的模拟和约束处理，模拟图6的直径为2 cm的圆截面钢梁，弹性模量为200 GPa，密度为7800 kg/m3，其中图6(a)为两根长为0.5 m的杆铰接而形成的双摆； 图6(b)为T字形摆，各段长度均为0.5 m。均由水平位置无初速度释放，各段等分为两个单元，采用α为-0.005的HHT方法，时间步长均为10-3s。

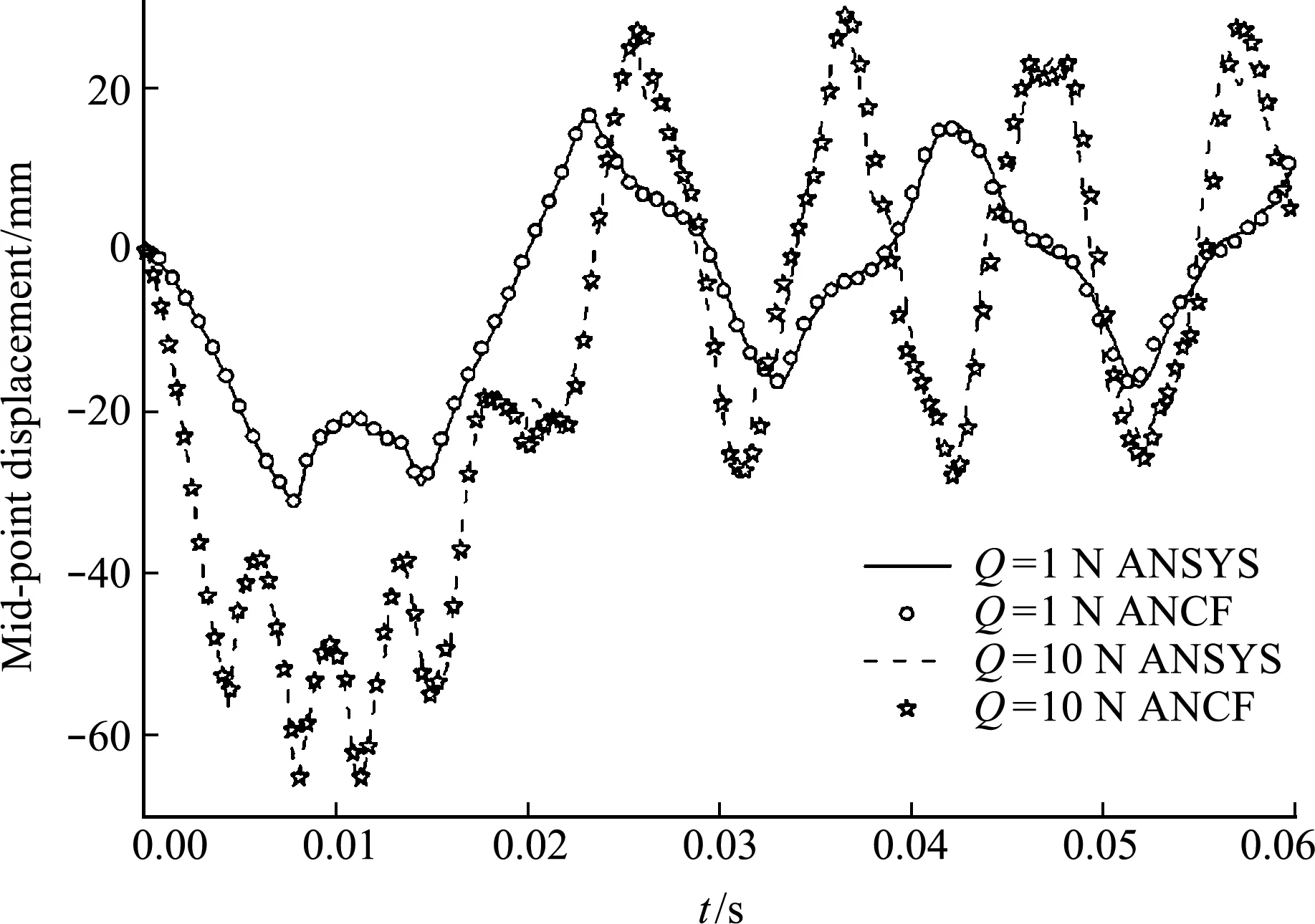
图5 冲击载荷下中点位移的对比

图7为铰接的两个节点距离的时间历程，距离越小表明约束效果越好，图7列出了不同罚因子C1水平的模拟结果。罚因子0.01EA/L(L=1 m)时，铰接节点的最大距离为94.07 μm，约束效果好。增大罚因子能达到更好的约束效果，但罚因子增大到1013EA/L会导致不收敛。

T字摆的模拟中，C1设置为103EA/L(L=1 m)，C2参照抗弯刚度EI/L进行设置。图8为节点切线夹角θ0与直角之差的时间历程。罚因子0.1EI/L能达到较好的约束效果，θ0与直角相差不超过1.5°，进一步增大罚因子至EI/L，θ0与直角相差不超过0.2°，但增大至100EI/L不收敛。

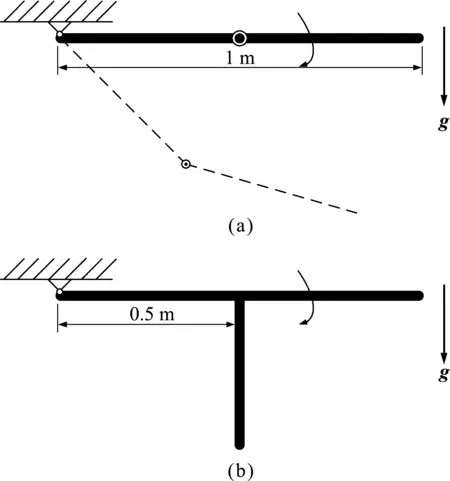
图6 双杆摆和T字形摆

图7 铰接节点距离的时间历程

5.3 自由下落的柔绳

计算一根水平放置、左端铰接于地面的柔绳，无初速度释放，在重力作用下自由下落。绳长为 1.2 m，圆截面面积为0.0018 m2，截面惯性矩为 1.215×10-8m4，密度为5540 kg/m3，弹性模量为 0.7 MPa。

将模拟结果与已有结果[18]进行比较。节点等效力分别为小变形的Model I[19]、小/大变形的Model V[18]、符号运算的Model S以及本文的公式(6～8)。此前的算例采用四阶龙格-库塔法的显式格式，本文算例采用HHT法的隐式格式，时间步长设置为10-3s。

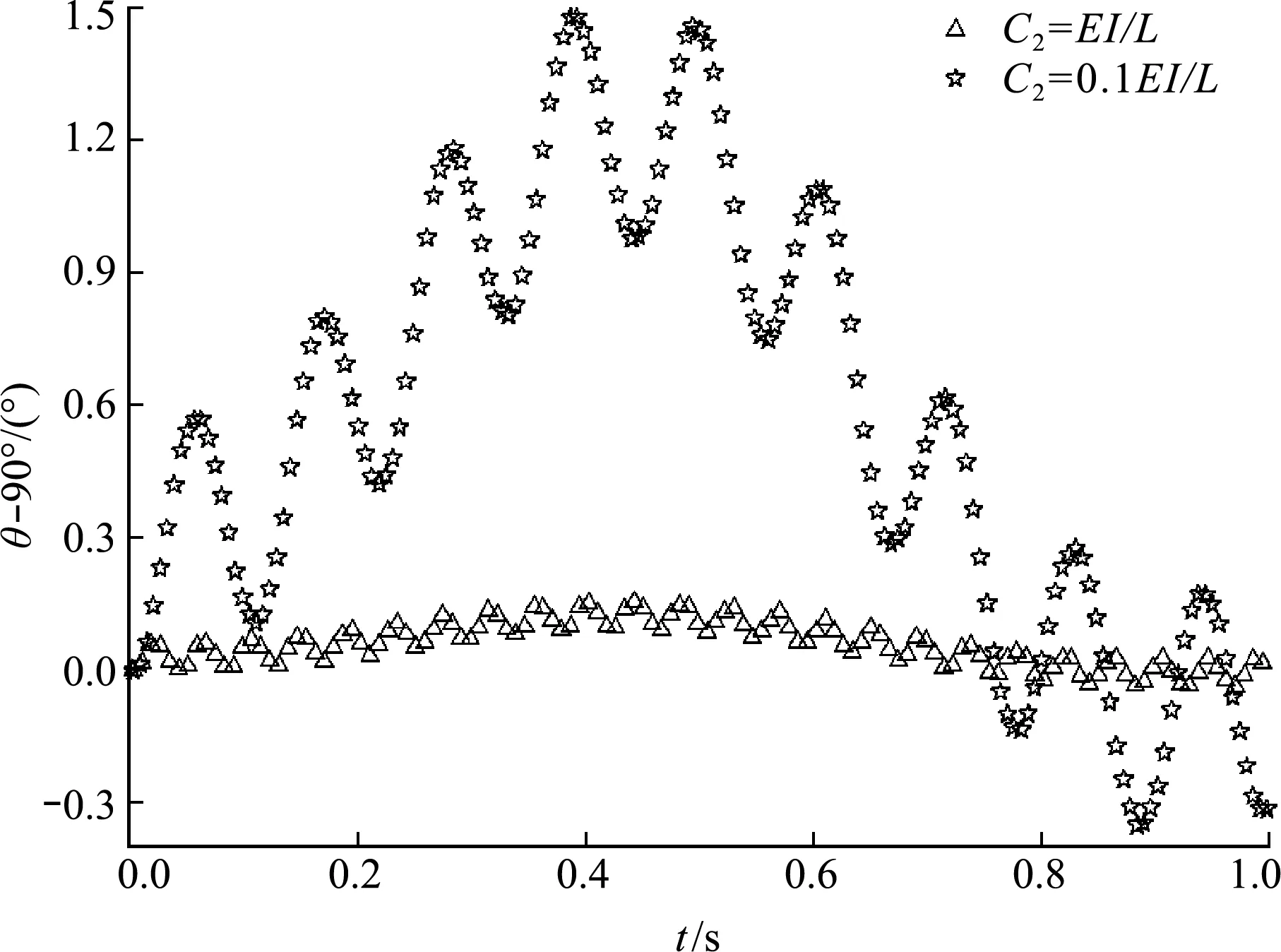
图8 θ0和90°的对比

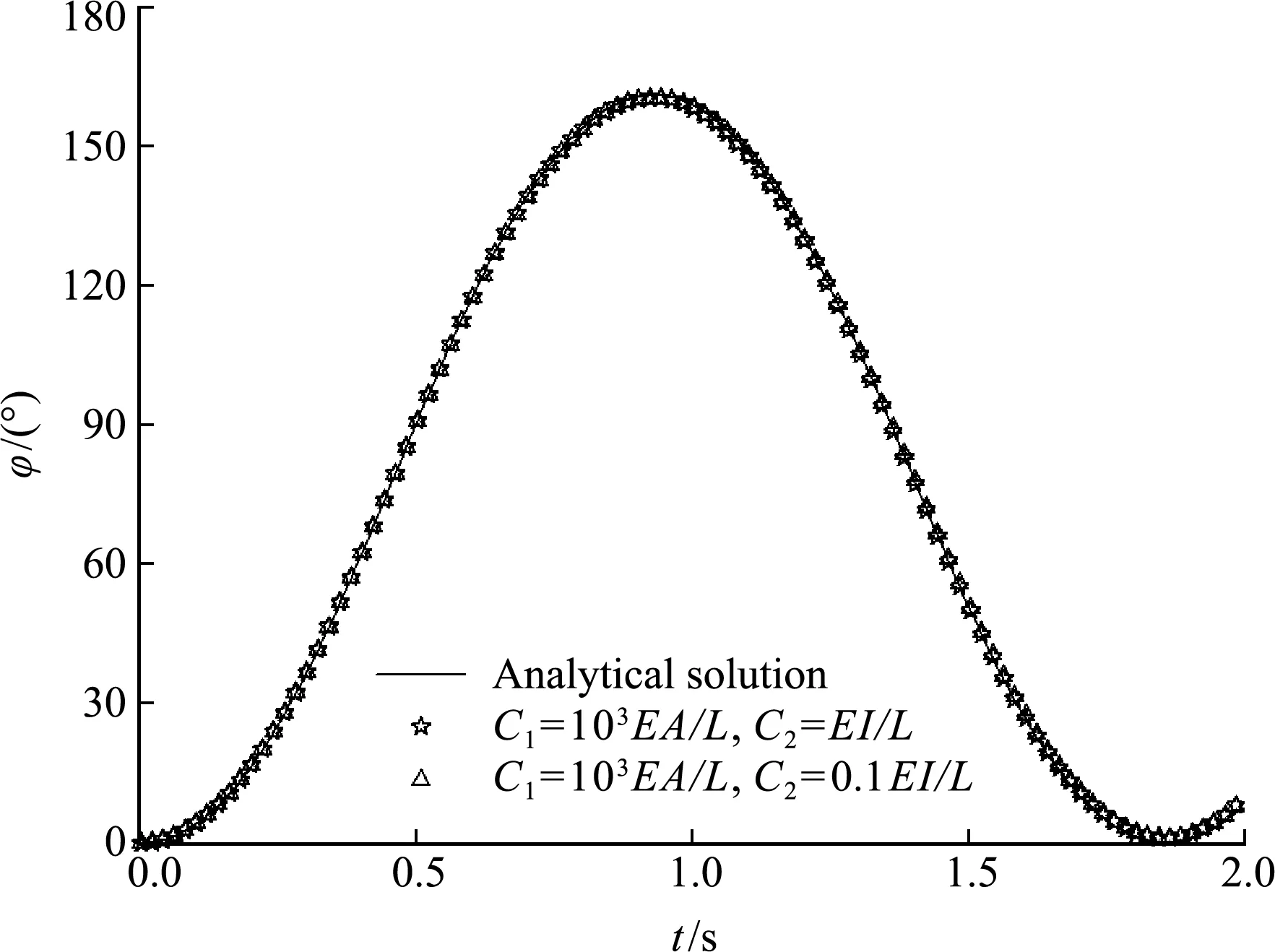
图9 T字形杆摆动的ANCF结果和解析解

图10是自由端铅垂位置的时程曲线。本文算法的模拟结果与已有结果符合得较好，证明了本文公式及隐式迭代格式的正确性。考虑绳索水平释放，在0.7 s时解除约束的情况，图11为柔绳各时刻的形状。

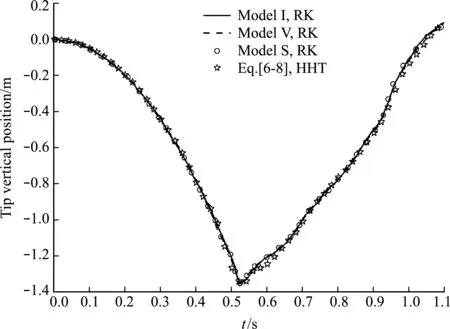
图10 自由端的铅垂位置

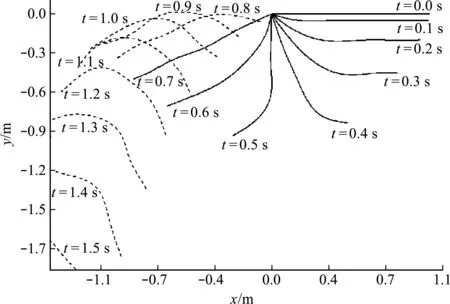
图11 绳索各时刻的形状

6 结 论

(1) 为有效模拟大柔度梁/绳索结构的大范围运动和变形，针对ANCF大柔度梁/绳索单元建立了基于HHT方法的绳索隐式动力学迭代格式。

(2) 将矢量叉乘改写为矩阵相乘，得到了 ANCF 大柔度梁/绳索单元的节点等效力公式，进一步由节点等效力导出了切线刚度矩阵的全部公式。

(3) 本文算法的模拟结果与理论解及已有结果符合得较好，验证了节点等效力公式、切线刚度矩阵公式、及所建立的隐迭代格式的正确性。

(4) 采用罚方法处理ANCF的约束方程，实现了梁/绳索间的铰接和刚性连接。数值模拟结果表明罚方法能够有效实施此两种约束。