小学生的思维能力培养路径探寻

葛瑶

[摘  要] 没有思维，就没有真正的数学学习。小学数学教学中，教师可从对话、操作、融错、等待中培养学生的数学思维，追求数学的思维之美。

[关键词] 数学思维;路径;对话;操作;融错;等待

没有思维，就没有真正的数学学习。知识是思维的载体，思维是获得知识的重要途径。在数学课堂教学中，教师应把培养数学思维贯穿于教学的各个环节，追求数学的思维之美。

一、对话，在语言中体现数学的思维之美

数学教学在对话之中实现交流互动，课堂教学模式由“教师独白”走向“师生对话”，最终把数学课堂塑造成“师生对话的共同体”。在数学课堂教学中，教师应不断丰富对话内容，改进对话方式，激发学生表达内心想法的动机，在师生之间的对话与互动中培养学生的数学思维[1]。

案例1  “平行四边形面积”教学节选

师：在实际生活中，我们经常会遇到平行四边形，比如一些花坛为了美观，往往设计成平行四边形的形状，那么，我们应该如何来求平行四边形的面积呢？

生1：可以用数格子的方法。

生2：数格子的方法太麻烦了，而且也不准确。

师：好的，那我们先来试一试数格子的方法（如图1）。

生3：平行四边形一共占了24个格子。

师：这个平行四边形的确占了24个格子，但是我们也发现数格子这个方法很慢，而且容易出差错。那么，有没有更好的办法呢？

（学生思考。）

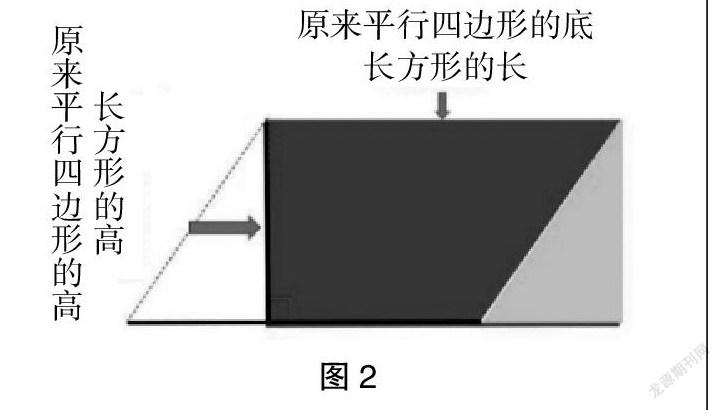
师：我们已经学过了如何求长方形的面积，能不能把平行四边形转化成长方形呢？我们来看下面的图形（如图2）。

生1：这是割补法。

生2：白色三角形的面积与黄色三角形的面积相等。

生3：这样平行四边形的面积就转化成了长方形的面积。

师：我们来分析一下平行四边形的面积是怎么算的。谁知道长方形的面积是怎么计算的？

生：长方形的面积=长×宽。

师：在这里，长方形的长相当于什么？长方形的宽又相当于什么？

生：长方形的长就是原来平行四边形的底，而长方形的宽就是原来平行四边形的高。

师：那么，我们可以得出公式“平行四边形的面积=底×高”。

对话，实际上是学生思维的外在表现形式。教学中，教师提出问题，激发学生思考，学生结合已学知识采用“数格子法”来解决问题，在学生得出基本结论时，教师趁势进行启发：“能不能把平行四邊形的面积转化为长方形的面积？”寥寥数语，提醒学生要对自身的思维方式进行反思和调整，正是这种步步引导的提问与对话，激发了学生的辩论与思考，让学生在思维火花的碰撞过程中深化了数学思维。

二、操作，在行动中体现数学的思维之美

操作，在学生的数学学习中具有重要的作用。在教学中，教师应为学生的实践操作提供机会和平台，使学生在提出问题、实践操作、探索结论和评价反思中获得数学知识，发展数学思维[2]。

案例2  “圆的面积”教学节选

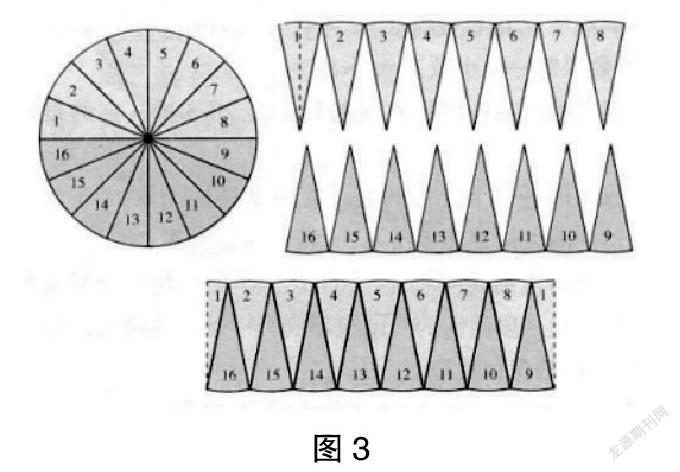
师：我们来看一道题。温馨家园小区的一个井盖的半径是50cm，那么我们应该怎样求这个井盖的面积呢？我们先看下面这个图，同学们都非常喜欢剪纸吧，现在就让我们拿出一张白纸，剪一个半径为5厘米的圆，沿着这个圆的直径把圆剪切成两个半圆，然后分别涂上不同的颜色，再剪成16个大小相同的小扇形（写上标号），最后将得到的图形拼接起来。（如图3）

（学生操作。）

生1：这是我的作品。（展示）我发现通过裁剪把一个圆变成了类似于平行四边形的图形。

生2：我也完成了。我发现圆的面积和这个平行四边形的面积是相等的。

师：刚才这位同学说圆的面积与平行四边形的面积相等，谁能说说理由？

生3：因为我们用的纸并没有变多，也没有变少，只是换了一个样子而已。

师：好的。那么，这个平行四边形的底和高与圆之间存在怎样的联系呢？

（学生思考。）

生1：平行四边形的高就是圆的半径。

生2：平行四边形的底是圆周长的一半。

师：非常好。现在，我们就可以得出圆的面积公式S=×r=（πr）×r=πr2。

师：现在我们回到课堂刚开始提出的问题，温馨家园小区的一个井盖的半径是50cm，我们应该怎样求这个井盖的面积？

生3：已知圆的半径，可以直接求出圆的面积。

生1：S=πr2=3.14×502=3.14×2500=

7850（cm2）。

师：同学们，通过今天的学习，我们学会了通过操作进行转化，这在数学的学习过程中是非常重要的。

教学中，教师结合学生的认知特点，给予学生充分的自主权，使学生通过画一画、剪一剪、想一想、算一算，亲历圆面积公式的来龙去脉，最终完成新知识的同化和建构，促进了学生思维的发展。

三、融错，在思辨中体现数学的思维之美

学习的过程是一个循序渐进、不断试误的过程，教师要正确看待学生在学习中的差错，允许和尊重学生在合理范围内出现的错误，以一颗包容之心使学生放下羁绊，在课堂上积极思考、自由翱翔[3]。

案例3  “正方体的体积”教学节选

师：有这样一道题，如果一个正方体的棱长是6厘米，那么，它的体积和表面积相等。请问这句话对吗？

（题目一出，学生马上就分成了两大阵营，有的说对，有的大声否定。）

师：看来同学们在这道题上产生了不小的分歧，现在我们不妨各抒己见，展开辩论，看看这道题的结果到底如何。

生1：我认为这句话是对的。因为正方体的表面积S=6a2，正方体的体积V=a3，我们把6代入公式，很容易就能得出它们的结果都是216，所以这句话是正确的。

生2：我认为这句话不对。

师：现在我们请生2来说说自己的看法。

生2（迫不及待）：生1提供的公式是没有问题的，尽管按照生1的公式的确得出了216，但是表面积和体积的单位是不一樣的，表面积单位和体积单位没有可比性。

师：很好。生2的分析非常透彻。没有可比性的两个量无法比较大小，就好像5千克和5厘米无法比较大小是一样的道理。

融错是一种包容，融错更是一种智慧。教学中，教师通过使“两大阵营”的学生自由发表意见，让学生在两种思想的不断摩擦和碰撞中得出真理，从而加深了学生对数学规律性的深刻理解。

四、等待，在静默中体现数学的思维之美

学习的过程是主动探究的过程，也是对知识建构的过程，而无论是探究还是建构，都需要一个过程。“教育是慢的艺术。”在教学中，教师要学会耐心等待，给予学生足够的时间和空间对知识进行探究和建构，进而完成对知识的吸收和内化[4]。

案例4  在讲述游戏规则的公平性的相关知识后，教师出示了这样一道题：淘气和笑笑玩掷骰子游戏，他们约定如果掷到质数，淘气赢;如果掷到合数，笑笑赢;如果掷到既不是质数也不是合数，双方不输不赢。同学们认为这个游戏规则公平吗？

（学生思考约两分钟。）

生1：我认为这个游戏规则不公平。在1～6中，质数有：2、3、5，合数有4、6，1既不是质数也不是合数。因此，淘气赢得机会更大些。

师：生1的回答非常准确，能够把学到的理论知识应用到实际生活中去。现在我们再大胆地挑战一下自己，这个游戏规则应怎样制定才能更加公平？谁来说一下。

生2：掷到奇数是淘气赢，掷到偶数是笑笑赢，这样就公平了。

师：生2的回答非常好。还有其他答案吗？

（学生思考，教师等待。）

生3：掷到1、2、3是淘气赢，掷到4、5、6是笑笑赢，这样也是公平的。

师：同学们考虑到了各种情况，这一点很好。还有其他答案吗？

（学生思考，教师等待。）

生1：任意选择3个不同的数字淘气赢，剩下的3个数字笑笑赢，这种方式也是公平的。

师：非常好，这位同学的回答抓住了这道题的本质，这说明他对游戏规则的公平性的认识是深刻的。

学生的凝神静思源于教师的耐心等待。教学中，教师在每一次提问之后都会给予学生思考的时间，也正是通过一个个提问、思考、等待、指导的环节才使得数学课更加包容、更加思辨、更加精彩。

总之，数学的学习是一个动态的过程，教师要以“书是音符，谈话才是歌”的态度鼓励学生对话交流，以“纸上得来终觉浅”的精神鼓励学生动手操作，以“过尽千帆皆不是”的严谨鼓励学生大胆试误，以“时光不语，静待花开”的耐心等待学生成长。唯有如此，数学课堂才能绽放出思维之美，更加精彩。

参考文献：

[1]  乔登娥. 小学数学课堂教学语言案例分析[J]. 教育革新，2020（08）.

[2]  李志川. 优化小学数学动手操作  促进学习真正发生[J]. 福建教育学院学报，2019，20（06）.

[3]  杨海燕. 锤炼等待艺术，打造小学数学高效课堂[J]. 陕西教育（教学版），2018（12）.

[4]  杨小秋，陈嘉雯. 从“试”到“悟”的小学数学教学“融错”策略的应用[J]. 现代中小学教育，2017，33（11）.