基于故障观测器的多无人机姿态一致性控制

唐 余，薛智爽，刘小芳，刘永春，张 果，余 亮

（1.四川轻化工大学人工智能四川省重点实验室，四川自贡 643000；2.四川轻化工大学自动化与信息工程学院，四川自贡 643000；3.四川轻化工大学计算机科学与工程学院，四川自贡 643000；4.四川轻化工大学物理与电子信息工程学院，四川自贡 643000）

0 概述

多无人机协同控制技术是利用多架无人机通过任务分配及调度的方式完成指定任务，近年来在军事、民用等领域具有广泛的应用。在多数情况下，使用多个无人机协同工作比使用单个无人机更为有效，比如在大范围内搜索目标以及绘制地图时，可通过无人机团队合作实现空中加油的任务［1-3］。多无人机协同控制中最基本的问题是一致性问题，是指在一个集群中的无人机基于相邻无人机信息以及一致性控制协议同步到一个公共状态中［4-5］，这种一致性控制协议可分为非主从式控制协议和主从式控制协议［6-7］两类。主从式一致性控制是所有无人机都相对领导者或参考信号进行同步。由于无人机进行长时高空作业时，不仅需要应对来自外部的干扰，还需要解决由于机体内部的零件磨损和退化引起的模型或参数不确定、测量存在误差以及控制器微小故障等问题。在实际应用过程中，无人机真实模型的获取较为困难，而仅基于无人机名义模型设计的一致性控制器不能使得无人机按照期望的姿态飞行。

文献［8］针对四旋翼无人机姿态控制问题，提出一种基于干扰观测器的轨迹跟踪鲁棒控制算法。通过对未知气动干扰力矩进行观测，并在控制输入中加入干扰力矩的观测值，确保姿态子系统能够以指数收敛速率跟踪中间指令信号。文献［9］提出一种基于多输入多输出扩展状态观测器的新型水下机器人积分滑模控制器，并利用自适应增益更新算法估计不确定性的上界，实现水下机器人对期望姿态的渐近跟踪。文献［10］针对具有未知扰动的非线性多智能体系统的事件触发跟踪控制问题，通过设计扰动观测器来估计未知的外部扰动，并基于Lyapunov稳定性理论和Backstepping 方法，证明一致性跟踪误差位于原点的一个小邻域内。文献［11］在模型或参数不确定、未知海洋扰动和伴随测量误差的情况下，关于有向网络上由多个动态领导者引导的网络化自主水下机器人的围堵控制问题，提出一种新的基于预测器的神经动态曲面控制设计方法。该方法可用于开发自适应包容控制器，使机器人的运动轨迹收敛于领导者附近。文献［12］在设计的控制器中直接构造神经网络，以解决干扰及模型不确定等问题造成的不利影响，并实现多无人机姿态的一致性控制。然而，上述姿态控制方法仅考虑了姿态跟踪中的单个干扰问题，并未综合考虑姿态跟踪中出现的复合干扰问题，因此姿态的同步性能还有待提高。

本文基于观测器理论［13-14］提出一种故障检测方法，对外部干扰、模型不确定、测量误差以及控制器微小故障等问题进行实时估计，并结合无人机名义模型设计一致性控制器，解决由于上述故障与干扰引起的飞行姿态不理想问题，通过与文献［12］所提控制器进行对比，以验证该控制器的有效性。

1 无人机姿态系统的数学模型

为了方便起见，本文使用的符号表示如下含义：

1）ℝ 表示常数空间，ℝn表示n维向量空间，ℝn×m表示n×m维的矩阵空间，In表示n×n维的单位矩阵。

2）tr(·)表示求解矩阵的迹，·T表示矩阵转置，·+表示求解矩阵的Moore-Penrose 广义逆，diag(·) 表示构造对角矩阵，λmin(·)和λmax(·)分别为矩阵的最小和最大特征值。

3）⊗表示求解克罗内克积。

固定翼无人机姿态在空间中的运动具有3 个绕质心旋转的自由度，分别为滚转、俯仰和偏航运动。无人机的副翼和升降翼相互作用产生滚转力矩和俯仰力矩，而方向翼产生偏航力矩。如图1 所示，无人机的运动涉及惯性坐标系、机体坐标系和气流坐标系，并分别用字母n、b和w表示。

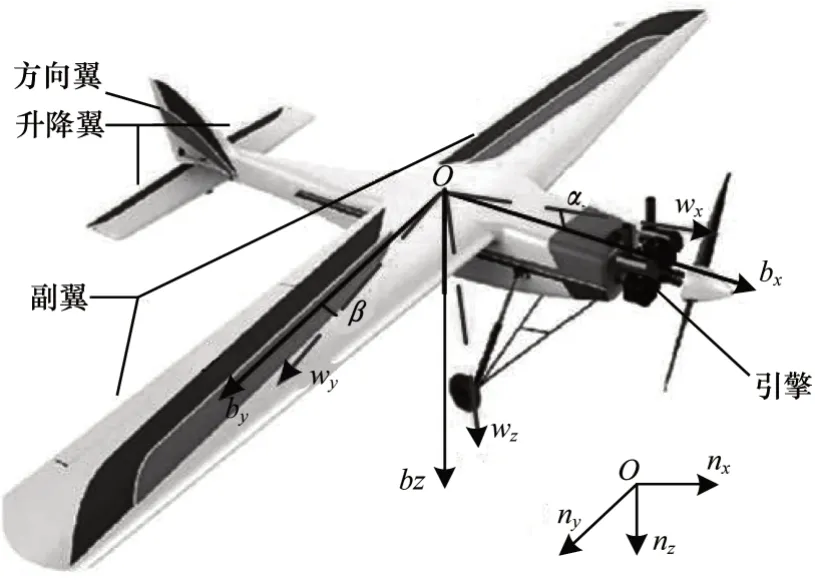
图1 固定翼无人机模型及其惯性坐标系Fig.1 Fixed wing UAV model and its inertial coordinate system

以无人机i为例，其相对于惯性坐标系的滚转、俯仰和偏航姿态角分别用欧拉角φi、θi和ψi表示，相对于机体坐标系的姿态角速度分别用pi、qi和ri表示。其中，i∈[1，2，…，N]，N为实现姿态同步的无人机数量。令，则两者之间具有如下转换关系：

根据牛顿力学［15］可推导出无人机i姿态系统的动力学方程为：

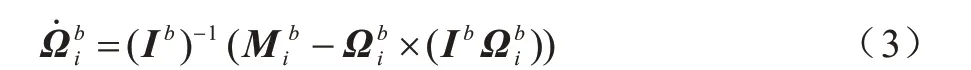
其中，Ib是通用无人机转动惯量矩阵，其完整形式如式（4）所示。

式（8）为无人机姿态系统名义模型（无模型不确定及外部干扰下无人机姿态系统的数学模型）的状态空间方程。Ai∈ℝ3×3、Bi∈ℝ3×5和Qi∈ℝ3为名义模型，它们的完整形式如下所示：

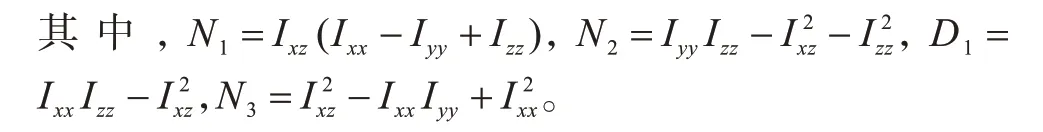
2 基于观测器的故障检测方法

结合式（8），在干扰、模型不确定、状态测量误差以及控制器微小故障下，一类非线性多无人机姿态运动数学模型可以建模为以下微分方程：

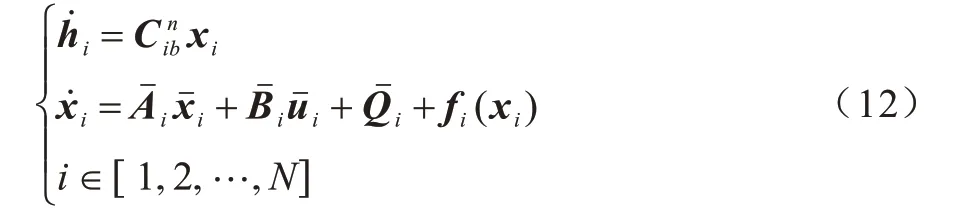
理论上式（12）可以等价为：

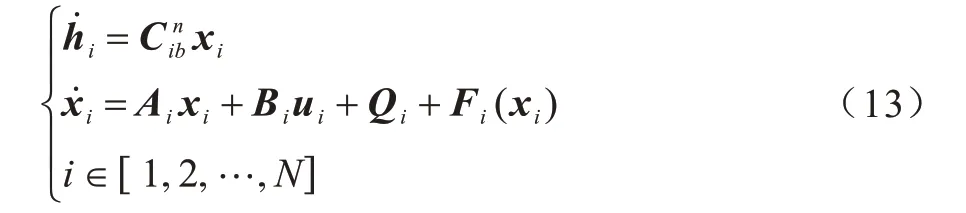
其中，Fi(t)为包含干扰、模型不确定、状态测量误差以及控制器微小故障的集成不确定项，其具体形式为：

为方便使用观测器观测集成不确定项，可截取式（13）中包含集成不确定项的部分，并在此基础上设计如下包含输出方程的多无人机姿态运动方程：

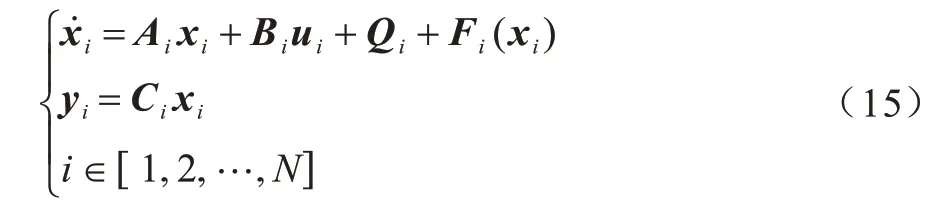
其中，yi(t)为输出向量，Ci=Im为输出矩阵，Im为维数为m的单位矩阵，m为状态向量的维数。

式（15）对应的模型不确定及干扰观测器可被定义为：

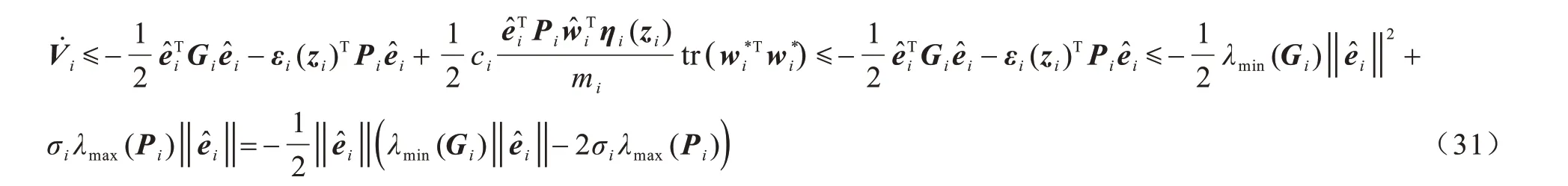
因此，可得出以下结论：Lyapunov 函数Vi将收敛到半径附近，κi=2λmax(Pi)/λmin(Qi)，其中σi为足够小的正常数，κi的值可以通过调整参数Pi和Qi而设计到足够小，理论上构造函数Vi的观测误差和神经网络权值估计误差将收敛到足够小。

3 主从式多无人机姿态一致性控制

因为式（13）与式（15）等价，所以适用于式（15）的控制器同样适用于式（13），本文将在式（15）的基础上设计出多无人机姿态一致性控制器，且在设计主从式多无人机姿态一致性控制器过程中，须给出参考信号或领导者状态方程：

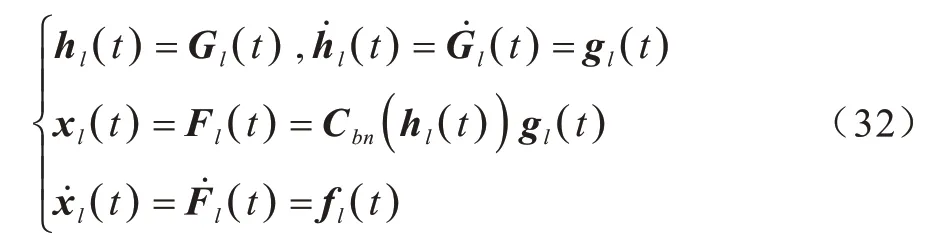
其中，hl(t)，xl∈ℝ3为领导者状态，fl(t)∈ℝ3为有界光滑向量函数且‖fl(t) ‖＜ε。本文控制任务是在模型不确定、外部干扰以及智能体与领导者之间通信受限（只有部分无人机能与领导者通信）下，设计一致性控制方案，使得每个无人机xi都能精确跟踪领导者状态hl(t)和xl，即limt→∞(‖xi(t)-xl(t) ‖+‖hi(t)-hl(t)‖)=0。

为实现无人机姿态的一致性，本文引用了图论［17-18］，一个无向图可定义为：

其中，v=[v1，v2，…，vN]为图节点集，ε⊆v×v为图边集。

根据文献［17-18］可知，如果在2 个节点之间存在一条边，则表示这2 个节点互为邻接节点。如果图Γ中任意2 个节点之间存在路径，则称该图为连通图。结合式（33），将N个需实现姿态同步的无人机视作v中的节点，则该无人机之间的关系可以用图Γ表示。图Γ的邻接权重矩阵可以表示为：

其中，aii=0 且aik=aki，如果无人机i和无人机k之间存在通信，则aik＞0，且矩阵A的Laplace 矩阵L为：

其中，D=diag(d1，d2，…，dN)∈ℝN×N，

结合式（12）和式（32），则无人机i和领导者之间的跟踪误差可定义为：

根据文献［19］可知，无人机i的主从式一致性误差可定义为：

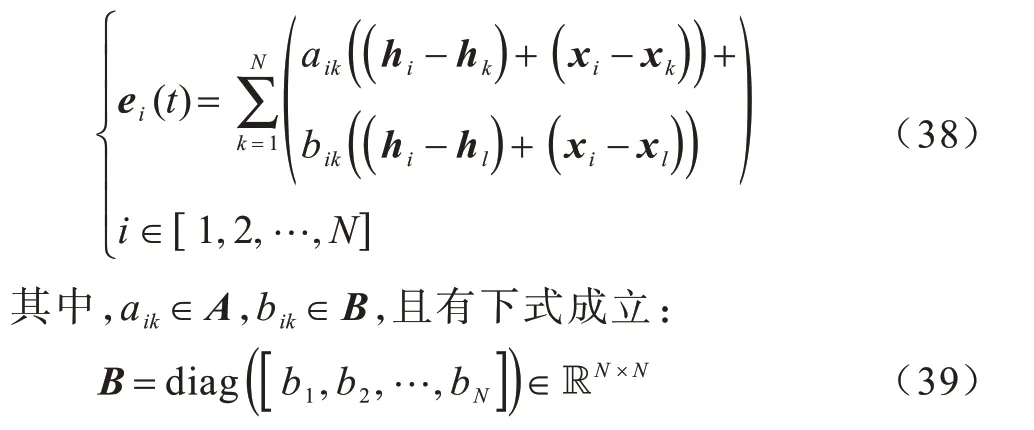
式（39）为无人机与领导者之间的通信权重矩阵，当且仅当bi＞0 时，无人机i和领导者之间存在信息交换。结合式（36），则式（38）可重新表示为：

对于Laplace 矩阵L而言，其特征值为非负，因此矩阵=L+B特征值也为非负。因此，定义一个Lyapunov 正定函数为：

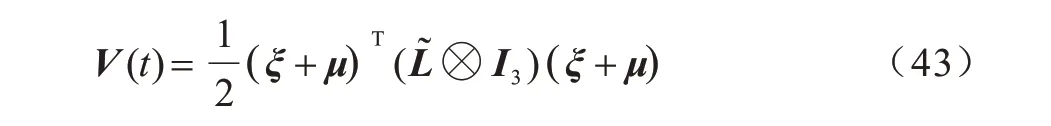
其中，正定矩阵⊗I3∈ℝ3N×3N可以被分解为如式（44）所示。

其中，M∈ℝ3N×3N和Λ∈ℝ3N×3N分别为⊗I3的特征向量矩阵和特征值矩阵，且MT=M-1。

结合式（44），Lyapunov 函数V(t)可被重写为：

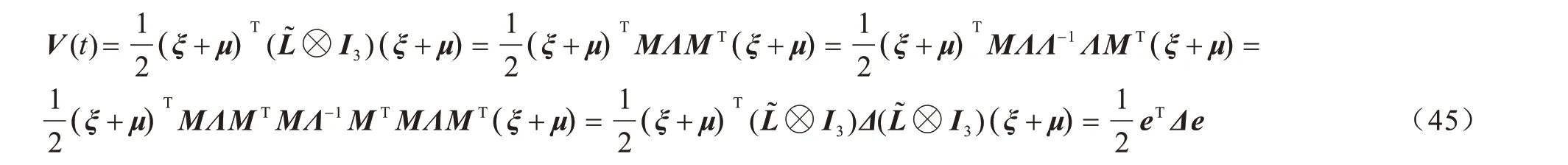
结合式（16）～式（31）中基于观测器与神经网络设计的集成不确定项估计器(xi)，伴随集成不确定项时的多无人机姿态一致性同步控制器可设计为：

式（56）表明，包含集成不确定项估计误差的参数ρˉ能够收敛到足够小，且通过选择合适的参数，Lyapunov 函数V(t)也能收敛到足够小，进而确保一致性误差收敛到足够小。

4 仿真与结果分析

为了验证本文提出的针对无人机模型不确定及外部干扰下的主从式多无人机姿态一致性控制方案的有效性，实验运用MATLAB R2016b 环境进行仿真与分析。实验选择6 架飞机进行模型不确定及外部干扰下的姿态一致性仿真，构建无人机模型所需参数见表1。

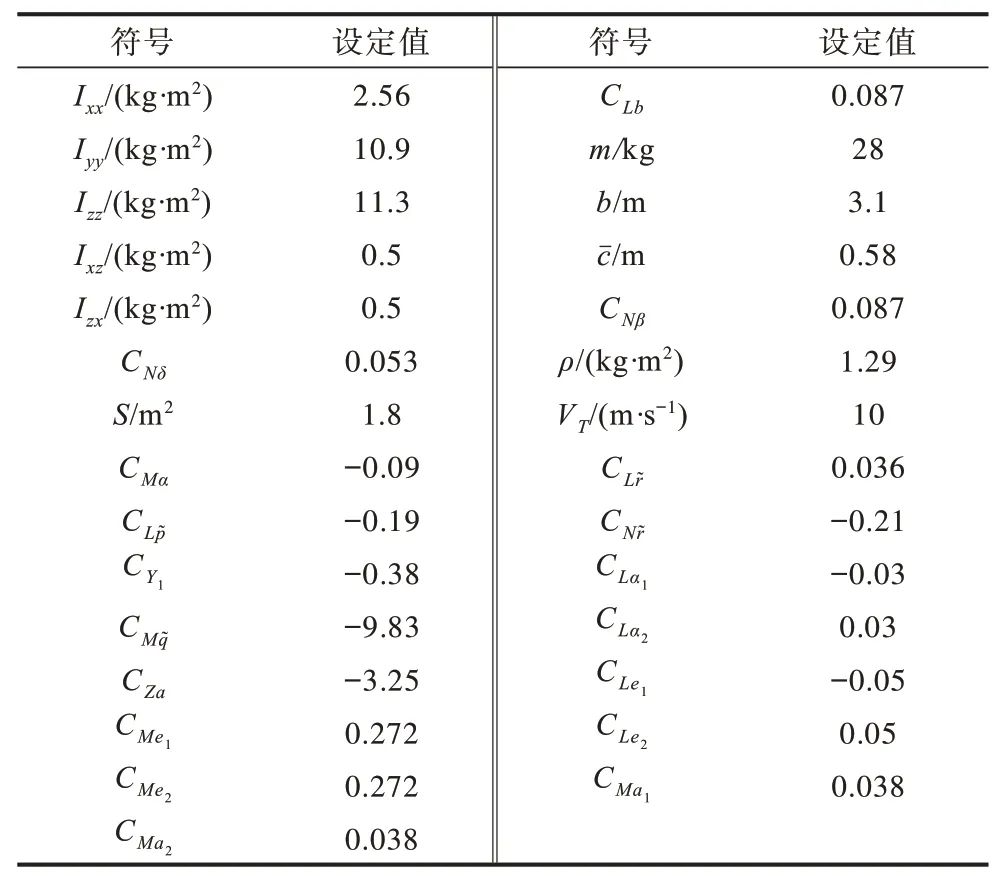
表1 无人机姿态运动模型的相关参数设置Table 1 Parameter setting of UAV attitude motion model

本文给出：

式（57）为领导者与无人机之间的通信权重矩阵，表明只有无人机1 和无人机5 与领导者之间存在信息交换，且无人机之间的邻接权重矩阵为：

式（58）表明无人机之间存在通信。

给出惯性坐标系下的领导者姿态为：

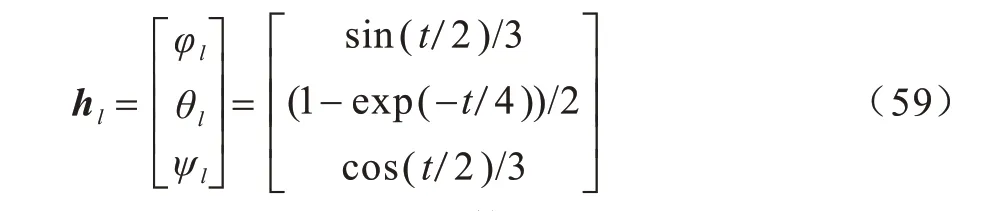
由式（59）可得出在机体坐标系下的领导者姿态角速度函数为：

各无人机的初始姿态取值为弧度-1 到1 之间的随机数。各无人机所受外部干扰、模型不确定项、状态测量误差及控制器微小故障为：

此外，为了对比验证本文提出的故障检测方案的性能，根据文献［12］设置区别式（50）的控制器（基于神经网络的直接自适应控制器）为：

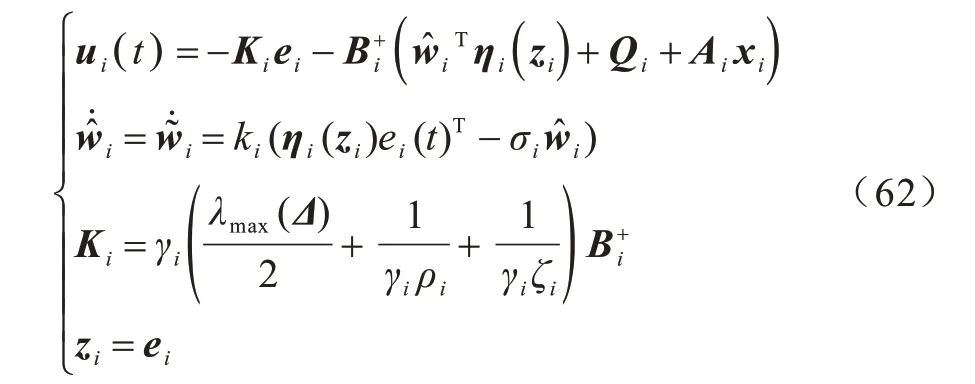
本文提出方法以及对比方法的控制参数相同，具体如表2 所示。

表2 各无人机所需控制参数Table 2 Control parameters of each UAV

本文提出的基于观测器的间接自适应一致性方法的仿真结果如图2 和图3 所示。图2 给出了无人机1 在惯性坐标系下相对于领导者姿态跟踪的效果，图3 给出了无人机1 主从式一致性误差随时间的变化情况。

图2 式（50）控制下无人机相对于领导者的姿态同步效果Fig.2 Attitude synchronization effect of UAV relative to leader under the control of Eq.（50）

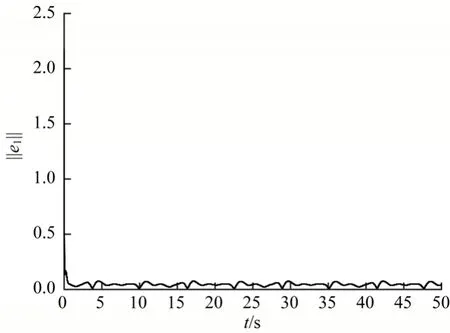
图3 式（50）控制下无人机主从式一致性误差Fig.3 Leader-follower consistency error of UAV under the control of Eq.（50）

无人机1 和无人机2 的集成不确定项及估计值随时间的变化情况如图4 所示。从中可以看出曲线的拟合度较好，这说明本文设计的控制器能够补偿不确定项给无人机同步带来的干扰。图5给出了无人机不确定项估计误差随时间的变化情况。基于文献［12］提出的神经网络直接自适应一致性方法的仿真结果如图6～图9 所示。图6 给出了无人机1 在惯性坐标系下相对于领导者姿态跟踪的效果，图7 给出了无人机1 主从式一致性误差随时间的变化情况，图8 给出了无人机不确定项估计误差随时间的变化情况，图9 给出了无人机1 和无人机2 的集成不确定项及估计值随时间的变化情况。从图2、图3 与图6、图7 的姿态一致性跟踪效果可以看出，基于神经网络的直接姿态一致性控制方法的控制效果明显较差，相比基于观测器的间接姿态一致性控制方法，姿态在同步过程中有明显波动且无人机的主从式一致性误差也较大。通过对比图4、图5 与图8、图9 可知，基于观测器的间接不确定项估计方法对初期无人机不确定项的估计过程虽然有一定的抖动，但是相比基于神经网络设计的直接不确定项估计方法，最终稳定的不确定项估计误差波动范围较小，对不确定项的估计更为精确且快速。

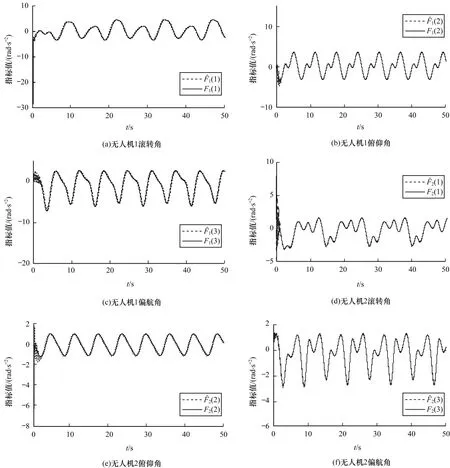
图4 式（50）中无人机1 和无人机2 的故障估计效果Fig.4 Fault estimation result of UAV1 and UAV2 in Eq.（50）

图5 式（50）中无人机故障估计误差Fig.5 Fault estimation error of UAV in Eq.（50）

图6 式（62）控制下无人机1 相对领导者的姿态同步效果Fig.6 Attitude synchronization effect of UAV1 relative to leader under the control of Eq.（62）

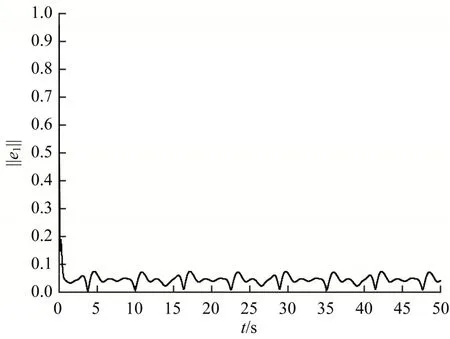
图7 式（62）控制下无人机主从式一致性误差Fig.7 Leader-follower consistency error of UAV under the control of Eq.（62）

图8 式（62）中无人机故障估计误差Fig.8 Fault estimation error of UAV in Eq.（62）

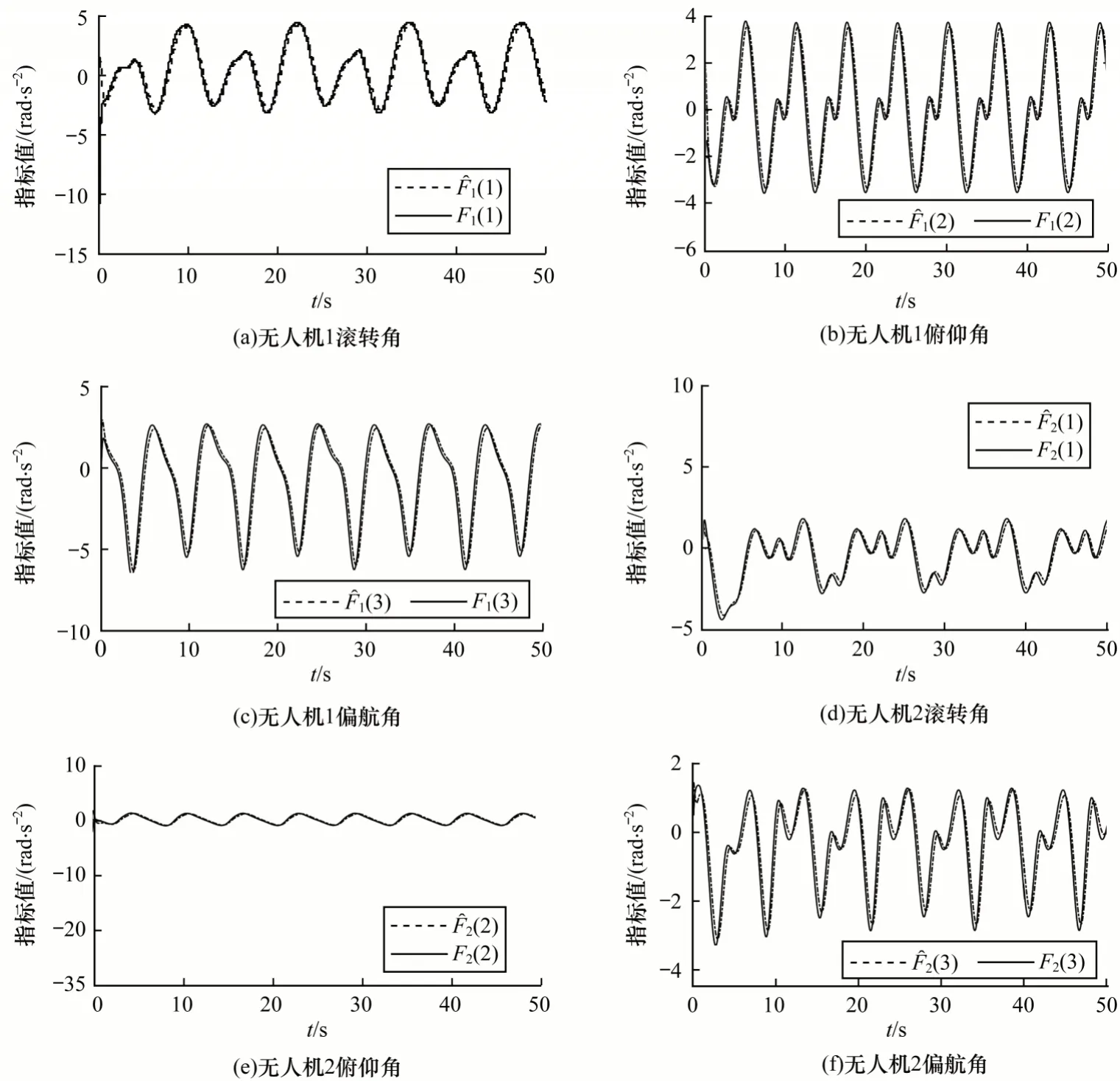
图9 式（62）中无人机1 和无人机2 的故障估计效果Fig.9 Fault estimation effect of UAV1 and UAV2 in Eq.（62）

5 结束语

本文提出一种基于观测器和神经网络的故障检测方法。该方法通过对无人机中干扰、模型不确定、状态测量误差以及控制器微小故障等集成不确定项进行快速精确估计，并在无需构造无人机实际模型的情况下，结合无人机名义模型设计一致性控制器，实现多无人机姿态对领导者的准确跟踪。下一步将在基于故障观测器的控制中引入智能控制算法，以完成无人机跟踪任务以及路径的寻优规划，满足多场景任务需求。