基于Expectimax 搜索与Double DQN 的非完备信息博弈算法

雷捷维，王嘉旸，任 航，闫天伟，黄 伟

（1.南昌大学信息工程学院，南昌 330031；2.江西农业大学软件学院，南昌 330000）

0 概述

博弈论是研究具有斗争或竞争性质现象的数学理论和方法，是经典的研究领域之一。博弈问题存在于人们生活各个方面。例如，商品定价可看作商人和顾客之间的博弈，国家之间的经济与军事竞争也可视为博弈问题。现实中博弈问题比较复杂，人们通常将其经过抽象处理转化为便于研究的游戏模型再加以解决。博弈主要分为完备信息博弈和非完备信息博弈。在完备信息博弈中，玩家可看到全部游戏状态信息，不存在隐藏信息。例如，围棋、国际象棋和五子棋等均为完备信息博弈。在非完备信息博弈中，玩家仅可看到自身游戏状态信息和公共信息，而无法获取其他游戏信息。例如，麻将、桥牌和德州扑克等均为非完备信息博弈。由于现实中许多博弈问题无法获取全部信息而被归类为非完备信息博弈，因此非完备信息博弈问题受到广泛关注。研究非完备信息博弈，可解决金融竞争［1］、交通疏导［2］、网络安全［3］和军事安全［4］等领域的问题。

近年来，关于完备信息博弈和非完备信息博弈的研究在多个应用领域取得突破性进展。在围棋应用方面，Google 公司DeepMind 团队开发出AlphaGo、AlphaGoZero 和AlphaZero 等系列围棋博弈程序，并结合蒙特卡洛树搜索与深度强化学习算法［5-7］进行实现。2016 年，AlphaGo 以4∶1 击败韩国专业围棋选手李世石引发社会关注。在德州扑克应用方面，2015 年BOWLING 等人［8］在《Science》杂志发表关于CFR+算法的论文，证明该算法已完全解决两人受限的德州扑克博弈问题。2017 年，阿尔伯塔大学开发出DeepStack系统，结合CFR 算法与多层深度神经网络（Deep Neural Network，DNN）［9］解决了德州扑克一对一无限注博弈问题。此外，人们还对《星际争霸II》等多人非合作游戏进行研究，取得众多研究成果［10-12］。

相关研究显示，麻将的复杂度要高于围棋和德州扑克［13］，然而目前关于麻将研究较少，大多数麻将程序仅基于人工经验进行设计，未结合最新的强化学习等方法。目前麻将程序设计主要采用Expectimax 搜索算法［14-15］。2008 年，林典余［16］根据Expectimax 搜索算法以赢牌最快为原则设计麻将程序LongCat。2015 年，荘立楷［17］提出转张概念对LongCat进行改进，利用所得麻将程序VeryLongCat进一步提升LongCat的赢牌效率，并赢得该年度台湾计算机博弈比赛和国际计算机博弈比赛的冠军。然而在麻将游戏中要想赢牌，除了提高赢牌效率之外，还需提高赢牌得分。目前LongCat 和VeryLongCat 的剪枝策略和估值函数均基于人工先验知识设计，由于人类经验中常存在不合理的决定或假设［18-19］，因此设计更合理的剪枝策略和估值函数成为亟待解决的问题。

为解决上述非完备信息博弈问题，本文以麻将为例进行研究。目前麻将程序主要采用Expectimax搜索算法，其计算时间随着搜索层数的增加呈指数级增长，且其剪枝策略与估值函数基于人工先验知识设计得到。本文提出一种结合Expectimax 搜索与Double DQN 算法的非完备信息博弈算法，利用Double DQN［20］算法给出的子节点预估得分，为Expectimax 搜索算法设计更合理的估值函数与剪枝策略，并将游戏实际得分作为奖励训练Double DQN网络模型以得到更高得分与胜率。

1 相关理论

1.1 Expectimax 搜索算法

Expectimax搜索树［14-15］是一种常见的搜索算法，广泛应用于非完备信息博弈游戏，其结构如图1所示。在此类游戏中，由于某些信息具有随机性和隐藏性，因此无法使用传统的minimax搜索树算法［21］来解决。针对该问题，Expectimax 搜索算法中设计了max 节点和chance 节点。其中，max 节点和chance 节点的效用值分别是其全部子节点效用值的最大值与加权平均值（即当前节点到达每个子节点的概率）。例如，对于图1中值为39 的max 节点，39 为其所有子节点（chance 节点）的最大值；对于值为14的chance节点，14为其所有子节点（max节点）的加权平均值，即：14=20×0.4+10×0.6。Expectimax 搜索算法与大多数游戏树搜索算法类似，也是通过启发式估值函数计算各节点估值。

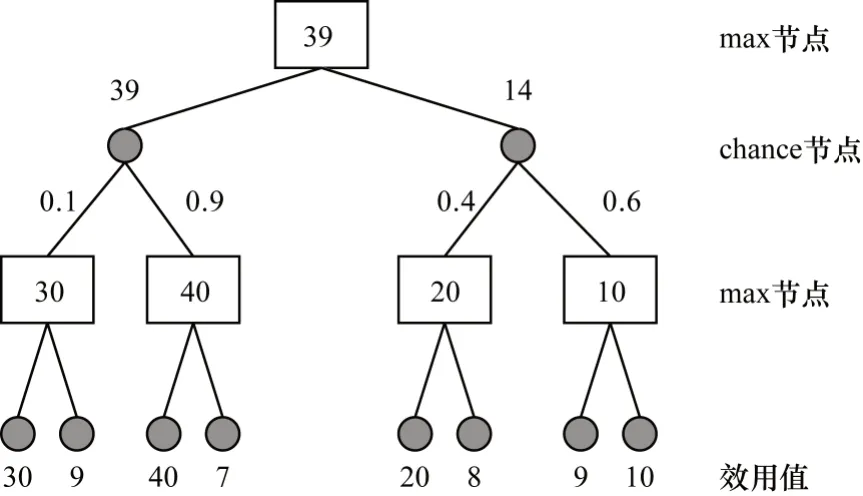
图1 Expectimax 算法的搜索树结构Fig.1 Search tree structure of Expectimax algorithm

1.2 Double DQN 强化学习算法

强化学习源于智能体对人类学习方式的模仿，是智能体通过与环境交互不断增强其决策能力的过程。强化学习算法主要包括动态规划算法［22］、时序差分算法［23］、蒙特卡洛算法［24］和Q 学习算法［25］。这些算法均存在局限性：动态规划算法虽然数学理论完备，但是其使用条件非常严格；时序差分算法可在无法获取环境全部信息的情况下得到较好效果；蒙特卡洛算法需对当前未知环境进行采样分析，由于时间与空间具有复杂性，因此其很难应用于解决时序决策问题；Q 学习算法是通过计算每个动作的Q 值进行决策，但是其存在过估计问题。

随着对强化学习研究的不断深入，研究人员对Q 学习算法改进后提出深度Q 学习算法DQN［26-27］，该算法与Q 学习算法一样，也是通过计算每个动作的Q 值进行决策，仍存在过估计问题。为解决该问题，研究人员在DQN 基础上提出双重深度Q 学习算法Double DQN［20］。

DQN 算法具有原始网络和目标网络两个神经网络，虽然其结构相同，但是权重更新不同步。DQN算法的权重更新使用均方误差（Mean Squared Error，MSE）定义损失函数，其表达式如下：

其中，a为执行动作，Rt+1为奖励分数，St为当前游戏状态信息，St+1为下一个游戏状态信息，θ为网络权重，γ为折扣因子，Q(S，a)为状态S下执行动作a的估值。

由于Q 学习算法和DQN 算法中Max 操作使用相同值选择和衡量一个动作，可能选择估计值过高的动作导致过估计问题。为此，Double DQN 算法对动作的选择和衡量进行解耦，将式（2）改写为以下形式：

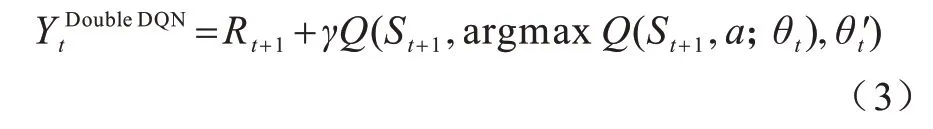
2 本文算法

2.1 基于Expectimax 搜索的麻将决策过程

由于麻将游戏过程中存在发牌随机性等不确定因素，因此其规则比较复杂。在麻将游戏中，玩家可通过捉牌、吃牌、碰牌和杠牌等方式获得一张牌，随后需再打出一张牌，后续重复上述步骤，直到游戏结束为止。如果将吃牌、碰牌和杠牌视为特殊的捉牌，则麻将中所有动作均可用序列<捉牌，打牌，捉牌，打牌…>来表示。其中，捉牌动作记录捉牌玩家的用户ID 以及捉哪张牌等信息，打牌动作记录打牌玩家的用户ID 以及打哪张牌等信息。

假设A、B、C 和D 代表4 名玩家，其中A 为当前玩家，B、C、D 为其他玩家。如果A 捉牌“9 万”后打牌“6 万”，B 碰牌“3 万”后打牌“7 筒”，A 碰牌“7 筒”后打牌“1 万”，那么上述动作序列可表示为。

实际上，如果在决策中考虑所有玩家的动作，则Expectimax 算法的搜索树很大，从而无法在有限时间内做出决策。为解决该问题，通常将整个游戏博弈过程进行抽象处理，仅考虑当前玩家的捉牌与打牌动作，并以此构建Expectimax 算法的搜索树。此外，为进一步简化搜索树，将吃牌、碰牌和杠牌也作为特殊的捉牌，则上述动作序列表示为。

通过上述方法，本文将麻将游戏过程简化为捉牌和打牌两个动作。结合Expectimax 搜索算法，将捉牌动作看作chance 节点，打牌动作看作max 节点。例如，假设当前玩家手中持有的牌（以下称为手牌）为1 万、2 万、4 万、9 万和9 万，那么基于Expectimax算法的麻将搜索树结构如图2 所示。

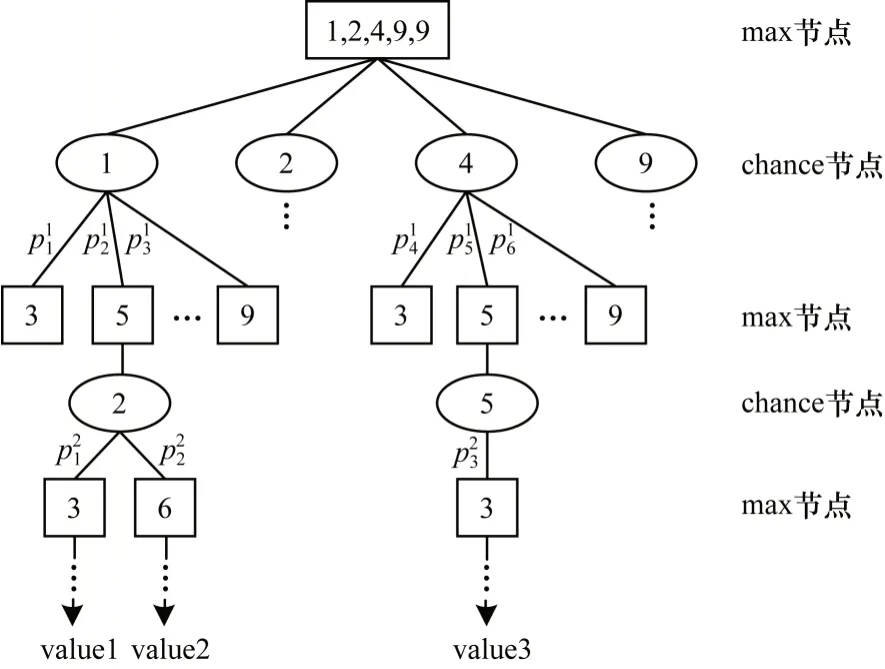
图2 基于Expectimax 算法的麻将搜索树Fig.2 Mahjong search tree based on Expectimax algorithm

在图2 中：max 节点表示打牌节点；chance 节点表示捉牌节点；将“打牌节点，捉牌节点”作为搜索树的一层；value 值表示游戏结束时当前游戏树分支获得的分数表示当前第i层捉牌节点（父节点）转移到第j个打牌节点的概率。计算公式如下：

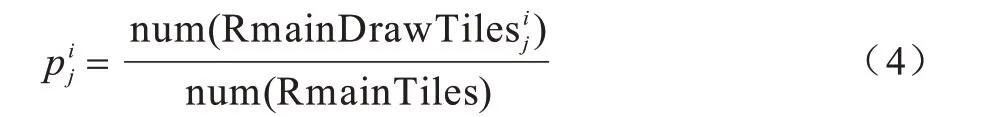
其中，num(RmainTiles)表示牌库中剩余牌的数量，表示使第i层捉牌节点转移到第j个打牌节点的麻将牌。而表示该麻将牌在牌库中的剩余数量。由图2 和式（4）可计算出每个捉牌节点与打牌节点的值。

捉牌节点的值等于其所有子节点分数的加权平均值，计算公式为：

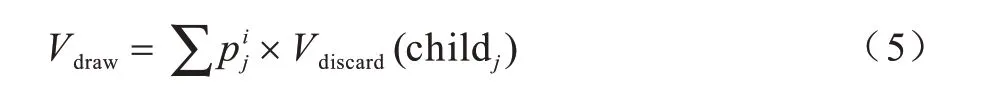
打牌节点的值等于其所有子节点的最大分数，计算公式为：

在有限时间内通常无法完全搜索整个游戏树，为使算法能在限定时间内响应，主要采取两种方法：1）限制搜索树深度并用估值函数评估当前节点的值；2）设计一种合理的剪枝策略对游戏树进行剪枝。由于Expectimax 搜索算法的估值函数与剪枝策略均基于人工先验知识而设计，因此该算法的决策水平在很大程度上取决于设计者对麻将的理解。为摆脱人工先验知识的局限性，进一步提高算法决策水平，本文结合Double DQN 算法对传统的Expectimax 搜索算法进行改进。

本文将Double DQN 算法所用神经网络设为fθ。其中，参数θ表示神经网络的权重，神经网络的输出是一个34 维的数据，表示34 种出牌对应的分数（Q值）。

1）对Expectimax 搜索算法中剪枝策略进行改进，如图3 所示。对于当前玩家的手牌，可通过神经网络fθ(S)计算每个打牌动作对应的Q值。

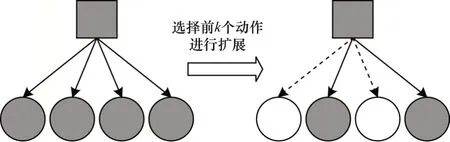
图3 改进Expectimax 搜索算法的剪枝策略Fig.3 The pruning strategy of the improved Expectimax search algorithm

在搜索树扩展的过程中，先通过神经网络的估值对所有打牌动作从大到小进行排序，再将前k个动作扩展为子节点，余下动作不再扩展，从而达到剪枝的目的。k值的计算公式如下：

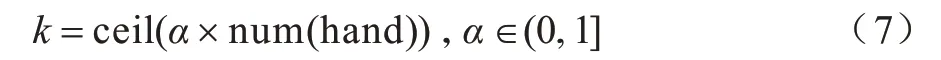
其中，num(hand)表示当前玩家手牌的牌数。由于神经网络能估算出每个动作的Q值，因此通过为每个动作的Q值排序，只扩展前k个动作来减小搜索树的广度，从而实现对搜索树剪枝，使计算机在有限时间内将更多时间用于搜索树的深度扩展。

2）改进Expectimax 搜索算法的估值函数，如图4所示。若麻将搜索树某个分支在限定搜索层数内能到达游戏结束状态并获得分数，则将该分支的值设置为游戏实际分数；否则需设计合理的评估函数，并将其估值作为该分支的值。

图4 改进Expectimax 搜索算法的估值函数架构Fig.4 Evaluation function architecture of the improved Expectimax search algorithm

传统Expectimax 搜索算法的估值函数大部分是基于人工先验知识而设计，存在不合理的决定或假设。本文采用Double DQN 神经网络的Q值解决该问题。如果麻将搜索树的一个分支在限定搜索层数内无法到达游戏结束状态，则可通过神经网络计算当前节点的Q值作为该分支的值，即：构造一个打牌节点，再根据神经网络计算出每个动作的Q值，并选择最大的Q值max(Q) 作为该分支的值。改进Expectimax 搜索算法的估值函数架构如图4 所示。

2.2 基于Double DQN 的麻将模型训练过程

2.2.1 基于麻将先验知识的特征编码

在麻将游戏中，由于当前玩家对其他玩家的手牌以及牌库内的牌不可见，因此麻将是典型的非完备信息博弈游戏，如何只根据游戏部分信息进行正确决策是需要考虑的问题。

以下介绍基于麻将先验知识的特征编码，如表1所示。这些特征包括当前玩家的手牌、当前玩家的副露、其他玩家的副露、所有玩家的弃牌以及游戏轮数等。基于麻将相关先验知识可描述当前游戏全部可见信息，从而加快麻将模型训练速度。本文使用ResNet 网络［28］模型进行训练，因此，需要将特征重塑为二维矩阵，即以填零的方式将特征向量转换为19×19的二维矩阵，并将其输入到ResNet 网络。

表1 基于麻将先验知识的特征编码Table 1 Feature coding based on mahjong prior knowledge

2.2.2 Double DQN 麻将模型的训练过程

图5 为结合Expectimax 搜索算法的Double DQN网络模型训练过程，其具体步骤如下：

1）获取游戏中当前玩家的手牌、当前玩家的副露、其他玩家的副露、所有玩家的弃牌、游戏轮数、牌库剩余牌数等全部可见信息。

2）根据麻将的先验知识，将可见信息编码为特征数据。

3）将编码后的特征数据输入Double DQN 神经网络，从而获得每个动作的估值。

4）基于每个动作的估值，使用改进的Expectimax搜索算法精确计算出具有最高得分的推荐动作，然后执行该动作。

5）动作执行完毕即可获得下一个游戏状态信息与该动作的奖励分数。

6）根据执行动作、奖励分数、当前游戏状态信息和下一个游戏状态信息，结合梯度下降算法对Double DQN神经网络进行训练后得到麻将强化学习模型。其中，梯度下降算法在Double DQN 神经网络中需最小化的损失函数如式（1）所示，Double DQN 算法中Y值按照式（3）进行计算。

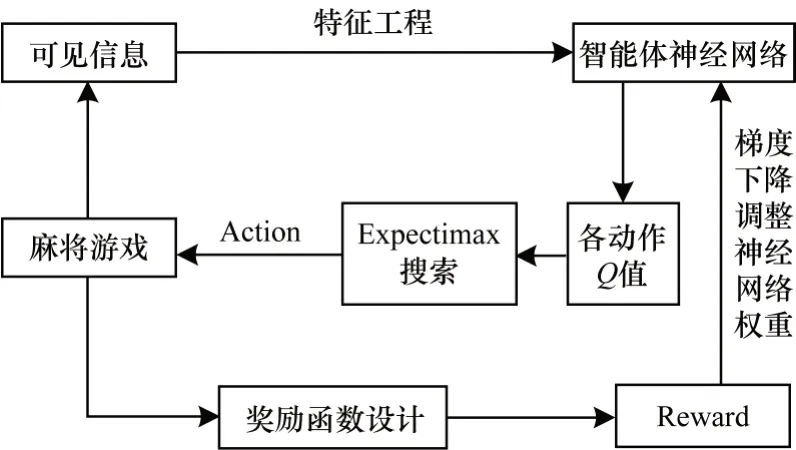
图5 Double DQN 麻将模型的训练过程Fig.5 Training procedure of Double DQN mahjong model

由于麻将游戏在结束时才能获得奖励分数，在游戏期间没有任何奖励，因此麻将是一种典型的奖励稀疏游戏。为改变这一状况，本文设计奖励函数如下：

其中，VExpectimax为通过Expectimax 搜索算法计算得到的推荐动作效用值。在式（8）中，将游戏结束时实际得分设置为模型的奖励，并将游戏中的奖励设置为0.1×VExpectimax。

由上述可知，Expectimax 搜索算法使用Double DQN 神经网络输出的Q值来设计剪枝策略与评估函数。而在强化学习模型训练过程中，使用Expectimax 搜索算法改进Double DQN 算法的探索策略与奖励函数。在该过程中，Double DQN 算法和Expectimax 搜索算法相互结合与促进，进一步提高麻将模型的决策水平。

3 实验与结果分析

3.1 数据描述和数据预处理

将本文算法与其他监督学习算法进行对比，并讨论参数α的设置对模型的影响。实验环境为：3.6.5 Python，1.6.0 tensorflow，GTX 108 显卡，16 GB RAM 内存以及Ubuntu 16.04 系统。从某麻将游戏公司筛选大量高水平玩家的游戏数据（只筛选游戏得分排名前1 000 的玩家游戏记录，且每位玩家至少已赢得500 场比赛）对监督学习算法的网络模型进行训练，共筛选出360 万条游戏数据，按照数量比例3∶1∶1 将数据分为训练集、测试集和验证集，并根据表1 中特征编码处理数据。值得注意的是，对于CNN、DenseNet 和ResNet 等具有卷积层结构的网络模型，需采用填零的方式将特征转换为19×19 的二维矩阵。

3.2 对比实验

将本文提出的Expectimax搜索+Double DQN算法（以下称为本文算法）与线性分类（Linear）、支持向量机（SVM）［29］、FC［30］、CNN、DenseNet-BC-190-40［31］、ResNet-1001［32］、DQN、Double DQN 以及Expectimax 搜索等算法进行对比。其中，DQN、Double DQN 和本文算法（以下称为第1 类算法）均使用20 层的ResNet作为神经网络。为便于比较，上述算法实验参数设置相同，如表2 所示。

表2 第1 类算法的实验参数设置Table 2 Experimental parameter setting of the first kind of algorithm

对于Linear、SVM、FC、CNN、DenseNet、ResNet-1001算法以及本文算法中的Expectimax搜索部分（第2类算法），相关参数设置如表3所示。其中，参数α采用多次实验得到的最佳值（关于参数α设置的讨论见3.3节）。

表3 第2 类算法的实验参数设置Table 3 Experimental parameter setting of the second kind of algorithm

本文采用台湾麻将游戏平台进行实验。与大部分麻将游戏不同，台湾麻将在开局时，每位玩家持有16 张牌，且有花牌等特殊牌型。台湾麻将赢牌的方式较简单，只有平胡，但其得分计算较复杂，计算公式如下：

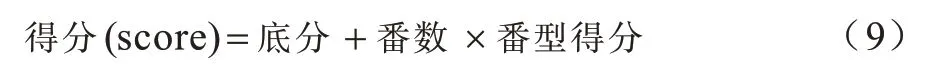
其中，底分与番型得分需要玩家在游戏开始前设置，番数取决于玩家最后赢牌时的牌型，例如清一色、四暗刻等。本文排除台湾麻将中的花牌来简化游戏流程，将底分和番型得分分别设置为1 000 和500，使用2对2 的形式进行3 000 场4 人台湾麻将比赛。在对局中，采用两个算法为基准算法，另外两个算法为实验算法，同时轮流交换不同玩家的相对位置以确保游戏的公平性。将不同实验模型与基准模型进行对比来分析其优劣性。

本文实验使用Expectimax搜索算法作为基准算法，上述不同算法的实验结果如表4 所示。可以看出本文算法在对比实验中表现最佳。对比ResNet-1001 和其他监督学习模型可知，随着模型复杂度的提高，监督学习模型决策水平也相应提升。但是横向比较后发现，监督学习算法不如强化学习算法和Expectimax 搜索算法，这是因为监督学习算法的网络模型是通过收集用户数据进行训练，尽管已设置标准来筛选高水平玩家的游戏数据，但仍然无法保证数据质量，而强化学习算法和Expectimax 搜索算法的网络模型无需用户游戏数据进行训练，可避免人类先验知识造成的偏误。

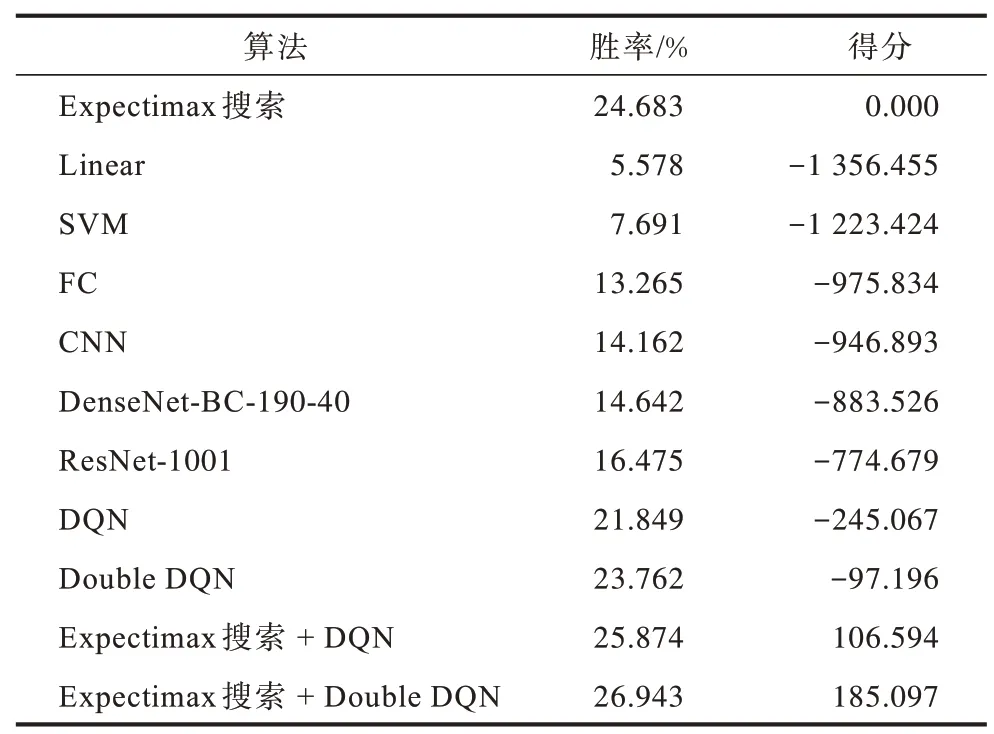
表4 不同算法的实验结果Table 4 Experimental results of different algorithms

由表4 还可以看出：Double DQN 算法的性能优于DQN 算法，这是因为Double DQN 算法改善了DQN 算法的过估计问题；本文算法比Expectimax 搜索+DQN 算法的表现更好；本文算法的胜率比Expectimax 搜索算法高出2.26 个百分点，平均每局得分多185.097 分，这是因为本文算法将Expectimax搜索算法与强化学习算法Double DQN 相结合，在游戏训练过程中不断迭代优化，从而提高胜率和得分。

3.3 参数α 的设置对模型的影响

本文在3.1节提出根据k值对搜索树进行剪枝的策略，由式（7）可知k值取决于参数α的设置。以下分别从耗时、胜率和得分讨论参数α对本文算法的影响。

将参数α分别设置为0.2、0.4、0.6、0.8 和1.0，搜索树限定层数分别设置为1 层和2 层，比较不同搜索层数下α值大小对本文算法的耗时、胜率和得分3 个方面的影响，结果如表5～表7 所示。

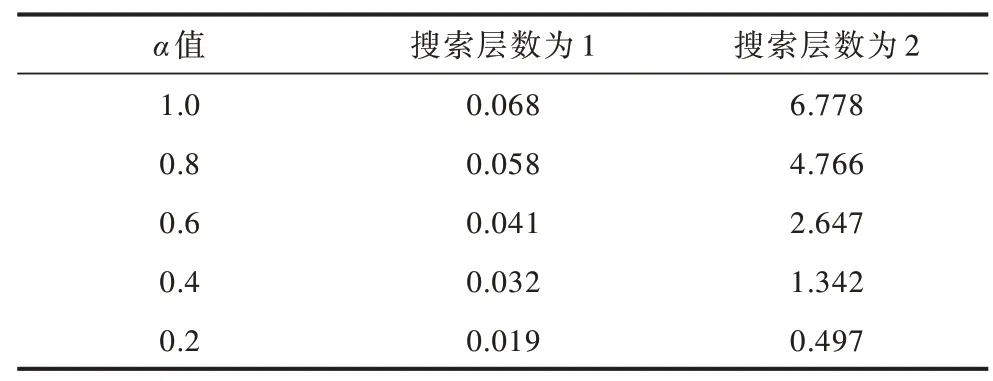
表5 参数α 对算法耗时的影响Table 5 Influence of parameter α on the time consumption of the algorithms

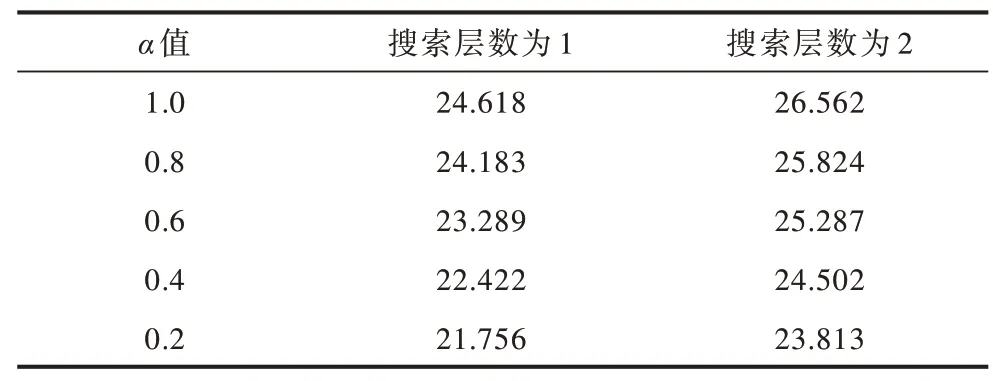
表6 参数α 对算法胜率的影响Table 6 Influence of parameter α on the winning rate of the algorithm%

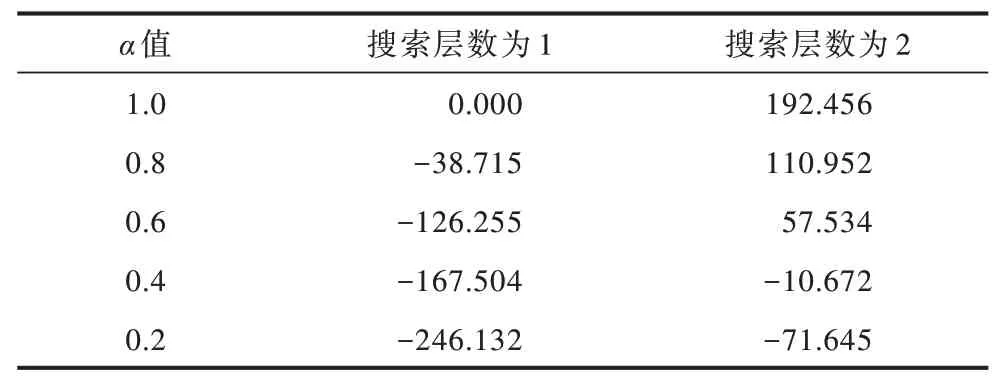
表7 参数α 对算法得分的影响Table 7 Influence of parameter α on the score of the algorithm

在表5 中，当参数α设置为1.0 时，相当于完全展开整个搜索树，此时算法在搜索层数为1 和2 时决策时间分别为0.068 s 和6.778 s。可以看出，如果不修剪搜索树，则决策时间会呈现指数级增长，因此，需要合理地对搜索树进行剪枝从而减少算法耗时。由表5 还可以看出，随着α值的减小，算法在不同搜索层数下决策时间不断减少。由表6 和表7 可以看出，随着搜索层数的增加，本文算法的胜率和得分相应增加，而结合表5 可知算法的耗时随着搜索层数增加也在增长。因此，为使算法在3 s 内做出响应，本文算法选取α=0.6 且搜索层数为2。

4 结束语

麻将作为典型的非完备信息博弈游戏，主要通过Expectimax 搜索算法实现，而该算法中剪枝策略与估值函数基于人工先验知识而设计，存在不合理的假设。本文提出一种结合Expectimax搜索与Double DQN 的非完备信息博弈算法。利用Double DQN 强化学习算法改进Expectimax 搜索树的剪枝策略和估值函数，并通过Expectimax 搜索改进Double DQN 模型探索策略与奖励函数。实验结果表明，与Expectimax 搜索算法相比，该算法在麻将游戏上胜率提高2.26 个百分点，平均每局得分增加185.097 分。由于本文算法剪枝策略中参数α需借助人工先验知识来选择，因此后续将使用自适应方法进行改进，以提高算法的准确性。