基于多特征和尺度估计的KCF_MTSA 算法
尚桠朝,孟令军
(中北大学电子测试技术国家重点实验室,太原 030051)
0 概述
目标跟踪作为计算机视觉的重要组成部分,被广泛应用于交通安全[1]、自动驾驶[2]和行为识别[3]等领域。然而在实际应用场景中,由于目标常出现形变、遮挡和快速移动等情况,造成跟踪效果急剧下降,因此提高复杂情况下的目标跟踪精度和成功率具有重要意义[4]。
相关滤波器算法因具有跟踪精度高和速度快的特性成为目标跟踪的研究热点之一[5-6]。文献[7]提出一种使用方向梯度直方图(Histogram of Oriented Gradient,HOG)特征的核相关滤波器(Kernelized Correlation Filter,KCF)跟踪算法,引入循环矩阵和核函数使该算法在保持高帧率的情况下跟踪精度得到极大提升。文献[8]提出一种SAMF 算法将多种特征进行融合,在定位目标的同时求解最佳目标尺寸。文献[9]提出判别尺度空间跟踪(Discriminative Scale Space Tracker,DSST)算法,通过引入一维相关滤波器完成目标尺度估计。上述算法求解滤波器时会忽略目标的历史信息,对此,文献[10]提出多模板尺度自适应核相关滤波器(Kernelized Correlation Filter based on Multiple-Template Scale Adaptation,KCF_MTSA)跟踪算法,同时更新历史模板信息与当前模板信息来求解滤波器,从而实现滤波器的时间一致性。文献[11]提出Staple 算法,将方向梯度直方图特征与颜色直方图特征进行融合,有效提升算法性能。文献[12]提出背景感知相关滤波器(Background-Aware Correlation Filter,BACF)算法,利用掩膜矩阵获取正负样本建立目标模板,在实现高精度的同时确保高速率。随着深度学习的兴起,文献[13-14]利用卷积神经网络进行跟踪目标的特征提取,特征辨识度更高,算法性能得到较大提升,但是其计算开销较大,在实际应用中难以满足实时跟踪的要求。
针对KCF_MTSA 算法提取特征单一与尺度策略较简单的问题,本文提出一种改进的多模板尺度自适应核相关滤波器跟踪算法。通过方向梯度直方图和颜色名(Color Name,CN)表征目标特征,在决策层对两种特征的响应进行自适应融合以实现目标定位,同时引入一维相关滤波器进行尺度估计,并计算多尺度样本信息中尺度滤波器的响应,从而得到当前目标的最佳估计尺寸。
1 KCF_MTSA 算法
1.1 分类器训练
在KCF 算法中,利用非线性映射函数φ(x)使映射后的样本在高维空间线性可分,在新空间使用岭回归[15]方法对回归函数f(x)=wTx训练如下:
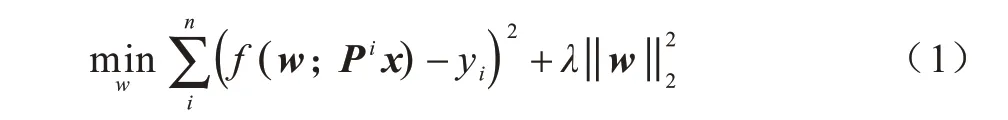
其中,Pi为循环移位算子,x为基础样本,Pi x为基础样本x循环右移i个单位,yi为对应样本的期望输出。
上述目标函数可改写为:

其中,Φ为包含样本x所有循环移位样本的映射。在KCF_MTSA 算法中,将训练滤波器中样本扩展到2 个,假设在第n帧滤波器训练中目标模板为xn,其循环矩阵为Xn,则KCF_MTSA 算法的目标函数为:
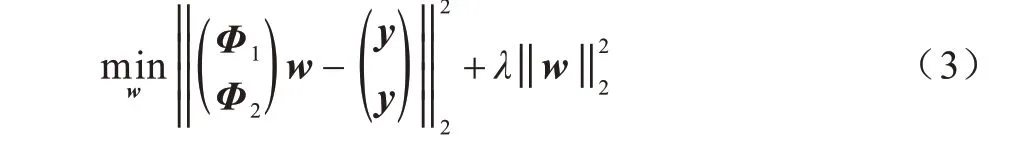
其中,Φ1和Φ2为上一帧目标模板x1和当前帧目标模板x2的循环移位样本的映射矩阵。Φi为循环矩阵,通过引入一个辅助变量分别对两个目标模板进行滤波器求解,并加入一个约束使两个目标模板所求滤波器相等,表达式如下:
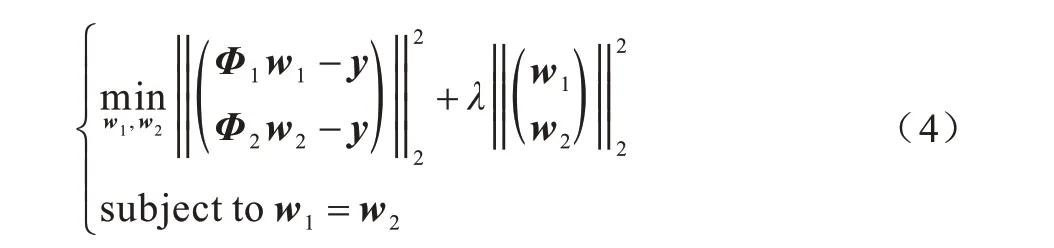
上述问题可通过将硬约束换成软约束求解,引入正则项如下:

式(5)中额外的正则项可确保两个滤波器的一致性。在每次迭代过程中,参数μ不断增大,且每次迭代通过交替定点来优化问题:首先初始化滤波器w2,再利用其优化另一个滤波器w1,然后利用滤波器w1求解滤波器w2,如此进行多次循环直到满足迭代要求。使用单模板的核相关滤波器进行滤波器初始化,在第j次迭代过程中,求解对偶问题如下:
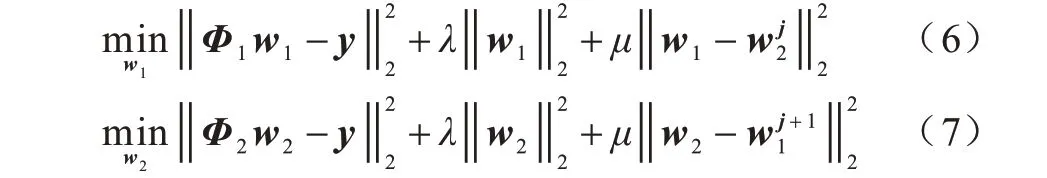
由于式(6)和式(7)形式相同,因此求解其中任意一个即可。将式(6)改写为多特征核函数如下:

1.2 目标位置检测
KCF_MTSA 目标位置检测和尺度估计同时进行,以上一帧检测到的目标中心点为中心,在当前帧图像中建立尺度池,采样n个尺度,计算每个尺度图像的响应,第i个尺度图像响应的计算公式如下:

其中,zi为第i个尺度的样本,x为上一次跟踪完成后更新的模板为的离散傅里叶变换为多模板核相关滤波器参数。通过计算最大响应值的位置可得到目标的中心和尺寸。
1.3 模板更新
完成目标位置的定位与尺度估计后,更新目标模板和滤波器参数如下:

其中,η为学习率分别为第t帧目标模板和第t-1 帧目标模板,Xt为未更新的第t帧目标模板,为第t帧滤波器参数。
2 改进的KCF_MTSA 算法
2.1 互补特征自适应双核融合
本文使用方向梯度直方图和颜色名双核融合的方式进行目标定位。HOG 特征通过计算和统计图像局部区域的梯度方向直方图构成特征,对光照和目标的几何变换不敏感;CN 特征具有光照不变性,对目标大小和形变不敏感,但是在光照剧烈变化的情况下无法准确表征目标[16-17]。在复杂场景下,采用自适应特征融合的方式通过HOG 和CN 特征来表征目标,可实现目标跟踪。
提取上述特征,并分别计算两种特征的滤波器响应如下:

其中,xhog和xcn分别为当前帧图像目标区域内的HOG 特征和CN 特征,zhog和zcn分别为上一帧图像目标模板更新后的HOG 特征和CN 特征分别为上一帧图像求解的HOG 特征多模板核相关滤波器参数的离散傅里叶变换和CN 特征多模板核相关滤波器参数的离散傅里叶变换。
在特征融合方面,使用两个多模板核相关滤波器,将每种特征获得的响应以权重形式进行融合如下:

在式(19)中,whog由HOG 特征获取响应图的峰值旁瓣比(Peak to Side Lobe Ratio,PSR)和CN 特征获取响应图的PSR 共同决定,计算公式如下:

PSR 可作为跟踪结果的评价指标,该值越大,跟踪结果越可靠[18]。

式(20)中P的计算公式如下:其中:q为响应图的峰值,峰值周围区域为旁瓣区域;u和σ分别为旁瓣区域的平均值和标准差。通过计算获得融合后的响应图,其峰值位置即为目标位置。
2.2 一维相关滤波器尺度估计
由于KCF_MTSA 算法的尺度估计方法与SAMF 算法类似,两者对尺度的估计均不理想,因此本文算法引入一维相关滤波器进行尺度估计[19]。假设当前图像为In,目标尺寸为P×R,对图像In提取训练样本,其中心为目标位置,样本的尺寸表达式如下:

采用岭回归的方式训练样本并计算尺度滤波器,目标函数为:
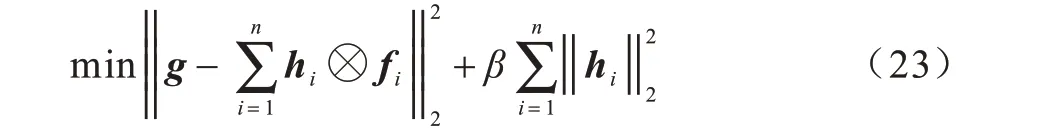
其中,⊗为相关算子,g为一维高斯函数,hi和fi分别为第i个尺度的滤波器和样本,β=0.01 为正则化参数。
根据Parseval 定理,将目标函数转换到频域进行求导,令导数为0,计算得到:
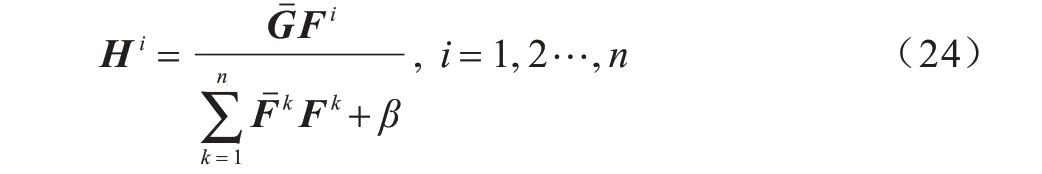
其中,大写字母变量代表响应小写字母变量的离散傅里叶变换,为G的共轭形式。
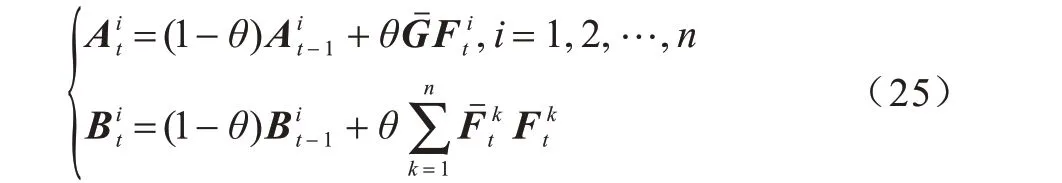
其中:θ为学习率,本文中θ=0.025分别表示当前帧的分子与分母分别表示上一帧的分子与分母。
对于第t帧样本Z,建立尺度池(i=1,2,…,n)并进行相应尺度滤波器的计算,相关公式如下:

其中,Γ-1为离散傅里叶的逆变换。通过计算尺度滤波器的响应可得到当前目标的最佳估计尺寸。
2.3 FMMTSA_DSST 算法
本文对KCF_MTSA 算法进行改进后提出FMMTSA_DSST 算法,在该算法中目标定位和尺度估计各自独立进行。在目标定位过程中,使用两个核相关滤波器实现目标定位;在尺度估计过程中,先建立尺度池,再使用相关滤波器求解以完成目标尺度估计,并将最佳尺度参数传递到两个核相关滤波器的训练和尺度相关滤波器的训练中,具体步骤如下:
1)快速检测:
(1)输入第t(t>1)帧图像,根据上一帧图像目标中位置Dt-1和尺寸参数St-1截取候选样本的HOG 特征zhog和CN 特征zcn。
(2)根据式(17)~式(19)求得目标定位用响应,再对R进行离散傅里叶逆变换获取目标的新位置Dt。
(3)以Dt为中心位置、St-1为基础目标尺寸,根据式(22)构建尺度池(i=1,2,…,n)。由式(26)计算得到尺度滤波器的响应,其最大值为当前目标最佳尺度估计St。
2)训练分类器:
(1)以当前目标中心位置Dt和最佳尺度St为参数,截取HOG 特征目标模板xhog和CN 特征目标模板xcn,根据式(14)迭代计算得到ahog和acn。
(3)以当前目标中心位置Dt和最佳尺度St为参数,根据式(22)构建尺度池(i=1,2,…,n),通过式(25)计算完成尺度滤波器的更新。
(4)如果为最后一帧,则训练结束;否则依次执行快速检测与训练分类器中的全部步骤。
3 实验与结果分析
3.1 实验方法
为验证本文所提FMMTSA_DSST 算法(以下称为本文算法)的有效性,在OTB100[20]数据集中选取25 组视频序列进行实验,其中包括尺度变化、光照变化、运动模糊、平面旋转和遮挡等属性。将本文算法与ECO_HC、STAPLE_CA[21]、SAMF_AT[22]、KCF、KCF_MTSA和SAMF 算法进行对比。实验采用Ubuntu18.04 系统和MATLAB2016a 软件平台,计算机配置Intel®XeonTMCPU E5-2697 v2 @ 2.70 GHz 处理器和RTX2070 显卡。
3.2 结果分析
中心误差(Center Location Error,CLE)是算法跟踪到的目标位置与人工标注目标位置的欧氏距离,若CLE 小于某个阈值(本文中CLE 阈值设置为20),则跟踪成功;否则跟踪失败。距离精度(Distance Precision,DP)为CLE 小于某个阈值的视频帧数占总视频帧数的比例。重叠率(Overlap Rate,OR)为算法跟踪到的目标边界框与人工标注边界框重合部分占整个目标边界框的比例,若OR 小于某个阈值(本文中OR 阈值设置为0.5),则跟踪成功;否则跟踪失败。重叠分数(Overlap Score,OS)为算法跟踪过程中OR 小于某个阈值的视频帧数占总视频帧数的比例,以此作为准确率的评价指标。为对上述算法进行定量分析,使用DP 和OS 作为算法跟踪性能的评价指标。
图1~图4 分别为7 种算法的综合评价结果以及在目标旋转、尺度变化和运动模糊情况下的评价结果(图1(a)~图4(a)中的中括号内数字为算法在重叠率阈值为0.5 时的准确率,图1(b)~图4(b)中的中括号内数字为算法在中心误差阈值为20 时的距离精度)。可以看出:本文算法综合评价的准确率和距离精度均排在第二位,较改进前KCF_MTSA 算法的准确率和距离精度分别提升28.5% 和15.8%;ECO_HC 算法由于引入卷积神经网络,因此其综合评价结果较其他算法更好;本文算法在目标旋转和尺度变化情况下的准确率和距离精度均排在前两位,较改进前KCF_MTSA 算法有明显提升,且在目标出现旋转时其跟踪性能最佳。
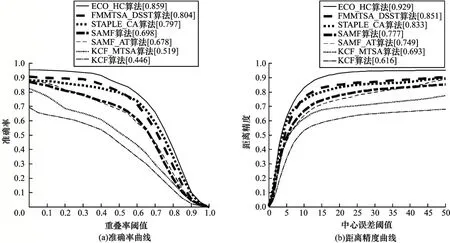
图1 7 种算法的综合评价结果Fig.1 Comprehensive evaluation results of seven algorithms

图2 7 种算法在目标旋转时的评价结果Fig.2 Evaluation results of seven algorithms when the target rotates
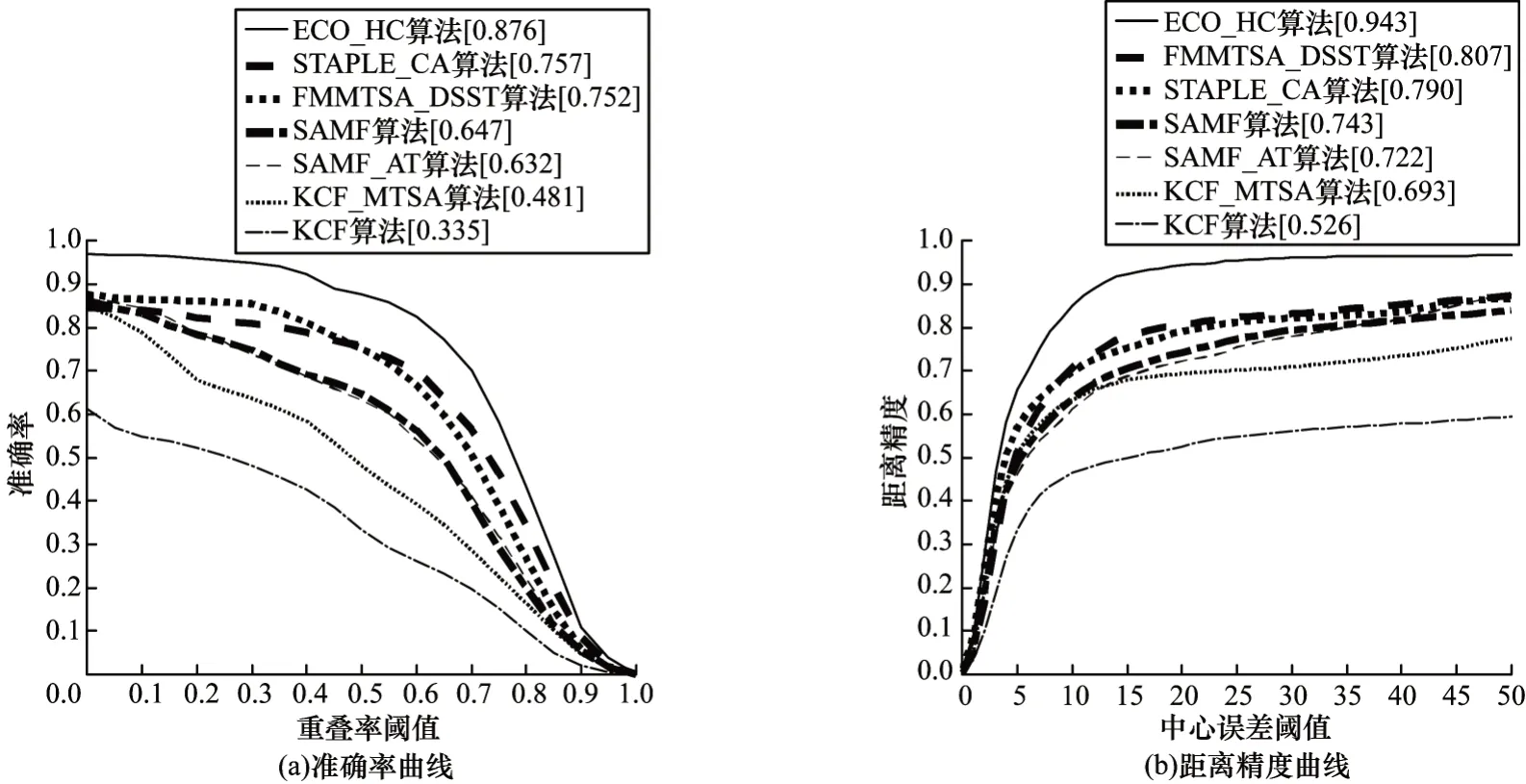
图3 7 种算法在尺度变化时的评价结果Fig.3 Evaluation results of seven algorithms when the scale changes

图4 7 种算法在目标运动模糊时的评价结果Fig.4 Evaluation results of seven algorithms when the target is blurred by motion
将上述算法在不同属性数据集中处理速度的平均值作为算法的处理速度进行对比,结果如表1 所示。可以看出:本文算法由于引入CN 特征并应用尺度估计策略,因此处理速度较KCF_MTSA 算法更慢,但仍快于SAMF_AT 算法和STAPLE_CA 算法,结合图1~图4分析结果可知,本文算法跟踪效果更好;ECO_HC 算法处理速度较快,可满足算法的实时性要求,其跟踪性能也最好。

表1 7 种算法的处理速度对比Table 1 Comparison of processing speed of seven algorithms(frame·s-1)
为更直观地验证本文算法的跟踪效果,将7 种算法在BlurBody、Human7、KiteSurf、Panda、CarScale、Human6、BlurOwl 和Shaking 8 个视频序列中的跟踪结果进行对比,结果如图5 所示。可以看出:上述算法在BlurBody、Human7 和BlurOwl 视频序列中均存在由镜头晃动造成运动模糊的问题;随着运动模糊程度的加剧,仅用HOG 特征的KCF 算法和KCF_MTSA 算法最先出现定位误差增大现象,其他算法均实现目标的准确跟踪;当KiteSurf 视频序列第42 帧目标出现旋转和快速移动时,仅本文算法和STAPLE_CA 算法可跟踪到目标,SAMF 算法在64 帧重新跟踪到目标,ECO_HC、SAMF_AT、KCF 和KCF_MTSA 算法均出现跟踪丢失现象;在Panda 视频序列中,目标熊猫在第100 帧第1 次转身导致KCF算法出现目标定位框偏移,目标熊猫在第490 帧再次转身,KCF 和KCF_MTSA 算法完全丢失目标,目标熊猫在第633 帧第3 次转身后,仅本文算法和ECO_HC 算法可继续进行目标跟踪;当CarScale 视频序列第225 帧目标尺度迅速变化时,虽然SAMF算法也有尺度估计策略,但是仅STAPLE_CA、ECO_HC 算法和本文算法能实现较好的跟踪效果;Human6 视频序列在第245 帧将镜头拉近使得目标尺寸变大,此时本文算法可很好地对边界框定位,而SAMF 算法和SAMF_AT 算法由于所用尺度样本较少,尺度估计效果较差,SAMF、SAMF_AT 和KCF 算法在第497 帧丢失跟踪目标;Shaking 视频序列在第25 帧出现背景杂波,此时仅本文算法和ECO_HC 算法完成目标跟踪,且在第61 帧出现光照变化时,上述两种算法跟踪效果未下降,在第71 帧和第150 帧目标旋转后,本文算法仍能完成目标跟踪任务。

图5 7 种算法在8 个视频序列中的跟踪效果Fig.5 Tracking effect of seven algorithms in eight video sequences
4 结束语
本文针对KCF_MTSA 算法在目标移动模糊、旋转和尺度变化时跟踪精度下降的问题,在KCF_MTSA算法基础上,提出一种结合多特征和尺度估计的改进目标跟踪算法。使用互补特征HOG+CN 进行目标表征,根据响应图的峰值旁瓣比将两种特征的响应进行自适应融合,同时引入一维相关滤波器进行尺度估计。实验结果表明,与改进前KCF_MTSA 算法相比,该算法的跟踪距离精度和准确率明显提升,在目标尺度变化较大时,能很好地完成目标尺度估计,有效避免尺度估计不准确导致背景信息引入时目标偏移的问题。后续将利用神经网络提取特征实现目标跟踪,进一步提升跟踪距离精度。

