一类六阶非线性发展方程的整体吸引子
袁 爽,段 宁
(东北大学 理学院,辽宁 沈阳 110819)
1 引言与预备知识
过去的几十年里,在力学和物理学中有着广泛应用的六阶非线性发展方程越来越引起偏微分方程学者们的注意.迄今为止,已经有许多经典文献对六阶非线性发展方程进行了研究[1-4].
在研究固体基底上生长的薄膜时,Golovin 等人[5]提出了一类描述薄膜自由表面连续演化的经典表面扩散方程:

这里:vn是法向表面速度,ϑ=DSS0Ω0V0/(RT)23(DS是表面扩散率,S0是表面每单位面积的原子数,Ω0是原子体积,v0是薄膜中晶格的摩尔体积,R是通用气体常数,T是绝对温度),ΔS是表面拉普拉斯算子,v是测量边角能量的正则化系数,Cαβ是表面曲率张量,μw是u的指数衰减函数,其奇点在u→0.本文主要研究的是在小斜率近似中,具有立方对称性和高对称性取向晶体的情况下膜厚的发展方程,该方程具有如下形式[6]:
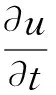
(1.1)

(1.2)
我们对u和阶数≤5的u的导数附加以下周期性边值条件:
φ|xi=0=φ|xi=Li,i=1,2,3,4,5,
(1.3)
和初始条件
u(x,0)=u0(x),x∈[0,1]
.
(1.4)
在文献[6]中,Zhao对方程(1.1)解的正则性进行了研究.作者利用Schauder型估计和Campanato空间的相关性质,证明了具Neumann边界条件的方程(1.1)古典解的存在性.在这里,我们研究问题(1.1)-(1.4)解的长时间行为,证明其整体吸引子的存在性等问题.
首先需指出,问题(1.1)-(1.4)的解是满足质量守恒的,即:

从而,可给出整体弱解的存在性引理:

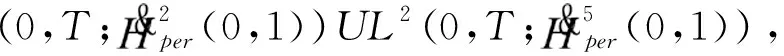

下面给出本文的主要定理:

2 解的一致估计


其中:M0是依赖k,v的正常数,T0是依赖k,v和R的正常数.
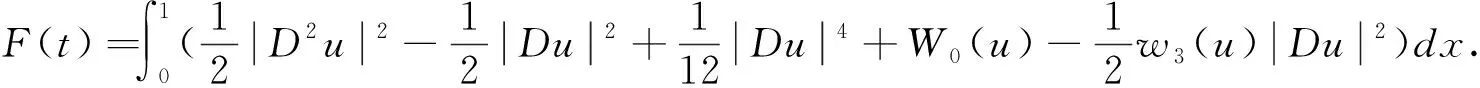
对上述等式两边同时对x求导,根据周期性边值条件,可得


从而
(2.1)
由Poincaré不等式得
(2.2)
联立(2.1)和(2.2),我们有

(2.3)
由(2.2),(2.3)和Poincaré不等式可知
(2.4)
进一步,由Sobolev嵌入定理可得

对(1.1)两边同乘D4u,关于x在(0,1)上积分,可得:





由Nirenberg不等式和Young不等式得:


同理,可得

从而,进一步由Young不等式和Hölder不等式可得:

综上所述,我们有
当ε'足够小满足1-8ε'>0,得

(2.5)



其中:M1是依赖k,v的正常数,T1是依赖k,v和R的正常数.
证明方程(1.1)两边同乘D6u,关于x于(0,1)上积分可得





由Nirenberg不等式和Young不等式可得

同理,可得:


由Young不等式和Hölder不等式可得:

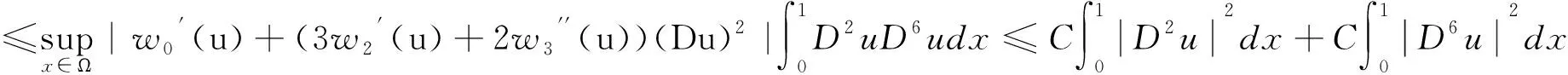

综上所述,可得
(2.6)


由Sobolev嵌入定理得||D2u||∞≤C9.
令t≥T1,取s∈(t,t+1),对(2.6)在(s,t+1)上积分,可得
||D3u(t+1)||2≤C10+||D3u(s)||2.
对上述不等式,关于s于(t,t+1)上积分,得:

对方程(1.1)两边同乘ut,且关于x于(0,1)上积分,可得



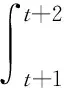

其中:M2是依赖k,v的正常数,T2是依赖k,v和R的正常数.
证明对方程(1.1)两边同时对x求导,然后两边同乘D7u,关于x于(0,1)上积分,得




+6(w2′(u)+w3′′(u))Du|D2u|2]D7udx

由Nirenberg不等式和Young不等式可得

同理,可得

由Young不等式和Hölder不等式可得

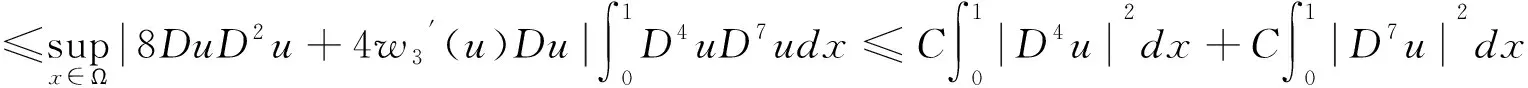
综上,有
由Gronwall不等式可知



其中:M3是依赖k,v的正常数,T3是依赖k,v和R的正常数.
证明对方程(1.1)两边作用拉普拉斯算子,然后两边同乘D8u,关于x于(0,1)上积分,得

+3w0′′(u)D2u+12w2′′′(u)(Du)4+(27w2′′(u)+12w3′′′(u))(Du)2D2u+(6w2′(u)+6w3′′(u))





由Nirenberg不等式和Young不等式,有

由Young不等式和Hölder不等式可得




综上所述,可以得到
由Gronwall不等式可得

由Sobolev嵌入定理,有||D4u||∞≤C25.
令v=ut,方程(1.1)两边作用拉普拉斯算子,然后两边同乘v,关于x于(0,1)上积分,得

+7||w2′′(u)(Du)3||∞+2||w3′′′(u)(Du)3||∞+6||w2′(u)DuD2u||∞+6||w3′′(u)DuD2u||∞)
||D2u||+(||w0′(u)||∞+3||w2′(u)(Du)2||∞+5||w3′′(u)(Du)2||∞+7||w3′(u)D2u||∞

从而,有
(2.7)
令t≥T3,取s∈(t,t+1),对上述不等式在(s,t+1)上积分,可得
||D4u(t+1)||2-||D3u(t+1)||2≤C25+||D4u(s)||2-||D3u(s)||2.
对上述不等式关于s于(t,t+1)上积分,有

(2.8)

由中值定理可知,存在时间t0′′∈(t+1,t+2), 有||Dv(t0′′)||2≤C28.引理2.4得证.

其中:M4是依赖k,v的正常数,T4是依赖k,v和R的正常数.

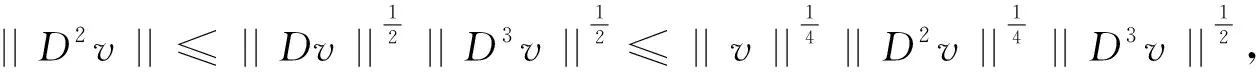
≤C[||D2v||2+(||w0′′′(u)(Du)2||∞+||w0′′(u)(D2u)||∞+||w2′′′(u)(Du)4||∞+||2w3′′′(u)(Du)2D2u||∞
+||3w2′′(u)(Du)2D2u||∞+||2w3′′(u)(D2u)2||∞+||3w3′′(u)DuD3u||∞+||w3′(u)D4u||∞)||v||2
+(||6D2uD3u||∞+||2DuD4u||∞+||2w0′′(u)Du||∞+||4w2′′(u)(Du)3||∞+||6w2′(u)DuD2u||∞
+||4w3′′(u)DuD2u||∞+||3w3′(u)D3u||∞)||Dv||||v||+( ||6(D2u)2||∞+||6DuD3u||∞
+||w0′(u)||∞+||3w2′(u)(Du)2||∞+||2w3′′(u)(Du)2||∞+||4w3′(u)D2u||∞)||D2v||||v||


令k充分大且满足C30k-C29>0,有
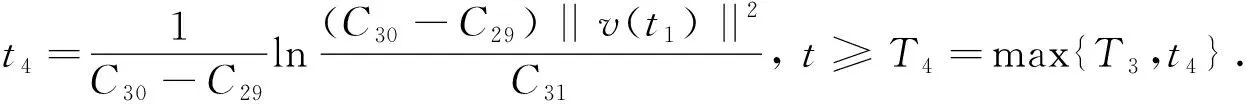

||Dut||≤M5,∀t≥T5,
其中:M5是依赖k,v的正常数,T5是依赖k,v和R的正常数.
证明由Nirenberg不等式,可知
令v=ut,方程(1.1)两边对t求导,然后等式两边同乘D2v,关于x于(0,1)上积分,得
=||D3v||2-([D2(|Du|2D2u)]t,D2v)+([D2(w0(u)+w2(u)(Du)2+w3(u)D2u)]t,D2v)
≤C[ ||D3v||2+(||w0′′′(u)(Du)2||∞+||w0′′(u)D2u||∞+||w2′′′(u)(Du)4||∞+||2w3′′′(u)(Du)2D2u||∞+||3w2′′(u)(Du)2D2u||∞+||2w3′′(u)(D2u)2||∞+||3w3′′(u)DuD3u||∞+||w3′(u)D4u||∞)
||v||||D2v||+(||6D2uD3u||∞+||2DuD4u||∞+||2w0′′(u)Du||∞+||4w2′′(u)(Du)3||∞
+||6w2′(u)DuD2u||∞+||4w3′′(u)DuD2u||∞+||3w3′(u)D3u||∞)||Dv||||D2v||
+(||6(D2u)2||∞+||6DuD3u||∞+||w0′(u)||∞+||3w2′(u)(Du)2||∞+||2w3′′(u)(Du)2||∞
+||4w3′(u)D2u||∞)||D2v||2+( ||6DuD2u||∞+||3w3′(u)Du||∞)||D3v||||D2v||

从而,可得
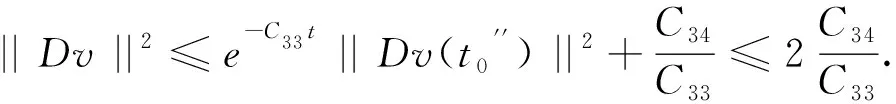


其中:M6是依赖k,v的正常数,T6是依赖k,v和R的正常数.
证明由原方程(1.1)可知
D6u=ut-D4u+2(D2u)3+6DuD2uD3u+(Du)2D4u-w0′′(u)(Du)2-w0′(u)D2u-w2′′(u)(Du)4-(3w2′(u)+2w3′′(u))|Du|2D2u-2w3′(u)|D2u|2-3w3′(u)DuD3u-w3(u)D4u.
由引理2.1-2.6,有



+||w3(u)||∞||D4u||
≤C34,对于任意的t≥T5.
从而引理2.7得证.
3 定理1.1的证明

假设M1和M6分别是引理2.2和引理2.7中的常数.然后表示为



D6u=v-D4u+D2[|Du|2D2u]-D2[w0(u)+w2(u)|Du|2+w3(u)D2u].

(3.1)
其中:M5和M6是正常数.当tn→∞时,存在N>0,使得对所有的n≥N都有tn≥T.因此,根据(3.1)得
(3.2)

(3.3)

然后由(3.1)和(3.3)得
||Dun(tn)-Du||→0,||D2un(tn)-D2u||→0,||D3un(tn)-D3u||→0, ||D4un(tn)-D4u||→0.我们还可得到:
||(D2un(tn))3-(D2u)3||
||Dun(tn)D2un(tn)D3un(tn)-DuD2uD3u||
≤C[ ||Dun(tn)D2un(tn)||∞||D3un(tn)-D3u||+||D3uDun(tn)||∞||D2un(tn)-D2u||+
||D2uD3u||∞||Dun(tn)-Du||] →0,
同理,有 ||(Dun(tn))2D4un(tn)-(Du)2D4u||→0,||(Dun(tn))2-(Du)2||→0,
||(Dun(tn))4-(Du)4||→0,||(Dun(tn))2D2un(tn)-(Du)2D2u||→0,
||(D2un(tn))2-(D2u)2||→0, ||Dun(tn)D3un(tn)-DuD3u||→0.
下面,我们给出定理1.1的证明.


