几乎超b-紧空间的若干性质研究

宋嘉丽，张国芳

（1.吉林师范大学 数学学院，吉林 长春 130000；2.吉林师范大学 数学学院，吉林 四平 136000）

0 引言

1983年，Mashhour等人在On superatopological spaces［1］去掉了拓扑空间中有限交的条件，给出了超拓扑空间的定义：2X的一个子集族μ叫做X上的超拓扑，如果满足下面两个条件：（1）X∈μ；（2）μ中元素的任意并仍在μ中.偶对( )X，μ称为超拓扑空间，μ中元素称为超开集，超开集的补集称为超闭集.2008年，Ab⁃bas［2］在On supra compactness in supra topologicol spaces中得出了超紧空间的超闭子集是超紧的，超紧空间在S*连续映射下的像是超紧的等结果.2010年，Sayed等［3］在On supra b-open sets and supra b-continuity on to⁃pological spaces中定义了超b-开集，在此定义的基础上定义了超b-连续映射，研究了超开集与超b-开集的关系，得出了关于超b开集和超b-连续映射的一些结果.2012年，Mustafa［4］在Totally supra b-continuous and slightly supra b-continuous function中利用超b-闭开集定义了超b-T1公理和超b-T2公理，得出了超b-T1公理和超b-T2公理在不同超b-连续映射下的性质.2013年，Mustafa［5］在supra b-compact and supra b-lindelöf spaces中给出了超b-紧空间和超b-lindelöf空间的概念，证得了超b-紧空间（超b-lindelöf空间）的超b-闭子集是超b-紧（超b-lindelöf）的，超b-紧子集的有限并是超b-紧的等相关性质.2016年，Al-shami［6］在some results related to supratopological space中给出了超lindelöf空间、几乎超紧（几乎超lindelöf）空间和弱超紧（弱超lindelöf）空间的概念，且研究了它们的性质，得出每个超紧（超lindelöf）空间是弱超紧（弱超lindelöf）空间等结果.2017年，Al-shami等［7］在Utilizing supra α-open sets to generate new types of supra compact and supra lindelöf spaces中给出了超α-紧空间、超α-lindelöf空间、几乎（弱）超α-紧空间和几乎（弱）超α-lindelöf空间的定义，得出了每个超α-紧空间都是超α-lindelöf空间等结果.在超紧空间和超b-紧空间中的性质研究已经比较完善，那么在它们的推广空间——几乎超b-紧空间和弱超b-紧空间的遗传性和映射性质是否成立呢？针对上述问题，本文探究了它们的遗传性和映射性质.

1 预备知识

定义1［3］称A是(X，μ)中的超b-开集，在超拓扑空间(X，μ)中，若满足A⊆clμ(Intμ(A))⋃Int(clμ(A)).超b-开集的补集是超b-闭集；超b-闭集的补集是超b-开集.

定义2［3］称clbμ(A)为A的超b-闭包，如果满足clbμ(A)是包含A的所有超b-闭集的交.

定义3［3］称{Ai：i∈I} 是X子集B的超b-开覆盖，设{Ai：i∈I} 是超拓扑空间(X，μ)的超b-开子集族，如果满足B⊆⋃{Ai：i∈I}.

定义4［2］称超空间X是超紧空间，如果对于X的任意超开覆盖μ都存在一个有限超子覆盖.

定义5［6］称(A，τA)是(X，τ)的超子空间，如果满足A⊆X，τA=A⋂B(B∈τ).

定义6称超空间X是几乎超b-紧空间（几乎超b-lindelöf空间），如果对于X的任意超b-开覆盖μ都存在一个有限（可数）子族ℓ，满足{clbμ(V)|V∈ℓ} 覆盖X.

定义7称超空间X是弱超b-紧空间（弱超b-lindelöf空间），如果对于X的任意超b-闭开覆盖都存在一个有限（可数）的超子覆盖.

定义8称f为超b∗连续映射：设(X，μ)，(Y，σ)是两个拓扑空间，μ∗和σ∗分别是μ和σ的伴随超拓扑，映射f：(X，μ)→(Y，σ)，如果对于Y中每个超开集V，满足f-1(V)是X中的超b-开集.

2 主要结果

Mustafa在文献［5］中给出了X为超b-紧空间（超b-lindelöf空间）的定义：如果对于X的任意超b-开覆盖μ都存在一个有限（可数）超子覆盖.

定理1任意的超b-紧空间必为几乎超b-紧空间.

证明：令X是超b-紧空间，则对于X的任意超b-开覆盖{Gi：i∈I} 都存在一个有限的超子覆盖{G1，G2，…，Gn} ，即由于任意超b-开集都包含在它的超b-闭包中，所以，故X的 任 意 超b- 开 覆 盖{Gi：i∈I} 均 存 在 一 个 有 限 子 族覆盖X.故X是几乎超b-紧空间.类似可证超b-lindelöf空间一定是几乎超b-lindelöf空间.

上述命题的反命题不成立，下面的例子说明几乎超b-lindelöf空间未必是超b-lindelöf空间.

Mustafa在文献［5］中得出了几乎超b-紧空间都是几乎超b-lindelöf空间的结论.

例1设μ={φ，G⊆R，st0 ∈G} 是R上的超拓扑.因为，所以(R，μ)是几乎超b-紧空间，从而(R，μ)是几乎超b-lindelöf空间.另一方面，设ℓ={{ 0，x} ：x∈R} 是R中的超b-开集族，显然是R的超b-开覆盖.显然ℓ={{ 0，x} ：x∈R} 不存在可数的超子覆盖，故(R，μ)不是超b-lindelöf空间.

定理2几乎超b-紧空间的超b-闭子集是几乎超b-紧的.

证明：设F是几乎超b-紧空间(X，μ)的一个超b-闭子集，并且{Gi：i∈I} 是由X中超b-开集构成F的超b-开覆盖，即F⊆⋃{Gi：i∈I}.因为F是超b-闭集，所以补集Fc是超b-开集.从而( ⋃{Gi：i∈I})⋃Fc是X的一个超b-开覆盖.因为X是几乎超b-紧空间，所以存在有限的子族：

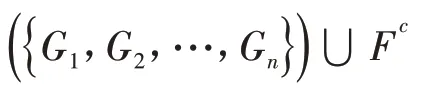
Mustafa在文献［4］中给出了超b-闭开集的定义：A是超b-闭集也是超b-开集.超b-闭开集的补集是超b-满 足闭开集.

定理3如果A是X的一个几乎超b-紧子集，B是X的一个超b-闭开集，则A⋂B是几乎超b-紧的.

证明：设ℓ={Gi：i∈I} 是A⋂B的一个超b-开覆盖.因为B是超b-闭开集，所以B的补集Bc也是超b-闭开集.从 而{Gi：i∈I} ⋃{Bc} 是A的 一 个 超b-开 覆 盖.因 为A是 几 乎 超b-紧 的，所 以A的 超b-开 覆 盖{Gi：i∈I} ⋃{Bc} 存在有限子族{G1，G2，…，Gn} ⋃{Bc} ，并且满足覆盖A，从 而{G1，G2，…，Gn} 是A⋂B的 超b- 开 覆 盖ℓ={Gi：i∈I} 的 有 限 子 族 ，并 且 满 足覆盖A⋂B.故是A⋂B是几乎超b-紧的.

Al-shami文献［7］中给出了X是几乎超紧空间（几乎超lindelöf空间）的定义：如果对于X的任意超开覆盖μ都存在一个有限（可数）子族ν，满足{clμ(V)|V∈ν} 覆盖X.

定理4设f：(X，μ)→(Y，σ)是超b∗连续映射，并且是满射.如果X是几乎超b-紧空间，则Y是几乎超紧空间.

证明：设f：(X，μ)→(Y，σ)是从几乎超b-紧空间(X，μ)到超拓扑空间(Y，σ)上的超b∗连续映射，且ℓ={Ai：i∈I} 是(Y，σ)的一个超开覆盖.因为f是超b∗连续映射，所以{f-1(A i)：i∈I} 是(X，μ)的超b-开覆盖.由于(X，μ)是几乎超b-紧空间，则超b-开覆盖{f-1(A i)：i∈I} 存在有限子族{f-1(A1)，f-1(A2)，…，f-1(A n)}，满足

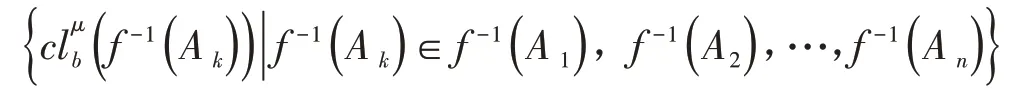
覆盖X.即因为f是满射，所以f(X)=故Y是几乎超紧空间.

定理5任意的几乎超b-紧空间都是弱超b-紧空间.

证明：设(X，μ)是几乎超b-紧空间，且ℓ={Hi：i∈I} 是(X，μ)的超b-闭开覆盖.因为(X，μ)是几乎超b-紧的，所以ℓ={Hi：i∈I} 存在着有限子族{H1，H2，…，Hn} ，并且满足{clbμ(H)|H∈{H1，H2，…，Hn} }覆盖X.因为Hi是超b-闭开集，所，因此{H1，H2，…，Hn}是(X，μ)的超b-闭开覆盖ℓ={Hi：i∈I} 的有限超子覆盖，故X是弱超b-紧空间.

定理6任意的弱超b-紧空间中的超b-闭开集是弱超b-紧的.

证明：设F是弱超b-紧空间X中的一个超b-闭开集，并且{Gi：i∈I} 是F的一个超b-闭开覆盖.因为F是超b-闭开集，所以Fc是超b-闭开集.从而{Gi：i∈I} ⋃{Fc} 是X的一个超b-闭开覆盖.因为X是弱超b-紧空间，所以X的一个超b-闭开覆盖{Gi：i∈I} ⋃{Fc} 存在有限超子覆盖{G1，G2，…，Gn} ⋃{Fc} ，从而{G1，G2，…，Gn} 是F的超b-闭开覆盖{Gi：i∈I} 的有限超子覆盖，故是F弱超b-紧的.

Sayed等人在文献［3］中给出了f为超b-连续映射的定义：设(X，μ)，(Y，σ)是两个拓扑空间，μ∗是μ的伴随超拓扑，映射f：(X，μ)→(Y，σ)，如果对于Y中每个开集V，满足f-1(V)是X中的超b-开集.

定理7弱超b-紧子集在是超b-连续映射下的像是紧的.

证明：设(X，μ)是超拓扑空间，A⊆X，f：X→Y是超b-连续映射，且{Ai：i∈I} 是f(A)的一个开覆盖，即因为f是超b-连续映射，所以是A的超b-开覆盖.由于A是超b-紧子集，故存在有限超子覆盖，设为为f(A)的开覆盖{Ai：i∈I} 的有限子覆盖，故f(A)是紧的.

3 结语

本文在超紧空间和超b-紧空间中的性质基础上，研究了它们的推广空间—几乎超b-紧空间和弱超b-紧空间的遗传性和映射性质，得出以下结论：几乎超b-紧空间中的超b-闭子集是几乎超b-紧的，弱超b-紧空间中的超b-闭开子集是弱超b-紧的，几乎超b-紧空间在超b∗连续满射下的像是几乎超紧的，并给出了详细的证明.在超可数紧空间和超b-可数紧空间的基本性质的基础上，几乎超b-可数紧空间的性质研究有待于进一步的完善.本文的研究拓展了超紧空间和超b-紧空间的研究领域，为其他类型的超紧空间的研究提供了理论思想和研究方法.