深度学习视角下初中数学微专题教学的实践与反思

周玉俊 赵军

【摘 要】“微专题”本质上是一种以学习“四基”、发展“四能”、提升学科素养为指向的学材重构方式，和集灵活性、创新性于一体的教学组织形式。“微专题”的实施应坚持以生为本，突出主体性;坚持因需而教，注重灵活性;坚持实践创新，体现适切性。

【关键词】深度学习;微专题;主体性;灵活性;适切性

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2021）80-0034-04

【作者简介】1.周玉俊，江苏省东台市教师发展中心（江苏东台，224200）教研员，高级教师;2.赵军，江苏省太仓市实验中学（江苏太仓，215400）教师，正高级教师，江苏省特级教师。

传统的单元教学，无论是新授课还是复习课，往往局限于某个单元，缺少知识的前后联系和对教学内容的关联重组，教师在教学中也往往忽视学生的主动参与和对知识的深度理解。在教学中充分调动学生的主动性，激发其学习兴趣，培养良好的思维习惯和思维品质，需要教师更新教学理念，创新教学方法，重视学材重组和教学形式的变化。

近年来，笔者对“微专题”教学进行了一些尝试和探索，发现它是一种有效的学材重构方式和教学组织形式，可以激发学生学习的内在动力、提高学习效率，帮助学生加深对知识的理解，提升思维能力，培育核心素养。本文拟结合具体的教学案例，谈谈对“微专题”内涵价值的理解以及对教学实践的一些思考。

一、对“微专题”内涵的理解

受书面形式的制约，教材的编写往往具有一定局限性，教材固定的、规范化的形式限制了学科知识中隐含的丰富的思维过程的表达。“微专题”的开发和实施正是为了克服教材的这一局限性，力图通过学材重构和深度教学，实现从教材“冰冷的说理”到教学“火热的思考”的转化与融合。

微专题本质上是一种以学习“四基”、发展“四能”、提升学科素养为指向的学材重构方式，和集灵活性、创新性于一体的教学组织形式。微专题通常是在教授新课或单元复习过程中，围绕一个或几个紧密相关的知识或思想方法，形成一个专题研究。微专题也可以理解为针对某个特定目标，结合具体学情设计的、能够在短时间内解决的“问题集”， 这些问题集以知识和题型为载体，注重知识的前后联系和方法之间的本质关联，注重思想方法的引领和解题经验的积累，往往具有因“微”而专、因“微”而深、见微知著的特点。

二、“微专题”的教学价值

微专题教学以“立德树人”为核心价值，以知识深度加工、思维深度发展、意义深度建构为价值追求，以理解、应用、综合、评价、创造等高阶认知活动为主要学习形式，追求深度教学和深度学习。微专题的教学价值主要表现在以下三个方面。

1.有利于激发学生的学习动力，促进积极的情感体验。

相对于日常的新授课和复习课，微专题教学基于具体学情，立足学生学习的“最近发展区”，设计方法和教学形式灵活多样。知识的关联、教法的选用既重视学生的学科知识基础，更关注学生生命成长，重视学法指导，充分激发学生学习的内驱力，为深度学习创造和谐乐学的良好氛围。

2.有利于提高学生的学习效率，发展“四基”、培养“四能”。

微专题通常以课本上的典型例題、习题为载体，以“一题一课”“ 一图一课”“一法一课”等形式展开教学，注重关联前后的数学知识和解题方法，力求将零散的知识技能、数学思想和活动经验串联成线，使学生能够举一反三、触类旁通。微专题教学以“问题链”为主要教学形式，注重培养学生发现问题、提出问题、分析问题和解决问题的能力，最大程度提高学生的学习效率，减轻学习负担。

3.有利于促进学生的深度学习，提升学科核心素养。

微专题的实施以认知心理学原理、主体教育论、建构主义理论为指导，立足学生的认知基础，着力解决学生学习中的重点和难点问题，教学实施采用“题组+变式”的方式，促进学生主动学习、深度学习，注重培养学生的学习力和思维力，发展学生的创新意识和探究能力，提升学科核心素养。

三、 “微专题”教学案例：《“圆”来如此》

1.追根溯源，“一中同长”。

引例：苏科版九年级数学上册第38页，圆的集合定义。

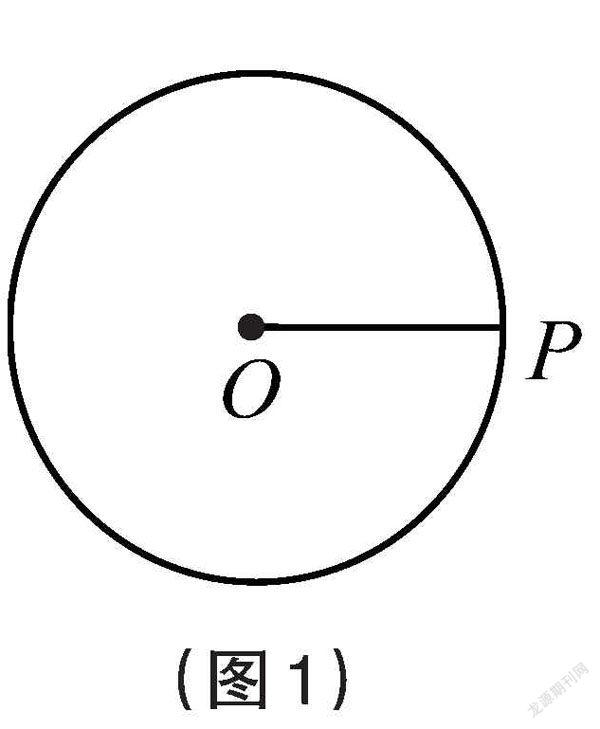
师：如图1，通过操作、观察可以发现，圆是由怎样的点形成的集合？

生：圆是到定点（圆心O）的距离等于定长（半径OP）的点的集合。

【教学意图】通过复习圆的集合定义，引导学生体会“一中同长”的含义，为后续解题过程中添加辅助圆解决问题打下理论基础。

2.变换载体，灵活运用。

探究1：“圆”来如此求角度

问题1：如图2，四边形ABCD中，BC=DC=AC，∠ACB=68°，∠ADB= _______ 。

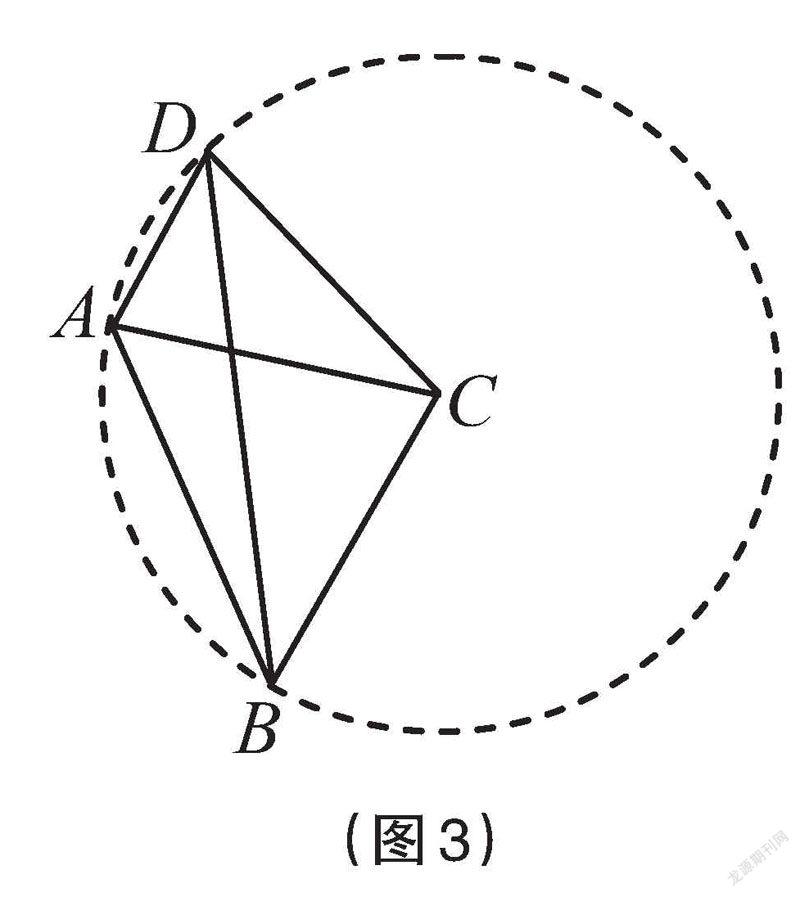
师：由条件BC=DC=AC可得哪几点共圆？

生：BC=DC=AC可以理解为B、D、A三个点到点C的距离相等，如图3，以点C为圆心、BC长为半径画圆，则点B、D、A都在这个圆上。

师：此时如何求∠ADB的度数？

生：此时∠ADB与∠ACB的关系实质上就是弧AB所对的圆周角与圆心角之间的关系，由此可以求出∠ADB的度数。

【教学意图】由引例中圆的“一中同长”特点，让隐形的圆显现，使学生经历“从无圆到有圆”的思考过程，体会找到图形中隐藏的圆之后解题的方便与快捷。

探究2：“圆”来如此求最值

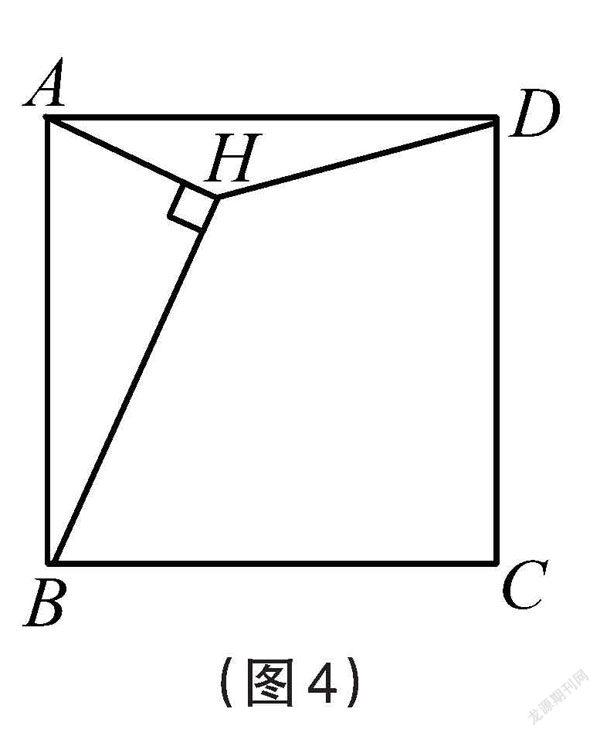
问题2：如图4，H是正方形ABCD内的一点，且AH⊥BH，连接DH，若正方形的边长为<f：＼教育8本书＼江苏教育2021＼江苏教育11期＼中学11期＼中学11期图片＼（周玉俊）深度学习视角下初中数学微专题教学的实践与反思-4DF8＼image27.pdf>，则线段DH长度的最小值是   。

师：由点H是动点，且AH⊥BH，你能想到什么？

生：点H到AB中点的距离保持不变，始终等于斜边AB的一半。

师：结合圆的集合定义，点H在什么图形上运动？

生：点H在正方形内部，且在以AB为直径的半圆上运动。

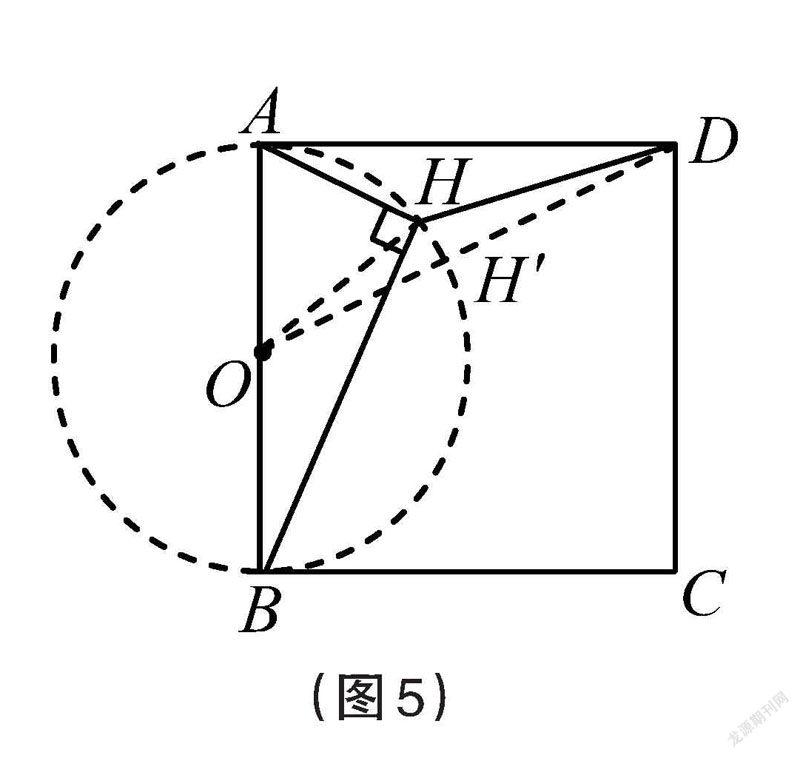
师（追问）：如何求DH的最小值？

生：如图5，可以看为⊙O外一点D到圆上的最短距离。

【教学意图】引导学生审题，明确点H到AB中点的距离保持不变，从而联想到点H的运动轨迹是一段圆弧，将问题转化为“圆外一点到圆上点的最小距离”，达到“化动为静、建构模型”的目的。

探究3：“圆”来如此求表达式

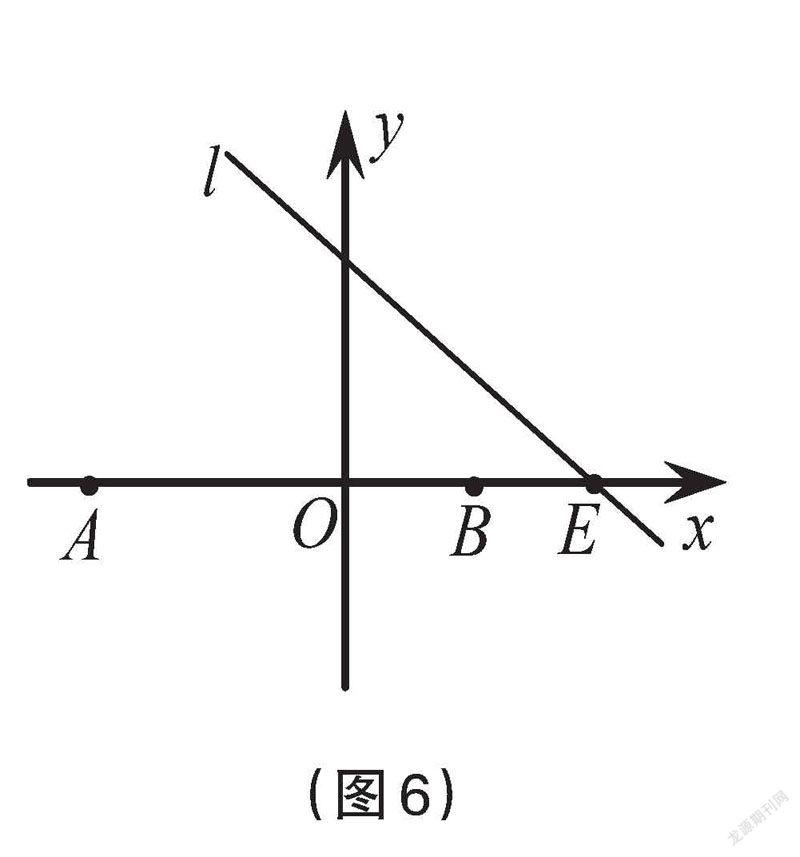
问题3：如图6，在平面直角坐标系中，点A（-4，0），点B（2，0）。若直线l过点E（4，0），M为直线l上的动点，当△ABM是以点M为直角顶点的直角三角形时，求直线l的表达式。

師：如何确定点M的位置？

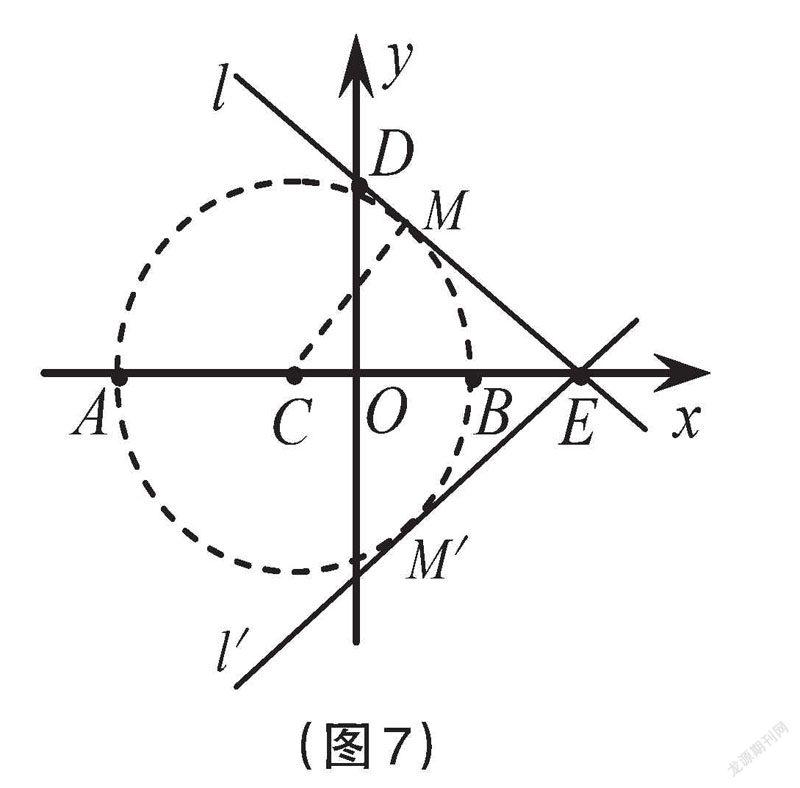
生：如图7，根据圆的集合定义，以AB为直径作⊙C，点M一定在这个圆上。

生（补充）：因为M为直线l上的动点，所以当直线l与⊙C相切时，切点即为点M。

师（追问）：这样的点有几个？如何求此时直线l的解析式？

生：两个，问题的关键是求D点坐标，可借助△CEM≌△DEO，求得OD=MC=3。

【教学意图】教师在引导学生分析出点M运动的轨迹后，将隐性的圆显性化，再利用圆的性质确定直线l的位置，彰显“‘圆’来如此”的魅力。

3.归纳小结，“圆”来如此。

师：回顾本节课所解决的问题，我们会发现始终有一个“隐形的圆”贯穿“题”中，归纳一下，什么情况下我们可以通过构造圆来解决问题？

生：在“有几条线段共端点且等长”或者“直角顶点在运动”的情况下可以通过构造圆来解决问题。

【教学意图】通过归纳小结，让学生重新审视“添圆法”的巧妙之处，加深对构造辅助圆的条件的理解，完善方法体系，构建“多题一法”，实现因“微”而专、见微知著的目的。

四、教学思考

微专题应当基于教情、立足学情，根据具体的教学内容灵活设计并实施。在教学过程中要突出以生为本，因情施教、按需施教，例题应根据学情选用。以此类推，微专题教学应遵循“从实践中来，到实践中去”的指导思想，坚持“开发—实践—修正—再实践—再修正”的实施路径，增强教学的有效性和针对性。

1.坚持以生为本，突出主体性。

主体性是微专题设计和实施的首要原则。微专题的设计要面向全体学生，从具体学情出发，把握好低起点、快反馈、多层次、富挑战、重实效的要求，体现基础性、层次性和综合性的特点。上述课例中对“添圆法”的教学设计就体现了这样的特点：首先，《“圆”来如此》这个标题足够吸引学生，蕴含着“添加了圆之后不过如此”，有化难为易之意;其次，对题目的安排由易到难、由浅入深，问题设置富有启发性。所以，微专题教学必须始终坚持以学定教、因材施教、学为中心、以教促学。

2.坚持因需而教，注重灵活性。

灵活性是微专题设计和实施的一个重要特征。微专题的设计方式灵活多样，可以是对某个知识板块的专题复习，也可以是对某些数学模型的变式探究，还可以是对某种数学方法（如旋转法、分析法等）进行指导的专题，抑或是某种“数学思想”（如化归、分类等）体悟的专题等，设计内容和上课形式不拘一格、灵活机动，教学实施注重相机而教、灵动生成。上述课属于“多题一法”，结合学情，我们还可以从“一题多法”、逆向编题等方面展开微专题的开发与实践。

3.坚持实践创新，体现适切性。

适切性是微专题设计和实施的质量保证。微专题教学的目的在于以教学设计为载体，帮助学生发展思维、提升素养，实现高效、高质、深度的学习。微专题教学的有效性要通过教学实践加以检验，注重校正优化以及再实施再优化的过程。上述课例在实际教学时一定要根据学情对题目进行增减，以让学生“跳一跳够得着”为标准，一切从实际出发，不能一味贪多求深。

在微专题教学的实施过程中，每一个专题都要尽量做到“小开口，大方法”。在选题上力求以小见大、微中见法，将某一方法、思想、技巧、模型深入剖析、归纳提炼，形成一系列互相独立而又相互关联的微专题案例。在具体的实施过程中，需要着眼于学生的思维发展、能力提升和数学素养的形成，将微专题的开发、实践与深度教学、深度学习相结合，与学生创新精神和实践能力的培养相结合，有效地提升学生的综合素质。

【参考文献】

[1]郭华.深度学习及其意义[J].课程·教材·教法，2016（11）：25-32.

[2]余文森.核心素养导向的课堂教学[M].上海：上海教育出版社，2017.

本文系江苏省教育科学“十三五”规划2020年度课题“探索与重构：数学发现真正的教学路径研究”（E-c/2020/31）的研究成果。

3853500589239