面向复杂障碍场的多智能体系统集群避障模型

张超省， 王健， 张林， 王娅

(1.陆军工程大学 训练基地， 江苏 徐州 221004； 2.空军勤务学院 基础部， 江苏 徐州 221200)

0 引言

随着导航技术、通信技术、控制技术和人工智能技术的发展，未来会有越来越多的无人机、无人车、无人艇等无人装备走向战场，担负侦察、警戒、核生化检测、弹药补给、人员抢救、装备抢修等任务，甚至是成为主战装备中的一员。由多个无人装备组成的多智能体系统，可以替代战士执行作战任务，最大限度地减少人员伤亡[1]。对于投入战场的多智能体系统而言，既要能够充分发挥集群的规模效应，避免过多个体游离群体之外，还要能够在尽量保持集群的前提下快速地穿越复杂障碍场。尤其是在地面战场上，多智能体系统不仅仅要面临阻绝墙、铁丝网、三角锥、堑壕等传统的障碍体，还需要绕过路径上的掩体工事、武器装备等形成的阻挡。因此集群避障技术是提高多智能体群体地面战场适应能力的关键。

对集群行为的研究起源于Reynolds等[2]对鸟群行为的计算模拟，提出群中个体应遵循的3条基本规则，即避免碰撞、速度匹配和保持聚集。在Reynolds等的基础上，Toner等[3]、Couzin等[4]和Vicsek等[5]先后开展了一系列卓有成效的研究工作，形成了3个经典的群集动力学模型，但这些工作均是在自由空间内对集群行为的模拟。

在智能体避障规则方面，有以下具有代表性的研究成果。2004年，Tanner等[6]基于车辆周围的球面邻域中获得的局部信息，提出了一系列非光滑控制律，使车辆能够在静态障碍物中集群达到目的地。2010年，Wang等[7]从逆最优控制的角度出发，构造了一个非二次罚函数来实现集群的避障能力，并证明了一致算法的渐近稳定性和最优性。2010年，Yan等[8]针对多智能体系统中的目标跟踪和避障问题，提出了一种基于人工势函数和行为规则的控制算法，解决了动态环境下集群避障时无法有效跟踪目标的问题。2012年，Bai等[9]提出了一种将流量函数与人工势场相结合的新框架，定义了一种具有可见性约束和层次关联的动态结构以提高系统的性能。2015年，Burohman等[10]采用输入输出线性化方法控制集群避障，提出了一种非完整移动机器人的群集算法，实现了狭窄通道的无碰撞通行。

在障碍体几何模型方面，有以下具有代表性的研究成果。2006年，Olfati-Saber[11]通过引入两种虚拟智能体(β-智能体和γ-智能体)来表示障碍体和目标对智能体集群的作用，实现了多个障碍条件下的集群避障问题，成为集群避障领域的经典模型；然而，该模型只用直线和外接圆模拟障碍体，不能模拟复杂的障碍体形状。2011年，Ghorbanian等[12]把环境中的障碍物用椭圆形状逼近和封闭，设计了分布式控制规则来实现多智能体群体避障运动。2012年，Hu等[13]采用圆锥形结构模拟运动场中的三维障碍物，并引导智能体沿着锥面上最短的路径通过障碍物。2017年，Qiu等[14]采用临时目标法，实现了多智能体在规则直角障碍体中的集群避障。

为便于研究，将地面战场近似为二维平面，那么地面战场上无人装备集群躲避多个障碍体的问题便可以抽象为二维空间内多智能体系统集群穿越复杂障碍场的问题。假设一组智能体集群从某地出发到目的地执行任务，必经之路上存在一个由若干障碍体组成的复杂障碍场，如图1所示，障碍区域中黑色多边形表示障碍体原本的形状，灰色圆形表示障碍体的最小外接圆。由图1可以看出：障碍体之间原本存在比较大的间隙，能够作为智能体集群的通道。然而，传统人工势场法多采用障碍体的最小外接圆(球)作为多边形障碍体的边界，那么原本存在的通道将变窄甚至消失。为了解决上述问题，本文设计了一套面向复杂障碍场的智能体集群避障模型及求解方法。

图1 面向复杂障碍场的多智能体系统集群Fig.1 Flocking of multi-agent system in complex obstacle field

1 集群避障运动的建模

为了更清楚地阐述集群避障运动的建模过程，引入σ-范数、隆起函数、集群避障运动控制方程等概念。

为了确保向量z的范数‖z‖处处可微分，定义向量z的σ-范数为

(1)

式中：ε∈(0,1]。

为了构建平滑势函数，采用如(2)式所示的隆起函数：

(2)

式中：h为控制隆起位置的参数，h∈(0,1)。

基于Olfati-Saber的算法3[11]，改进多边形障碍体环境下的集群避障控制方程，采用(3)式计算第i个智能体的运动：

(3)

1.1 其他智能体对智能体Ai的作用

将多智能体系统视作一个由M个智能体组成的集合V，为便于表示，第i个智能体Ai的外接圆记为B(CAi,RAi)，其中，CAi、RAi分别表示智能体Ai的外接圆圆心(外心)和外接圆半径(外径)。

多智能体系统进行集群运动，智能体Ai的运动状态为

(4)

式中：qi、pi、ui分别为智能体Ai的位置、速度和加速度，qi,pi,ui∈RD，D表示维度。为简化分析，可以用智能体Ai外心位置CAi作为智能体Ai的位置。

由于智能体必然为实体，存在一定的体积。定义智能体Ai边界与智能体Aj边界的距离为

d(Ai,Aj)=‖CAi-CAj‖-RAi-RAj，

(5)

式中：‖·‖表示多维空间的欧几里得范数。

当智能体之间距离过大时，智能体之间相互影响忽略不计，定义智能体Ai邻居的集合为

(6)

图2给出了某个时刻智能体Ai周围智能体的分布，浅色阴影圆形(虚线)表示智能体Ai的交互距离，深色阴影圆形(实线)表示智能体Ai的外接圆。根据(6)式，可以看出：智能体A1、A2、A5都是智能体Ai的邻居，而智能体A3、A4都不是智能体Ai的邻居。

图2 智能体Ai的邻域空间Fig.2 Neighborhood space of agent Ai

基于冲击函数(2)式，定义智能体之间的空间邻接矩阵A(q)=[aij(q)]，其中元素为

(7)

定义智能体之间的功能函数为

(8)

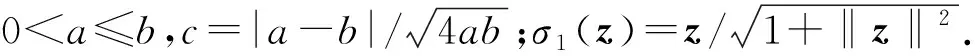
智能体Ai的邻居对其作用的方程为

(9)

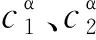
(10)

1.2 障碍体对智能体Ai的作用

图3 障碍体Ok对智能体Ai的作用Fig.3 Interaction between agent Ai and obstacle Ok

步骤1智能体Ai外接圆边界与多边形障碍体Ok外接圆边界之间的距离，通过(11)式求解：

(11)

步骤2多边形障碍体Ok相对于智能体Ai是否激活，定义智能体Ai附近所有激活障碍体的集合为

(12)

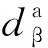
(13)

(14)

P1PC·PCP2≥0，

(15)

步骤5假设激活边为P1P2，进一步求解智能体Ai外心CAi与障碍体Ok的激活边P1P2的垂线，垂足为K，连线CAiK通过(16)式求出：

(16)

式中：CAiP1为智能体Ai外心到障碍体顶点P1之间的连线(矢量)；Δ为连线CAiP1与连线P1P2之间的夹角θ的余弦值，可由(17)式求出：

(17)

步骤6多边形障碍体Ok相对于智能体Ai是否排斥，通过(18)式判定：

(18)

步骤7当智能体Ai处于障碍体Ok的排斥距离内，引入一种虚拟智能体来模拟障碍体对智能体的作用，并将这种虚拟智能体记为β-智能体。β-智能体的位置即为智能体Ai在障碍体Ok边界上的直角投影(正投影)，β-智能体的位置和速度由(19)式可得：

ik=K，ik=Ppi，

(19)

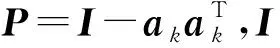
(20)

步骤8基于冲击函数(2)式，定义智能体Ai与障碍体Ok之间的空间邻接矩阵B(q)=[bik(q)]，其中元素为

(21)

步骤9智能体Ai与障碍体Ok之间的作用函数为

(22)

步骤10智能体Ai临近障碍体对智能体Ai的作用方程为

(23)

(24)

1.3 目标对智能体的作用

智能体的目标可以是静态的，也可以是动态的，因此目标Gγ可定义为

Gγ=(qγ，pγ)，

(25)

式中：qγ、pγ分别表示目标的位置和速度，当pγ=0时，目标静止不动。

基于人工势能函数，目标对于智能体Ai的引领作用可由(26)式直接给出：

(26)

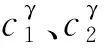
2 集群避障运动的求解

通过采用多边形表示障碍体，能够解决传统人工势场方法采用最小外接圆(球)表示障碍体造成的通道变窄和堵塞问题。然而，多边形的直边可能会引起捕获现象[11]，如何逃离直边捕获是智能体集群避障模型必须要解决的另一个重要问题。

2.1 直边捕获问题

图4 障碍体Ok直线边P1P2对智能体Ai的捕获现象Fig.4 Capturing phenomenon of edge P1P2 of obstacle Ok to agent Ai

1)求解智能体Ai外心CAi与目标Gγ的连线CAiGγ与障碍体Ok排斥边P1P2的交点，参考(13)式，如果该交点同时位于线段CAiGγ和障碍体Ok排斥边P1P2上，则该排斥边为捕获边；

2)求解智能体Ai外心CAi与障碍体Ok排斥边端点的距离，以排斥边为P1P2为例，通过(27)式判定：

(27)

如果(27)式成立，则该排斥边为捕获边。

如果排斥边为捕获边，则将目标设置为临时目标。临时目标根据智能体Ai、捕获边端点P1P2、目标Gγ三者的位置确定，由智能体位置向排斥边作垂线，当垂足K位于排斥边之内时，临时目标点通过(28)式求解：

(28)

式中：Ln为连线P1P2的法向量；Pn=P1P2/‖P1P2‖；Π=(‖CAiP1‖+‖P1Gγ‖)-(‖CAiP2‖+‖P2Gγ‖)。

当垂足K位于排斥边之外时，临时目标点通过(29)式求解：

(29)

如果只考虑障碍物静止的情况，此时：

(30)

2.2 离散化求解方法

(4)式为位置、速度和加速度的数学关系，以连续导数的形式给出。仿真过程中，往往需要离散形式。因此，需要修改(4)式的形式，具体作法为：

1)通过(3)式可以获得智能体Ai某时刻的加速度ui，实际上智能体加速能力不可能无限大，设智能体驱动加速度最大值为umax，则应作出以下判定：

‖ui‖>umax.

(31)

当(31)式成立时，说明计算获得的加速度大于智能体最大加速度，则令

ui=umaxui/‖ui‖，

(32)

否则，不作改变。

2)通过(33)式计算智能体Ai某时刻的速度：

pi=p′i+u′iδt，

(33)

式中：δt为离散时间步长；p′i、u′i分别为智能体Ai在前一个时刻的速度和加速度。

同样，智能体速度不可能无限大，设智能体速度最大值为pmax，则首先作出如(34)式判定：

‖pi‖>pmax.

(34)

当(34)式成立时，说明计算获得的速度大于智能体最大速度，则令

pi=pmaxpi/‖pi‖,

(35)

否则，不作处理。

3)通过(36)式计算智能体Ai某时刻位置：

(36)

式中：q′i为智能体Ai在前一个时刻的位置。

2.3 关键参数选取规则

关键参数选取规则为：

(37)

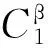
(38)

3)智能体之间、障碍体与智能体之间、目标点与智能体之间的速度影响因子与距离影响因子大致满足：

(39)

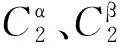
在该规则指导下，本文所提出的集群避障模型能够完成集群避障要求，但由于离散化求解方法和多智能体系统固有的不确定性，构形必然会暂时遭到破坏，因此上述规则仅能保证尽可能大的构形保持率。

(40)

(41)

3 仿真验证

以某时刻智能体Ai为对象，上述集群避障运动建模和求解过程可以通过图5所示的流程图进行。首先，根据智能体和障碍体的几何属性完成参数初始化，顶层虚线框所示；其次，分别计算其他智能体、障碍体和目标点对智能体Ai的作用，中间层从左至右虚线框所示；最后，综合所有作用力，离散化计算智能体的加速度、速度和位移，底层虚线框所示。

图5 集群避障建模及求解流程图Fig.5 Flow chart of flocking model and its solution

下面给出20个智能体穿越障碍场、抵达目标的仿真结果。初始时刻，该组智能体外接圆半径均为1.0 m，以[25 m,0 m]为起始位置、以4×5的阵型和2 m的间隔、沿x轴正向并关于x轴对称分布，所有智能体的初始速度均为[0 m/s，0 m/s]。

复杂障碍场由2个三角形、2个四边形和1个五边形障碍体组成，其顶点坐标位置可以表示为

F={[130 m,30 m;150 m,50 m；160 m,0 m]，
[80 m，-60 m;110 m，-50 m;90 m，-30 m]，
[130 m，-50 m;120 m，10 m;150 m，0 m;160 m，-25 m]，
[90 m，-20 m;92 m，-21 m;94 m，21 m;89 m，20 m]，
[90 m，40 m;110 m，20 m;130 m，40 m;
120 m，55 m;100 m，55 m]}，

其中，每一行表示一个障碍体的顶点坐标(x，y)，各顶点以分号隔开，各障碍体均静止不动。模型中的参数如表1所示。

表1 模型参数

图6 静态目标下多智能体系统集群避障Fig.6 Obstacle avoidance of multi-agent system when moving in the direction of static target

第1个任务是集群穿越障碍场，达到静态目标周边。目标状态由Gγ=(qγ,pγ)确定，其中qγ=[220 m， 0 m]，pγ=[0 m/s， 0 m/s]。第1个任务对应的集群运动过程如图6所示，其中黑色多边形表示障碍体，红色圆形表示智能体，红色五角星表示目标。为了更好地展示智能体集群在遇到障碍物时的分离与集合行为，坐标范围经过人为设定。由图6可以看出：初始时，智能体相对密集地集中于出发点，如图6(a)所示；随后，智能体之间保持期望距离并抵达条形障碍体附近，如图6(b)所示；当智能体进入条形障碍体的排斥距离时，由于(28)式和(29)式的作用，智能体分别选择了两个不同的临时目标，开始分裂为两组集群，如图6(c)所示；下面一组智能体集群继续分裂成两组智能体集群通过四边形障碍体，如图6(d)所示；当多数智能体通过后侧三角形和四边形障碍体之间时，由于通道较窄，出现非常明显的挤压行为，智能体只能鱼贯而出，如图6(e)所示。通过图6还可以看到：在避障时，有少数智能体没有与大多数智能体组成的集群连结，然而，当通过障碍体后，智能体都以相同速度朝目标方向运动迅速形成集群，如图6(f)、图6(g)和图6(h)所示。

第2个任务是集群穿越障碍场，智能体集群分成两组实现两个动态目标追踪或攻击。两个目标的状态为

其中：A表示幅值，A=20 m；ω为角速度，ω=0.01π rad/s.

图7 动态目标下智能体集群避障Fig.7 Obstacle avoidance of multi-agent system when moving in the direction of dynamic target

在其他参数保持不变的条件下，第2个任务对应的集群运动过程，如图7所示，其中红色圆形和红色星标分别表示第1组智能体及其对应目标，蓝色圆形和蓝色星标分别表示第2组智能体及对应目标。由图7可以看出：刚开始时，所有智能体以一个集群以特定构形到达障碍场附近，如图7(a)所示；随后，由于障碍体的排斥作用，集群开始分离，构形遭到破坏，如图7(b)所示；由于目标牵引作用，当大部分智能体越过障碍场后又开始逐步形成新的集群，并分别朝着各自对应的目标集群运动，如图7(c)和图7(d)所示；当两个目标交汇时，两组智能体集合在一起，如图7(e)所示；当两个目标重新分离时，两组智能体朝向各自的目标离散，如图7(f)所示；当两个目标再次靠近又分离时，两组智能体再次集合之后又朝着各自的目标离散。此处存在个别(红色)智能体被胁迫到另一组(蓝色)智能体集群中，如图7(d)、图7(f)和图7(h)所示。不难得出结论：在两个动态目标存在下，模型依然能够对发挥较好的支配作用。但是，两组智能体离散时存在的胁迫现象还需要设计其他规则加以消除，比如不同目标对应智能体之间只存在排斥力不存在吸引力。更多细节，将在后续研究中进一步阐述。

4 结论

本文首先针对地面战场上存在的复杂障碍场，分析了传统人工势场法中最小外接圆(球)描述障碍体的不足，引入了多边形的概念来描述复杂障碍体，以降低障碍场通道变窄和堵死的概率；其次，着重研究了多智能体系统集群避障过程中智能体与障碍体之间的相互作用，基于智能体外心与障碍体外心的距离确定障碍体是否处于激活状态，基于智能体外心与障碍体内心的连线确定激活障碍体的激活边，给出了作用力的表达式；再次，分析了直线型边界的捕获现象及其产生原因，提出采用临时目标的方式绕过捕获边从而克服了捕获现象，介绍了离散化求解方法和模型中关键参数选取的规则；最后，给出了仿真分析结果，验证了不论目标处于静态或动态，本文避障模型都可以实现复杂障碍场下的集群避障控制。

实际上，多边形(多面体)直边(面)捕获问题就是一种局部极小值点问题。由于直边捕获问题属于多边形障碍体建模的衍生问题，本文给出了逃离方法；其他类型的局部极小值问题，各种处理方法很多，比如分层控制、调参、改进势场函数等等，本文不再赘述。

同样，通过仿真结果，可以了解到智能体集群的分离、结合和挤压行为。障碍物的出现可能使智能体集群分离为更多的集群，从而失去相互联系改变原有的网络拓扑。因此，在解决智能体集群避障时，必须解决在切换拓扑网络中有限通信的集群决策问题，这是目前相当有挑战性的课题。