基于马尔可夫链的军用Ad hoc网络可用性建模
傅妍芳, 王赞, 苏一昶, 戴飞, 钟联炯, 郭登登, 卢颖, 梁洪涛
(1.西安工业大学 计算机科学与工程学院, 西安 710021; 2.陕西师范大学 物理学与信息技术学院, 西安 710119)
0 引言
自1991年海湾战争以来,现代战争的作战模式已然发生了极大的变化。美国国防预先研究计划局(DARPA)正在发展名为“马赛克”作战的新作战概念,提出由传统上单一平台提供的整体式杀伤链功能,向由多种杀伤链组成的动态分布式网络作战效果发展。随着这场军事的变革,军用通信网络的规模和复杂程度日益扩大,军事通信业务迅猛增长,尤其由无线移动节点组成的多跳、无中心、能量有限、临时的分布式协同网络(移动Ad hoc网络),其可用性的建模与验证评估的需求也越来越迫切,建立高可用性的网络是准确、及时进行信息交换的基础,从而满足网络系统适应面向各类用户提供高可靠服务的需求。因此,研究基于不同环境条件下多种网络参数的分布式协同网络可用性技术,通过可用性分析信息统一建模与表达,构建新一代分布式作战网络可用性定量评估模型,提升新作战概念下多平台信息交互及战术协同能力,确保系统服务效能的发挥及稳定可靠运行能力的形成。
军用网络传统可用性概念是可靠性理论中一个度量可靠性指标。可靠性只能反映出网络系统或者组件出现故障的概率,而可用性考虑了网络的可修复能力,更能反映出网络的品质。因此,分析战术通信网系统的可用性是衡量系统组网设计优劣、系统稳定性以及系统维护能力的一个重要指标。网络可用性是评估网络质量好坏的一个重要标准,它是对网络中节点可靠性、链路质量可靠性、网络拓扑、业务流量、路由算法等因素的一个综合评价,反映了网络在不考虑外来破坏性作用的情况下节点间能够提供可持续性服务的能力。
现如今,国内对可用性的研究大都是针对复杂系统的工程能力:冯海林[1]研究了网络系统中的可靠性以及可用性,并分析计算了其稳态可用度;张静乐[2]针对电商系统建立了基于随机Petri的可用性模型。
在网络可用性的研究方面:Yin等[3]指出对网络可靠性的研究应该从环境与业务等不同剖面进行分析;董海青等[4-6]研究了基于业务的网络可用性指标,从用户的角度出发,考量了计算机网络满足用户需求的能力,提出影响网络的性能的主要指标包括传输延时、延时抖动、吞吐量、丢包率等参数,并对网络可用性的分析做了一些探索。
为了研究移动Ad hoc网络的定量评估问题,需要认真关注移动Ad hoc网络的时变参数,包括链路负载、路由长度、延迟、移动性等,而早期的大部分研究工作都是针对具体的单个参数进行的。
考虑到节点的移动性,Cho等[7]研究了恒定速度模型下、单跳情况下链路持续时间的平均值,并推广到多跳情况下;Liu等[8]使用随机路点移动模型研究了源节点和目标节点为固定双跳移动自组网(MANET)的链路持续时间机制;Guo等[9]提出了一种利用神经网络方法预测每包单跳平均延迟的方案,然后节点使用预测的1跳延迟参与路由信息扩散;Tickoo等[10]从延迟和队列长度方面分析了IEEE 802.11 MAC的性能,还评估了IEEE 802.11 MAC支持延迟敏感流量的能力,并发现延迟主要是与每个包传输相关的信道访问和保留时间有关。该方面文献重点开展了移动特性在链路持续时间机制和单跳中继的建模研究。
Bisnik等[11]推导了基于开放G/G/1排队网络的多跳无线自组网分析模型,利用扩散近似法求解开放排队网络,推导出MANET端到端平均时延的封闭表达式,并得到了最大可实现吞吐量的表达式。文献[12]在有损链路和有限缓存的情况下,提出了一种两跳中继-f冗余路由策略的中继节点选择策略;文献[13]提出了一种应用于多跳网络、基于协作节点可以自发帮助转发数据包以提升系统性能的机制,在该机制中,分别研究信道优劣、节点Buffer长度和节点个数对整个系统的影响。
本文根据网络可用性的定义,考虑了移动Ad hoc网络节点的移动、故障、传输协议以及中继节点选择策略等影响因素,针对移动Ad hoc网络端到端的通信,提出了一种基于延时的业务性能定量评估模型,并通过移动Ad hoc网络节点的移动特性建立了基于多跳的业务可用性模型,提升了军用网络适应多维度服务的能力,并确保军用网络服务效能的发挥及稳定可靠运行能力的形成。
1 基于故障的马尔可夫可用性建模
1.1 Ad hoc网络故障类型分析
在军用通信网络系统的规划、论证、方案设计与优化方面,军用通信网络的安全性、可靠性问题显得尤为重要。造成军用通信网络战时出现故障的因素较多,可划分为3个层次上的主要原因类型:
1) 在作战过程中,部分战术通信网络因战线推移或其他战事需要实施战术转移或替换,由于通信节点移动或维修等问题导致网络的持续工作能力和重组能力变差导致连接中断为1类故障。
2)通信网络系统在战场上受地形、环境等原因造成的节点间通信链路阻断、信号衰落、噪声等引发的通信链路故障,随机或突发的战场软杀伤为2类故障[14]。
3) 作战过程中出现硬杀伤,包括指控系统及其重要组成部分通信网络成为敌方首选的击毁目标;指挥机构、指控车辆、干线节点等在作战过程中由于电磁辐射密集暴露而击毁;由于大量精制导武器的使用,使得通信网络及其主要组成部件被发现直接摧毁。或者设备的自然损伤或故障,这类称之为3类故障。3类故障因其发生概率较小、故障恢复时间较大而忽略不计。
1.2 移动模型
移动模型是用移动实体移动轨迹的一组规则来表示。作战网络的移动模式与人类日常生活和移动车辆的移动模式各不相同。一个综合移动模型应该是代表性和简单性的一个很好折衷,也就是说,它应该考虑某一运动模式的显著特征,而忽略次要的细节。目前主要移动性模型包括随机路点、参考点群、曼哈顿网格、高斯马尔可夫模型等。为了进行模拟和分析,移动性模拟也应该是轻量级的,这样就可以方便地与网络模拟集成,本文采用的是随机路点移动模型。
根据Ad hoc网络的特点,建立如图1所示的网络模型,网络中节点均匀分布且节点的运动相互独立。A、B、C是一个作战区域的3个子区域,a1、a2是区域A的节点,z1、z2是区域A、B的中继节点,b1是区域B的节点,c1、c2、c3是区域C的节点,z3是区域B、C的中继节点。为简化分析,假设每个移动终端节点通信半径相同并且同一区域内的节点可以直接通信,而位于不同区域的节点由于通信半径的限制无法直接通信。例如,节点a1与节点b1通信时,需要通过中继结点z1或z2.当中继区域存在多个节点时,需要一种可以选出最合适中继节点的选择策略。
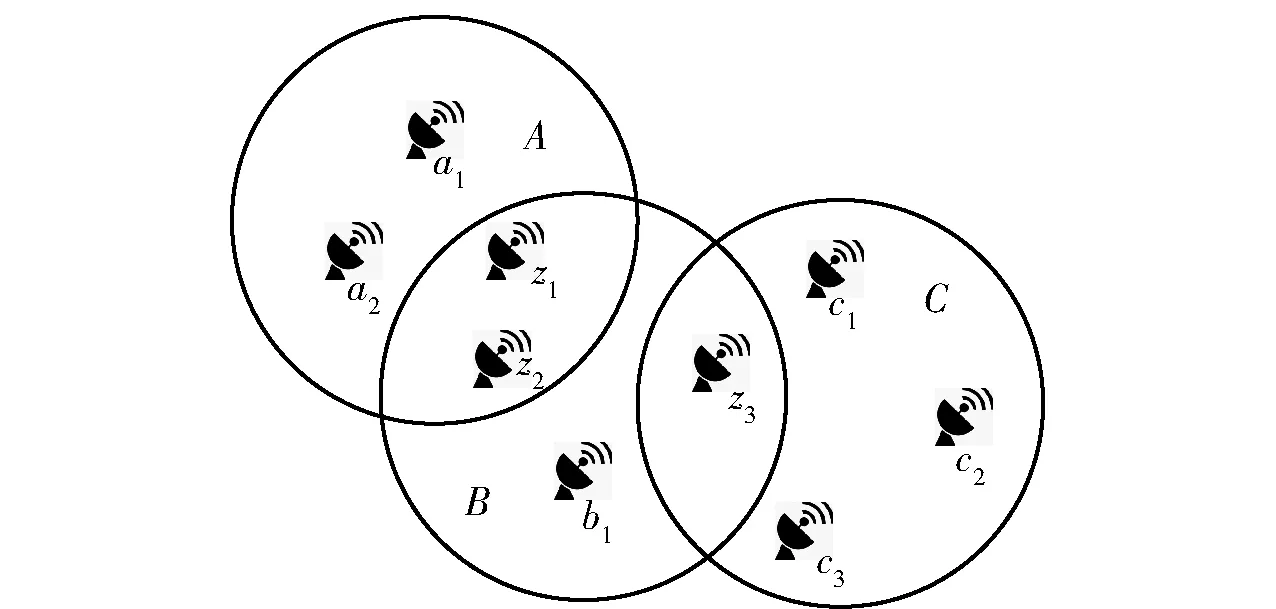
图1 Adhoc中继基本模型Fig.1 Ad hoc relay basic model
1.3 移动Ad hoc网络可用性定义
传统可用性的定义为:产品在任意时刻需要和开始执行任务时,处于可工作或可使用状态的程度,可用性的概率度量称为可用度。
Ad hoc网络可用性目前没有公认的定义,在由两个以上网簇(子网)通过交互区的中间交换节点组成的自组网中,其交互区的所有交换节点或坏或移出交互区,两个子网就成为两个孤岛。尽管网簇内的节点还能通信,但在本质上已不能认为是能互联的移动自组网了。
基于以上观点,根据传统可用性的定义,结合Ad hoc网络特性,则Ad hoc网络可用性的定义可以描述为:Adhoc网络的网簇间公共交换区有存活节点可提供中继能力,使网簇间构成一个互通完整网络的程度,其概率度量称为Adhoc网络的可用度。
1.4 马尔可夫链模型
移动Ad hoc通信网络系统是一个多状态马尔可夫可修复系统。系统由若干个网络节点和若干个修理设备组成,每个节点的寿命分布均为1-e-λft,t≥0,λf>0,节点故障后的修理时间均为1-e-μft,t≥0,μf>0,所有这些随机变量相互独立,故障节点经修理后,其寿命与新的节点一样。本文所采用的可用性模型为n中取g的表决系统模型,n为网络系统中的节点总数,g为正常或者故障的节点个数。n中取g表决系统模型有两类:一类为n中取g个好的节点系统,意思是组成系统的n个单元中有g个或者g个以上完好,系统才能正常工作,记为g/n[G];另一类为n中取g个坏的系统,意思是组成系统的n个单元中有g个或者g个以上失效,系统就不能正常工作,记为g/n[F][15]。本文所采用的是第2类——g/n[F]系统,当故障节点小于g个时,系统正常工作并且修复故障节点;当有g个节点故障时,系统出现故障,这时剩下正常工作的节点也停止工作,不会发生故障,直到正在修理的节点修理好一个,又有小于g个故障节点,系统重新工作[16]。为简化分析,给出以下条件:
1)所有节点移动、1类故障(节点故障)、2类故障(链路故障)等事件相互独立;
2)所有独立事件发生的概率服从负指数分布;
3)1类、2类故障转换时延较小,在转换延迟期间没有额外的节点移入移出事件发生。
为评估图1所示的Ad Hoc网络端到端通信的可用性,选择1跳通信线路a1↔zi↔b1进行分析,此时,通信系统的主要影响因素有a1,z={zi|1,2,3,…,n}和b1,其中z集合中的N个节点都可能成为a1到b1通信的中继结点,i表示当前位于交叉区域并可供正常连接使用的中继节点个数,i∈I={1,2,3,…,N}。设J为故障类型,J={0,1,2},0为无故障,1为1类故障,2为2类故障。二元组{(i,j)|i∈I,j∈J}表示a1↔zi↔b1连接有效(或失效)时,当前交叉区域有i个(包括zi)可供中继的正常节点,并且同时系统处于j类故障状态[17]。
例如,状态(1,0)表示当前网络工作状态正常并且交叉区域只有一个中继节点参与中继转发;状态(N,0)则表示网络工作状态正常,N个中继节点位于交叉区域都能正常工作。当其中未参与中继转发的节点移出交叉区域时,网络状态转移到(N-1,0);当正在参与中继转发的节点移出交叉区域时,网络状态转移到(N-1,1);当中继节点的通信链路受到干扰而导致中断时,网络状态转移到(N-1,2)。
由此可给各个状态分配转换概率,各个状态与转换概率的集合就转化为一个连续时间的马尔可夫链,如图2所示。
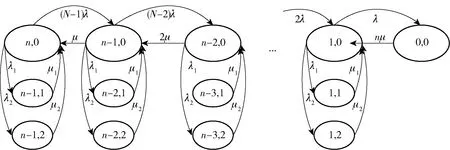
图2 马尔可夫状态转换图Fig.2 Markov states transition diagram
根据故障转换延迟的长短,将故障类型作简化为:
1)考虑节点的移动性,节点的平均移出率是λ,平均移入率为μ;
2)1类故障的发生间隔时间期望值是λf,1类故障维修时间期值是μf;
3)2类故障的发生间隔时间期望值是λs,2类故障维修时间期值是μs;

2 可用度分析
2.1 单跳端到端可用度分析
稳态可用度是马尔可夫可修系统的可靠性特征量之一,其含义是当网络运行达到稳态时,网络在整个运行时间内处于正常工作的时间所占的比例,也就是网络在整个运行过程中处于连通状态的概率。
1类故障的发生间隔时间期望值为λf,2类故障的发生间隔时间期望值为λs,并且λf+λs=1;用二元组{(i,j)|i∈I,j∈J}表示源节点↔中继节点↔目的节点连接的网络可用状态,计算网络业务的可用度,其中对(n,0)有:
(1)
式中:πn,0为网络处于状态(n,0)时的稳态可用度。因此通过一次中继网络端到端的稳态可用度为
(2)
2.2 多跳网络的可用度分析
图3为Ad hoc网络的多跳传输模型,数据包从源节点出发经中继结点最终成功传输给目的节点的稳态可用度计算可通过(2)式计算。
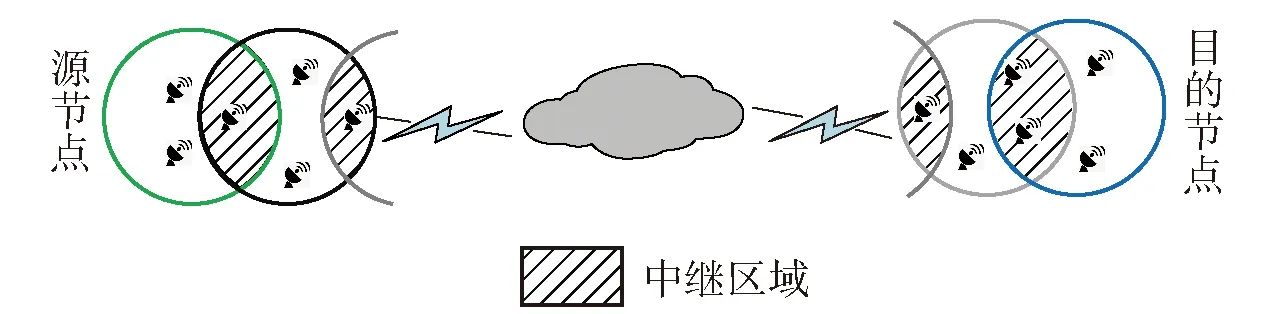
图3 多跳传输模型Fig.3 Multi-hop transmission model

通过理论简化,为了计算多次中继通信网络端到端的稳态可用度,可以将这次网络中存在的多次中继稳态可用度进行综合,当然各跳所占的比重有差别,即
(3)
式中:Δ1为1跳情况下网络系统中所占的比重;A2为2跳的稳态可用度,Δ2为该情况下网络系统中所占的比重;Ak为k跳的情况下的稳态可用度,Δk为该情况下在网络系统中所占的比重。
2.3 中继节点选择策略
中继区域往往有多个中继节点存在,中继节点的选择策略对网络的性能有着至关重要的影响。因此,本文根据所建立的网络可用性模型的特点,从节点故障的角度出发,结合节点的负载开销和饱和度两方面的限制,提出了一种基于瞬时失效率的中继节点选择策略。
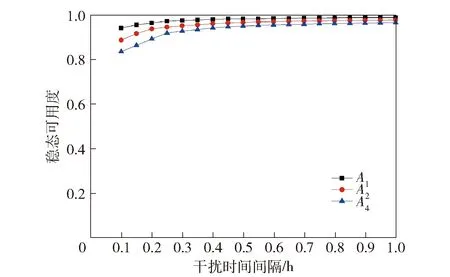
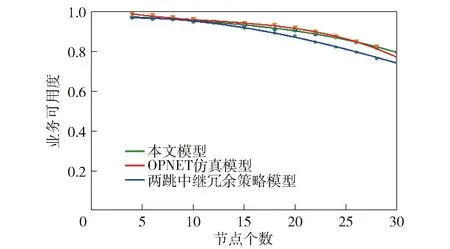
负载方面的限制可表示为0 (4) 式中:li为中继节点i上层业务的负载开销;lt为中继节点的负载阈值,负载开销不能超过负载阈值;pli为节点i负载开销的合格率,如果pli≤0,则该中继节点不参与数据包的转发。 瞬时失效率qi为x时刻还在正常工作的产品中,在x时刻后Δx时间间隔内有多大概率的发生故障,导致产品不能正常工作, (5) 式中:A(x)是网络的稳态可用度,x是中继节点i已经工作时间,由于每次节点故障修复后,节点寿命与新的一样,即x从0 s时刻开始重新计时,所以每个节点的实际工作时间是不一样的,qi也具有差异性。 节点饱和度方面的限制可表示为:当节点饱和时,si=1,当节点处于空闲状态时,si=ε,ε是一个非常接近于0的很小值,防止计算结果出现0. 结合瞬时失效率qi、负载开销li和中继节点饱和度si计算出定义中继节点选择策略的目标函数Q(0 (6) 根据当前时刻中继节点i瞬时故障率对中继节点优先级排序,Qi越小优先级越高,数据包在每次发送时,优先选择Qi最小的中继节点,当该中继节点繁忙时,选择次优节点,依次类推。 在一子网内,节点对信道的占用机制通常为CSMA/CA通信机制。本研究是通过对CSMA/CA通信机制进行定量分析来讨论受网络性能影响的网络可用度问题。通过参考文献[18-19],建立以下假设: 1)满足饱和条件。即每一个节点都总是有将要需要发送的数据包; 2)信道中没有隐藏的网络节点,是理想化的信道; 3)n个网络节点争用同一个接入信道传输数据。 基于上述假设,根据马尔可夫模型对单一网络节点行为的研究,得到网络节点在一个随机时隙内传输发生冲突的概率P与传输数据包的稳态概率τ. 有n个相互竞争处于饱和状态下的节点,每次发送成功后,每个节点都有一个准备发送的数据包。此外,所有的数据包都是连续的,每个数据包在发送之前都有一个随机的回避时间以减少发生冲突的概率。 CSMA/CA采用的离散时间回避机制是指数回避机制,在每个包的传输中,回避时间均匀地选择在(0,w-1)范围内。w的值称为竞争窗口,竞争窗口的大小取决于包发送失败的次数[20]。不管重发次数,每个包尝试发送时,发生冲突的概率是P.w0为最小竞争窗口,wm=2mw0,m为发送失败回退阶数,m∈[0,M],M为最大回避阶数。 由于所有的站点只有在回退计数器为0时才传输包,因此得到稳态概率τ的值。τ和P分别为 (7) P=1-(1-τ)n-1, (8) 式中:(1-τ)n-1为其他n-1个节点都不传输数据包的概率,用迭代逼近法可求取τ和P. 根据τ和P,计算每一轮平均回退窗口: (9) Ps=nτ(1-τ)n-1, (10) PN=(1-τ)n, (11) Pc=1-Ps-PN, (12) 式中:Ps为每一轮发数据包成功传输的概率;PN为数据包不传输的概率;Pc为数据包传输但发生冲突的概率。 当计算每一轮发报文平均回退时间是和每一轮发报文平均回退窗大小、时隙时长等因素相关。延迟时间由(12)式计算得到: (13) 式中:Ebm为每一轮发报文平均回退时间;Ts为数据包成功传输时信道处于通道忙碌状态的时间;Lγ=Ebγ+Tc+T0,Tc为数据包传输发生冲突时通道忙的时间。 报文的平均传输延迟概率分布率是Pm=P(1-P)m,当发送M次都发生冲突不成功时,终止发送报告上层相应m-1次冲突后,报文发送成功,其报文的传输延迟时间是Em,其中对所有的Em≤TB,TB为军用网络时延的战技指标。 (14) 式中:u为跳数,u∈[0,k];F1为1跳的时延达标率。多跳平均时延达标率为 (15) 应用统计学原理,建立了基于时延的业务可用度模型,即将网络业务性能(多跳平均时延)达标率和稳态可用度进行综合运算,则得到整个战术通信网络的业务可用度。 为验证上述模型在通信网络中的正确性和实用性,本节参照图1所示的网络模型进行仿真实验,设计了多组实验并与理论计算结果进行对比。本实验仿真对象是执行作战任务的战术小分队,分队由20个单兵组成,每个单兵都装备Ad hoc通信设备,均匀分布于20 km×20 km的平面区域,无线电台通信半径为2 km,作战半径为4 km,节点最大移动速度为5 km/h,信道传输速率2 Mbit/s,中继最大值为4跳。其中所有节点的运动均按照随机路点移动模型进行仿真。 通过对军用移动自组织网络可用性建模理论的研究,进行了建模和仿真实验,其参数如表1和表2所示。 表1 可用度基本参数 表2 业务可用度参数 各实验根据Ad hoc网络特点以及建模时分析的故障类型,输入节点发生故障的时间间隔以及故障维修时间,链路故障发生的时间以及修复时间,节点因功耗问题出故障的恢复时间等参数,最终计算出当前条件下网络的稳态可用度,然后在CSMA/CA通信机制的业务可用度参数计算出基于传输时延的可用度值。以下实验采用表2中的具体数值,并通过对照仿真结果,比较在不同实际网络参数对网络可用性的影响。 首先通过大量实验模拟军用Ad hoc网络在不同干扰时间间隔对可用度的影响。在不同的干扰时间间隔实验下,网络稳态可用度的计算结果如图4所示。然后根据模型算法将稳态可用度和时延达标率进行量化后可以计算得到基于传输时延的业务可用度,结果如表3所示。从模型算法结果可以看出,在干扰频率超出一定界限时,网络的稳态可用度急剧下降,并且受干扰的影响随节点数的增加变大。 图4 稳态可用度仿真结果Fig.4 Simulated results of steady state availability 表3 可用度量化表 在相同环境参数的条件下,也进行仿真实验,实验数据与本文模型数据非常接近(见图5)。同时也表明了在干扰时间间隔发生变化时,随着干扰时间间隔的增大,时延的业务可用度也在增大的实验现象。 图5 干扰时间间隔对可用度的影响Fig.5 Effect of interference time interval on availability 考量在中继区域的节点选择对网络可用性的影响,本文提出的可用性评估模型中分别采用基于2跳中继冗余策略和基于瞬时失效率的中继节点选择策略,并与仿真实验进行可用度数值分析。在不同节点个数的网络情况下,分别针对基于2跳中继冗余策略模型和本文模型与仿真结果进行比对,结果如图6所示。 图6 节点个数对可用度的影响Fig.6 Effect of the number of nodes on availability 对比数据反映了作战区域内节点个数与业务可用度的关系,随着节点个数的增加,时延的达标率降低,基于时延的业务可用度会变小。此外,通过拟合度检验方法得出基于失效率的中继选择策略与仿真实验的拟合度较高。说明中继节点若发生故障而维修,将会影响节点之间的传输连续性,同时,若数据传输流量较大,中继节点容易满足饱和条件,通过选择空闲中继节点发出数据,网络可用度更高。 针对信道传输速率和报文长度两个因素分别对Ad hoc网络可用性进行分析。实验结果(见图7)反映了信道传输速率与业务可用度的关系。并通过趋势可以看出信道传输速率越快,传输时间越短,节点之间的时延就越小,时延达标率就越高。因此随着信道传输速率的增加,基于时延的业务可用度也就越大。 图7 信道传输速率对可用度的影响Fig.7 Effect of channel transmission rate on availability 实验结果(见图8)反映了报文长度与业务可用度的有紧密的关系。通过数据可以看出报文长度和信道传输速率刚好相反,报文长度越大,传输单个报文所需要的时间也就越多,所以节点之间的时延就越大,时延达标率就越低。因此,随着报文长度的增加,基于时延的业务可用度在变小。 图8 报文长度对可用度的影响Fig.8 Effect of message length on availability 本文分析了移动Ad hoc网络节点的移动特性和作战环境造成的故障因素对网络可用性的影响,建立了基于故障的移动Ad hoc网络马尔可夫可用性模型,并针对中继区域节点的优先选择问题,结合节点的负载开销和饱和度两方面的限制,提出了一种基于瞬时失效率的中继节点选择策略。通过分析基于CSMA/CA的传输机制,研究影响网络业务主要因素的延时模型,建立了基于业务可用度的定量计算方法,计算了基于传输延迟的网络业务可用度。最终以某典型陆军战术分队通信网为例,通过理论建模与仿真实验进行对比,二者之间的数据平均误差小于9%,说明建立的可用性计算模型能够较准确地反映军用Ad hoc网络可用性。3 基于延时的业务可用性评估模型
4 仿真实验结果分析






5 结论

