流体输送管路中悬浮体运动稳定性数值分析

李岚清，李 俊，陈 晔，杨 洹

(四川轻化工大学 机械工程学院，四川 自贡 643000)

引言

流体驱动型管道机器人由于结构简单、无需外部能源供给、作业区间大等优点，在管道清理及检测等方面具有重要作用[1]。目前，典型的流体驱动型管道检测机器人以支撑式为主，该类机器人存在越障能力、过弯性能和管径适应能力差等缺点[2-3]。悬浮式管道机器人以工作流体作为驱动力，能够长距离、在役工作，不受转弯半径的影响，管径适应能力强，可避免支撑式存在的不足，对于实现大型管线的长距离在役检测有重要意义[4]。然而，悬浮式管道检测机器人检测数据的可靠性和准确性受其运动稳定性影响很大，开展相关研究以了解运动稳定性变化规律对于开发相应的机器人至关重要。

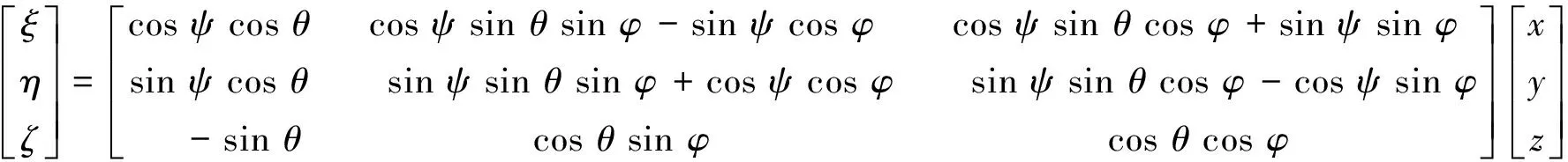
(1)

由于实验条件的限制，国内外学者大多采用CFD软件围绕流体驱动机器人的运动分析展开研究。利用CFD软件通过二维静态仿真得到压差式机器人的驱动力与管内流体压力和流速、机器人与流体之间相对速度的关系，并采用动网格技术模拟了2D与3D的管道机器人启动过程中管壁摩擦力、质量等的影响，但未考虑到机器人自身运动产生的影响[5-8]；ASGHAR T等[9]利用Fluent软件与试验结合分析了清管器的旁路直径、重量等对清管器速度的影响；DIEGO J P等[10-11]利用CFX软件动网格技术通过2D轴对称模型的管道机器人启动过程的研究，得到了机器人质量、湍流模型以及发射时间对机器人稳定速度的影响，得到机器人最终的运动速度要大于平均流速；KHALIL M F等[12]通过CFD软件静态模拟，分析了一种浮体式胶囊运输器在管道流体中表面的压力分布、阻力和升力，对比不同湍流模型的模拟结果，得出升力是由机器人在重力方向上的表面压力积分差引起，忽略了机器人运动的影响；DEREJE E W等[13]在忽略机器人外形对运动影响的情况下，利用DPM模型模拟了自由浮体式机器人在不同倾角管内的运动状况。综上文献研究表明，大量研究主要围绕支撑式的流体驱动机器人本体质量、流体速度、管壁摩擦力等参数对流体驱动型机器人运动速度的影响展开，对悬浮结构的机器人的研究很少，悬浮式管道机器人在动态情况下的运动稳定性研究更少。鉴于此，本研究以城市中常见的给水管线为例，基于CFD对流体驱动下悬浮体的运动过程进行仿真，通过建立在六自由度参数基础上的欧拉角、欧拉角频谱、速度、力和力矩等5个特征量的动态变化规律对悬浮体的稳定性进行研究，以期对悬浮式管道机器人的稳定性控制提供依据。

1 运动模型

1.1 坐标系

为了便于悬浮体的运动分析，本研究采用两种坐标系：固定坐标系E-ξηζ和运动坐标系O-xyz，均为右手系。运动坐标系选择悬浮体的重心为原点，O-x轴指向悬浮体首端，O-y轴指向悬浮体右端，O-z轴指向悬浮体底部。固定坐标系为惯性坐标系，通常以大地作为参考系，研究选择悬浮体的起始位置点为坐标原点，三轴的正方向与运动坐标系的初始方向一致。坐标系如图1所示[14-16]。两坐标之间的转换关系式见式(1)：

图1 坐标系及六自由度参数定义

式中，ξ，η，ζ—— 悬浮体在固定坐标系下的坐标

x，y，z—— 悬浮体在运动坐标下的坐标

φ，θ，ψ—— 悬浮体欧拉角：滚动角、俯仰角和偏航角

1.2 运动方程

悬浮体随流体在管道内运动，运动的速度、位移和姿态等随时间动态变化，为了研究悬浮体的稳定性变化规律，本研究在运动坐标系下，对各矢量的变化以及动力学方程[17-20]进行计算。

2 边界条件及数值计算

本研究中边界条件及模型参数见表1，悬浮体重心位置(0,0,0.015 m)，重心的主惯性力矩为(Jx,Jy,Jz)=(0.00171,0.00465,0.00375 kgm2)；重力加速度向量为(0,0,9.81 m/s2)；悬浮体起始速度为0；管材为PVC，外径160 mm，总长12.5 m，初始位置距离入口长2 m；采用Realizablek-ε湍流模型。

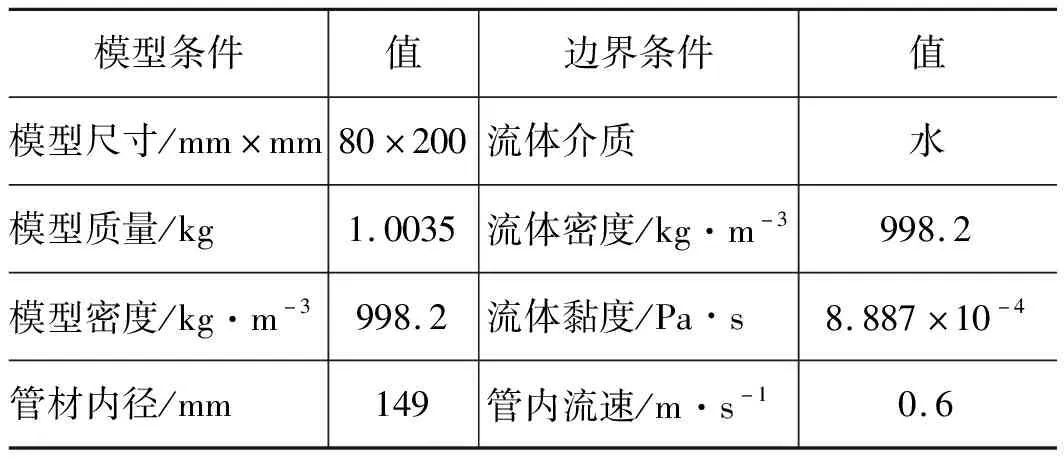
表1 边界条件及模型参数

模型采用重叠网格模型进行划分与模拟计算，悬浮体及周围流场作为嵌套组件，采用多面体网格划分，网格尺寸大小为3 mm；整个管道流场作为背景网格，采用多边形网格扫描进行网格划分，网格大小为6 mm，总体网格数为309万。具体细节请见图2，其中A为起始点，B,C,D分别为三个弯头区域，B1和B2,C1和C2,D1和D2分别为各弯头的进出口点，E为管道出口。

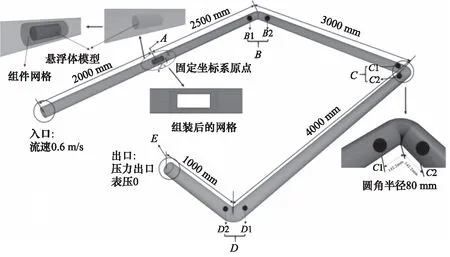
图2 模型及网格

3 结果分析

本研究通过仿真了解悬浮体在管线内运动过程中的稳定性，以便于设计出稳定可靠的悬浮式流体驱动管道机器人。悬浮式机器人的稳定性主要涉及到绕运动坐标系三轴的转动角度变化规律，以及沿管径方向的位移变化。由于沿管径方向的位移变化只能通过运动坐标系下三轴方向线速度分量经坐标转换(式(1))后，再对时间积分计算得到，故需要对线速度的变化规律进行分析；同时，速度的变化规律在一定程度上也可为判断检测设备频率是否能满足使用要求提供选择依据。为了后续对悬浮体的运动控制进行研究，故需对力与力矩大小及其变化规律的分析。

因此，本研究中悬浮体运动稳定性选择以下5个量来反映：欧拉角(φ，θ和ψ)、欧拉角变化的频谱规律、速度(线速度：u，v和w；角速度：q，p和r)、力(X，Y和Z)和力矩(K，M和N)。

3.1 受力及力矩变化规律

悬浮体在管内的运动状态与受力主要受流体流动方向与速度的影响，见图3。当悬浮体速度小于流体速度时，运动主要由本体前后端的压差力驱动，见图3a；当悬浮体速度与流体速度接近时，前后表面压差较小，运动主要随流体运动，见图3b；当悬浮体转弯时，由于流体与悬浮体的运动方向发生突变，导致悬浮体表面前端局部压力大于尾部，产生与运动方向相反的压差力，见图3c。

图3 悬浮体各运动阶段周围流场压力分布图

监测悬浮体在运动过程中，分别在x，y，z三轴方向上受到的各分力和力矩的变化情况，见图4。可以看到，在某些时间点上悬浮体的受力和力矩存在大的突变，而B，C和D的弯头区域内出现突变次数最多，这是由于悬浮体在运动过程中存在碰撞管壁的状况引起的，这种状况直接改变悬浮体的运动状态，从而影响悬浮体的运动稳定性，以下分析均不考虑悬浮体碰壁时引起的力和力矩的突变。悬浮体在整个运动过程中，其受力大小均小于2 N，力矩均小于0.1 Nm，这表明悬浮体在管内运动的受力与力矩较小，有利于对其进行稳定性的控制。

如图4a所示，悬浮体沿O-y和O-z方向的受力Y和Z从B1～E点的运动过程中均存在周期性波动，说明悬浮体在这两个方向上均存在运动稳定性不太好的情况，其中Y的波动幅度明显远大于Z，说明悬浮体在O-y方向上的运动稳定性比O-z方向差很多；Y和Z的波动幅度在B，C和D3个弯头区域均较大，说明在该区域内运动稳定性最差；悬浮体出弯后，随离B2，C2和D2距离的增加，波动幅度逐渐减小，说明运动稳定性逐渐变好。

如图4b所示，悬浮体绕O-x轴的转动力矩K从B1～E点的运动过程中存在波动幅度较大的周期性波动，说明悬浮体在该方向上的转动幅度较大，且呈现周期性，转动稳定性差。力矩K，M和N的波动幅度均在B，C和D弯头区域内达到最大值，说明悬浮体在弯头区域内的转动幅度最大，转动稳定性最差；出弯后的B2～C1，C2～D1和D2～E段，K的波动幅度明显大于M，且两者的波动幅度均随运动距离的增加逐渐减小，绕O-z轴的转动力矩N无明显变化，说明在出弯后的悬浮体绕O-x轴的转动稳定性最差，但随运动距离的增加逐渐变好，绕O-z轴的转动不明显，稳定性较好。

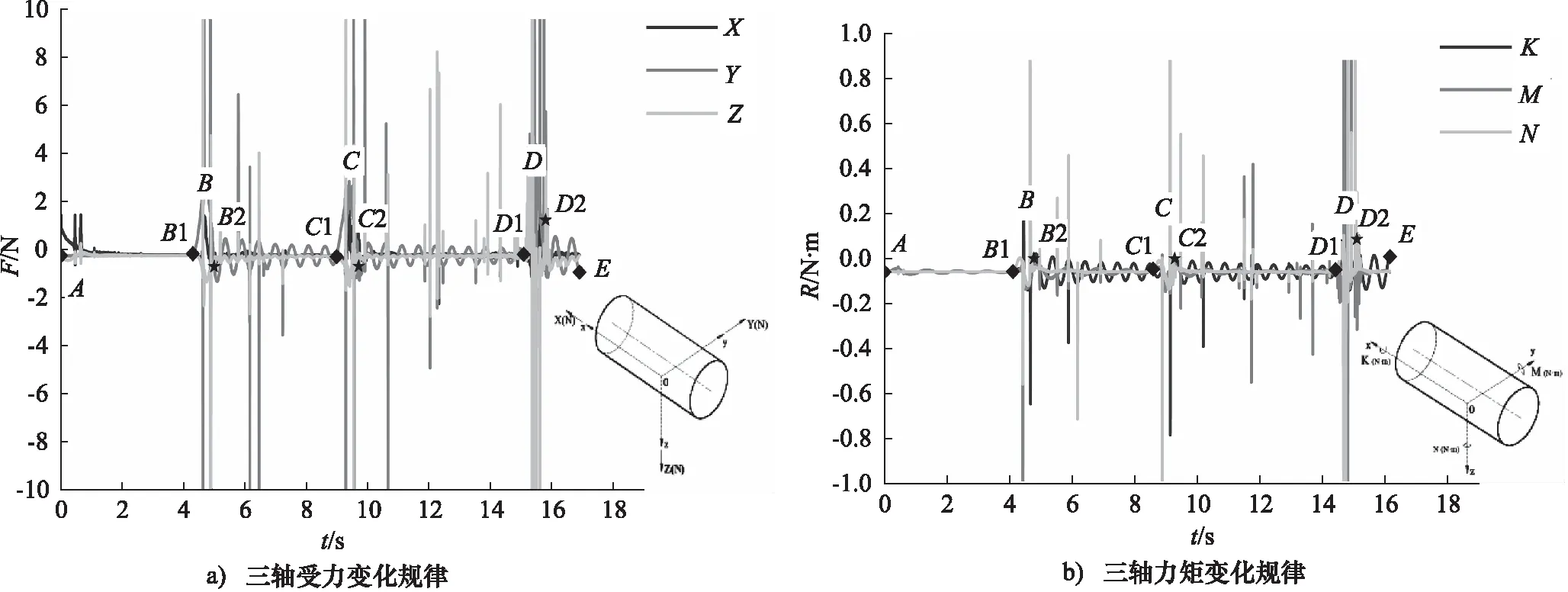
图4 运动坐标系下力与力矩的变化规律

因此悬浮体的运动稳定性可从以下两方面进行分析，由好到差的顺序分别为：

(1)平移：x>z>y，在弯头区：入弯前>出弯后>弯头；

(2)转动：z>y>x；在弯头区：入弯前>出弯后>弯头。

3.2 姿态变化规律

流体驱动下的悬浮体具有6个自由度，由于运动过程中受力与力矩不稳定的原因，运动过程中会绕x，y，z三轴转动，利用转动角度大小及转动角度变化频率反映直观的姿态稳定性。由图5中ψ(偏航角)的变化可以看出，悬浮体在此期间经历过3次90°的弯头分别为B，C和D区域，每次的转弯幅度均大于90°；在出弯后的2.5 s内，ψ(偏航角)都是无规律波动，说明该时间段内悬浮体呈现绕O-z轴平缓的无规律转动，稳定性较差；随后的时间段稳定在固定的角度范围内，说明该时间段稳定性较好。在整个运动过程中，φ(滚动角)和θ(俯仰角)在B1～C1，C1～D1和D1～E段均呈现周期性波动且波动幅度由大变小，而在弯头区域(B，C和D)内，波动幅度达到较大值，最大分别52°和17°，此时位于B区域，说明悬浮体在弯头区域的转动范围大，稳定性差，其中绕O-x轴的稳定性最差；出弯后B2～C1，C2～D1和D2～E段，稳定性随波动幅度的减小而逐渐变好，φ(滚动角)和θ(俯仰角)最小幅度分别为13°和0.5°，此时距离C2点3.72 m 左右。因悬浮体在过弯前后其绕O-x轴转动的φ(滚动角)变化幅度最大，故有必要对其在过弯后大致多远才能恢复平稳运动进行分析，经分析计算得到，过弯后φ(滚动角)波动幅度每米的衰减范围大约为15%～25%，以φ(滚动角)在C2点的波动幅度30.4°为例，悬浮体至少在过弯后6.5 m以上才能衰减到5°以内。这是由于出弯处存在涡流区域，影响范围较大，悬浮体受到绕轴旋转的力矩随离涡流区域距离的增加而减小。

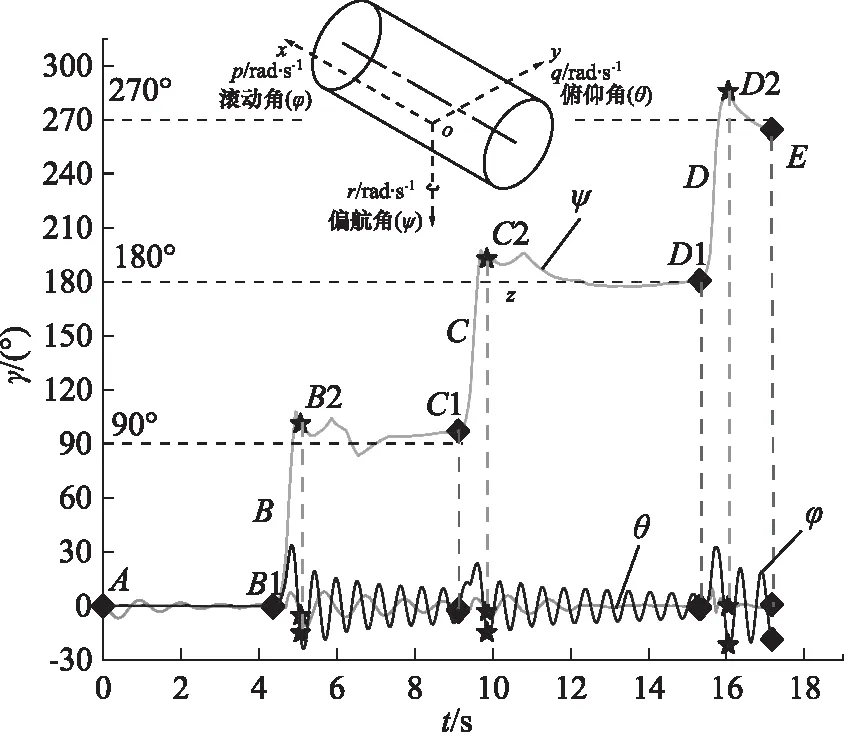
图5 三轴欧拉角变化规律

在运动过程中，考虑到ψ(偏航角)仅在转弯时有较大幅度的波动，其他时候较稳定，因此本研究仅对θ(俯仰角)和φ(滚动角)进行频谱分析，分析结果如图6所示，结果表明，悬浮体运动过程中姿态变化频率主要在3 Hz以下，说明在该研究条件下，悬浮体姿态的总体稳定性较好，这有利于对悬浮体运动状态的控制和环境状态参数的监测。

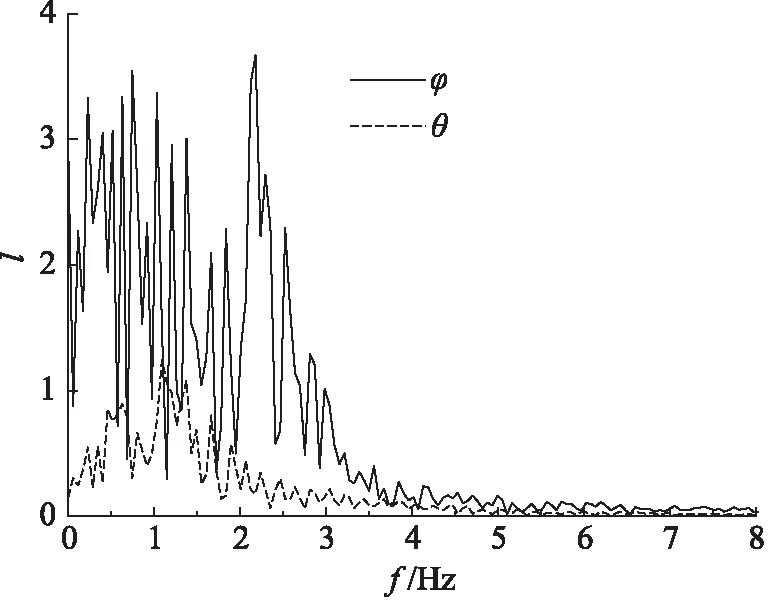
图6 θ(俯仰角)和φ(滚动角)频谱图

因此悬浮体的运动稳定从转动方面进行分析，由好到差为：绕三轴转动：z>y>x，在弯头区：入弯前>出弯后>弯头。经分析计算得到，过弯后φ(滚动角)波动幅度每米的衰减范围大约为15%～25%，本研究中绕O-x轴转动的φ(滚动角)波动幅度至少在过弯后6.5 m以上才能衰减至5°以内。

3.3 悬浮体速度变化规律

速度可分为角速度与线速度，对检测设备的检测速度与准确性有一定影响，同时在x,y,z三轴上的分量分别反映了悬浮体绕x，y，z三轴转动与沿x，y，z三轴运动变化的快慢，见图7。如图7a所示，A～B1段属于悬浮体运动启动阶段，沿O-x轴运动的线速度u变化最明显，初速度由0增加至0.64 m/s；线速度w整体呈现幅度由大到小的周期性波动趋势，说明悬浮体开始沿O-z方向运动位移变化较快，随后减慢，该方向悬浮体的运动稳定性总体较好。线速度u，v和w在B、C和D弯头区域均存在突变的情况，其中u减小，v和w呈现一个周期变化，说明在该区域悬浮体在O-y和O-z方向上的运动稳定性较差，这与悬浮体在转弯过程中与管壁碰撞，导致受力发生变化，见图4a。在B2～C1，C2～D1和D2～E段，线速度u缓慢上升，线速度v和w呈现周期性变化，波动周期呈现为：出弯后>弯头，w>v，其v和w的波动幅度均在出弯后0.7 s内达到最大值，随后w的波动幅度逐渐减小，v波动不稳定，说明在出弯后悬浮体的波动周期大于弯头处，且在O-y方向的运动稳定性比O-z方向差。这是由于出弯处存在涡流区域导致悬浮体运动不稳定。

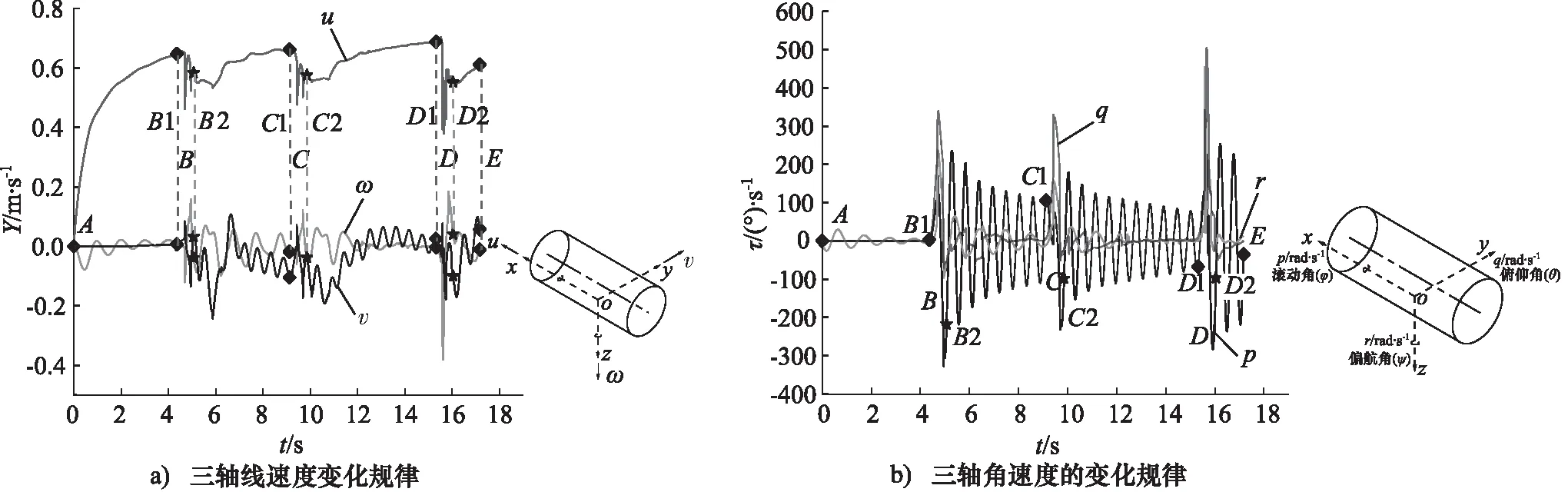
图7 运动坐标系下角速度与线速度变化规律

如图7b所示，角速度p，q和r均在弯头(B，C和D)处发生了较大的变化，其中p，r的变化比q明显。随后在B2～C1，C2～D1和D2～E1区域内三个角速度的波动均逐渐减小，其中C2～D1区域长度为3.72 m，p的波动幅度从388.5°/s降到137.8°/s，每米的衰减度范围大约为15%～25%，依然明显远大于q和r。说明悬浮体在弯头的位置的转动急剧不稳定，此时对检测设备频率的要求较高；出弯后，随运动距离的增加，稳定逐渐变好，但是绕O-x轴转动的稳定性还是明显比O-x和O-y两个方向差很多。

因此悬浮体的运动稳定性可从以下两个方面进行分析，由好到差的顺序分别为：①平移：x>z>y，在弯头区：入弯前>出弯后 >弯头；②转动：绕三轴转动：z>y>x；在弯头区：入弯前>出弯后>弯头。

4 结论

(2)悬浮体出弯后，绕O-x轴转动的φ(滚动角)波动幅度每米的衰减范围大约为15%～25%；

(3)悬浮体的运动稳定性由好到差的顺序分别为：①平移：x>z>y；在弯头区：入弯前>出弯后>弯头；②转动：绕三轴转动：z>y>x；在弯头区：入弯前>出弯后>弯头。