考虑井阻及涂抹作用的非饱和土竖井地基固结解析解*

秦爱芳 许薇芳 李天义

(上海大学土木工程系，上海 200072，中国)

0 引 言

随着大量高速公路、铁路在软土地区开工建设，带动了非饱和土竖井(碎石桩、砂井、塑料排水板等)地基工程实践和理论的进一步发展。在利用竖井固结法进行软土路基处理过程中，发现经过压实的路基填土的饱和度在65%～87%之间，处于非饱和状态，其固结特性与饱和土明显不同。如果利用饱和土固结理论进行设计分析，会与工程实测值产生较大偏差(顾洋洋，2017)，因此需要对非饱和土竖井地基固结特性进行研究。竖井中的水向外排出会受到一定阻力，这种现象称为井阻作用。另外，施工的扰动会导致竖井周围土体渗透性减弱，产生涂抹作用。本文对考虑井阻及涂抹作用的非饱和土竖井地基固结特性展开研究。

饱和土竖井地基固结理论大多基于饱和土地基固结理论(Biot，1941；Terzaghi，1943)。例如，等应变和自由应变轴对称固结理论就是基于该理论建立起来的(Barron，1948)。随后，基于竖井区流量连续条件，得出了考虑井阻和涂抹作用的自由应变的解，进一步完善了Barron自由应变的理论(Yoshikuni et al.，1974)。同时，运用分离变量法得到了接近自由应变条件下严密解的饱和土竖井地基等应变固结解，建立了等应变竖井地基固结理论(谢康和等，1989)。针对多层地基固结问题，采用饱和土理想井问题的求解思路可得到双层饱和土竖井地基固结解析解，对成层土竖井地基固结的研究具有很好的借鉴作用(Tang et al.，2001)。由于涂抹作用引起的径向渗透系数变化会对竖井地基的固结速率产生影响，学者考虑涂抹区土体水平渗透系数呈不同变化模式，得到饱和土竖井地基固结解(陈国红等，2011)。在边界条件方面，由于传统边界通常视为完全渗透或不完全渗透的极限状态，因此对考虑任意荷载双面半透水边界条件下分数阶导数黏弹性饱和土层固结问题进行了研究(李林忠等，2018)，饱和土竖井地基固结理论被不断完善。

由于非饱和土的复杂性，国内外对非饱和土竖井地基固结研究起步相对较晚。基于非饱和土一维固结理论(Fredlund et al.，1979)，采用Laplace变换并引入Bessel方程对非饱和土地基一维固结问题进行研究，得出了非饱和土地基固结半解析解(秦爱芳等，2010)。对于非饱和土竖井地基，通过Laplace变换得到了不同边界条件下的非饱和土竖井地基固结的半解析解(Wang et al.，2017a,2017b)。另外，通过分离变量法得到了考虑涂抹作用的非饱和土竖井地基固结解析解(Ho et al.，2018)。同时，基于等应变模型，引入本征函数法得到了考虑井阻作用的非饱和土竖井地基固结的解析解(Zhou et al.，2018)。

但目前在非饱和土竖井地基固结的研究中，没有同时考虑井阻和涂抹作用的情况。本文建立非饱和土竖井地基等应变固结模型，引入变量Φ1和Φ2将控制方程组转化为线性偏微分方程组，采用分离变量法和待定系数法推导出了同时考虑井阻和涂抹作用的非饱和土竖井地基固结解析解。本研究方法可向任意荷载和井阻随时间变化情况拓展，对非饱和土竖井地基固结的系统研究有一定的参考价值。

1 解析解推导

1.1 基本假设

(1)气相与液相保持连续；

(2)液相与土颗粒不可压缩；

(3)土体的渗透系数及体积变化系数为常数；

(4)竖井内超孔隙压力(超孔隙气压力、超孔隙水压力)沿径向的变化很小，可忽略不计；

(5)等应变条件成立，同一深度土体的竖向变形相等，且竖井地基无侧向变形；

(6)固结过程中发生的应变为小应变。

土体渗透系数及体积变化系数在实际工程中随着地基的固结会发生变化，但考虑这些系数非线性变化将会给解析解的求解带来很大的困难，并且认为小应变及瞬时荷载作用下假定(3)也是可接受的(Fredlund et al.，1979；Ho et al.，2018；秦爱芳等，2019)。

1.2 计算模型

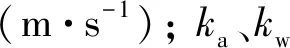
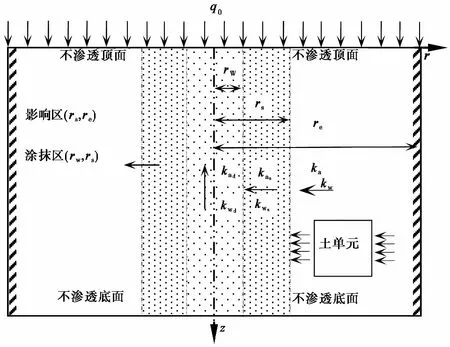
图1 非饱和土竖井地基固结计算模型Fig.1 Consolidation modeling of vertical drain foundations in unsaturated soils

1.3 控制方程

基于Fredlund非饱和土一维固结理论，瞬时荷载作用下非饱和土竖井地基等应变固结过程中超孔隙气压力与超孔隙水压力控制方程表示如下(Zhou et al.，2018)：

(1)

(2)

其中，考虑涂抹作用时(Ho et al.，2018)，

(3)

(4)

1.4 初始条件与边界条件

1.4.1 初始条件

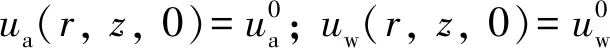
(5)

1.4.2 边界条件

在r=rw处：

uas(rw,z,t)=uad(z,t)

(6a)

uws(rw,z,t)=uwd(z,t)

(6b)

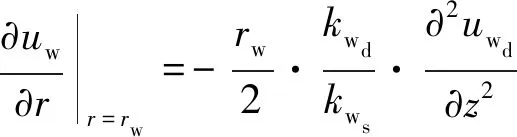
(7a)

(7b)

在r=rs处：

uas(rs,z,t)=ua(rs,z,t)

(8a)

uws(rs,z,t)=uw(rs,z,t)

(8b)

在r=re处：

(9)

在竖井内：

uwd(z,0)=uad(z,0)=0

(10)

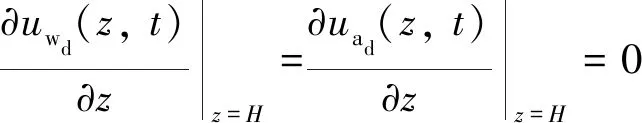
(11)

1.5 解析解推导

将式(1)、式(2)重新整理得：

(12a)

(12b)

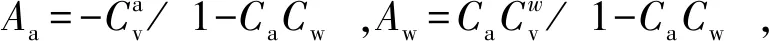
通过引入变量Φ1和Φ2，式(12a)、式(12b)可以被转化为如下等价的线性偏微分方程组，转化过程见附录B：

(13a)

(13b)

式中：

Φ1(r,t)=ua+q21uw，Φ2(r,t)=q12ua+uw

(14)

(15)

将式(13a)、式(13b)对r作两次积分，并带入边界条件(6)、(8)和(9)得：

rw≤r≤rs：

(16a)

(16b)

rs≤r≤re：

(17a)

(17b)

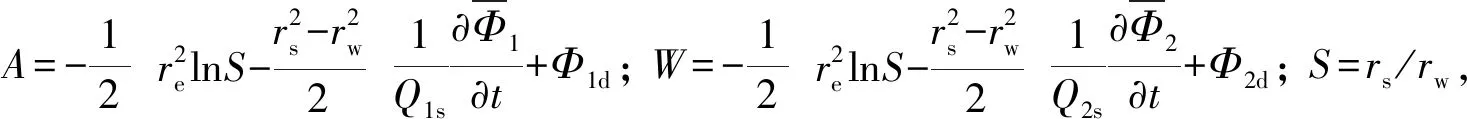
将式(16a)、式(16b)及式(17a)、式(17b)分别带入式(15)得：

(18a)

(18b)

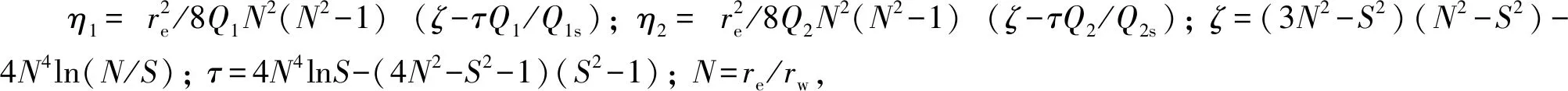
对式(13a)、式(13b)中r作一次积分，并代入边界条件式(7a)、式(7b)整理得：

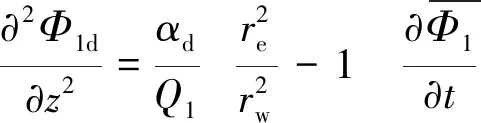
(19a)

(19b)

式中：αd=ka/kad=kw/kwd。

整理方程(18a)、(18b)及(19a)、(19b)可得：

(20a)

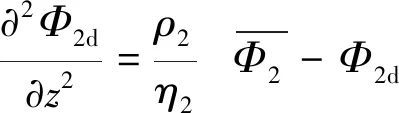
(20b)

式中：ρ1=αd(N2-1)/Q1，ρ2=αd(N2-1)/Q2。

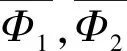
(21a)

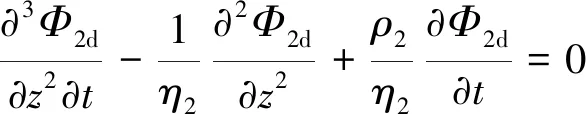
(21b)

采用分离变量法，可得方程(21a)、(21b)的通解为：

Φ1d=(a1sinλz+b1cosλz)e-c1t

(22a)

Φ2d=(a2sinλz+b2cosλz)e-c2t

(22b)

式中：a1，a2，b1，b2，λ为待定系数；c1=λ2/(ρ1-η1λ2)；c2=λ2/(ρ2-η2λ2)。

代入边界条件式(10)，式(11)可得：

(23a)

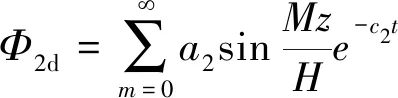
(23b)

式中：M=(2m+1)π/2，m=0,1,2…

G=αd(H/dw)2为井阻因子。

将式(23a)、式(23b)代入式(20a)、式(20b)得：

(24a)

(24b)

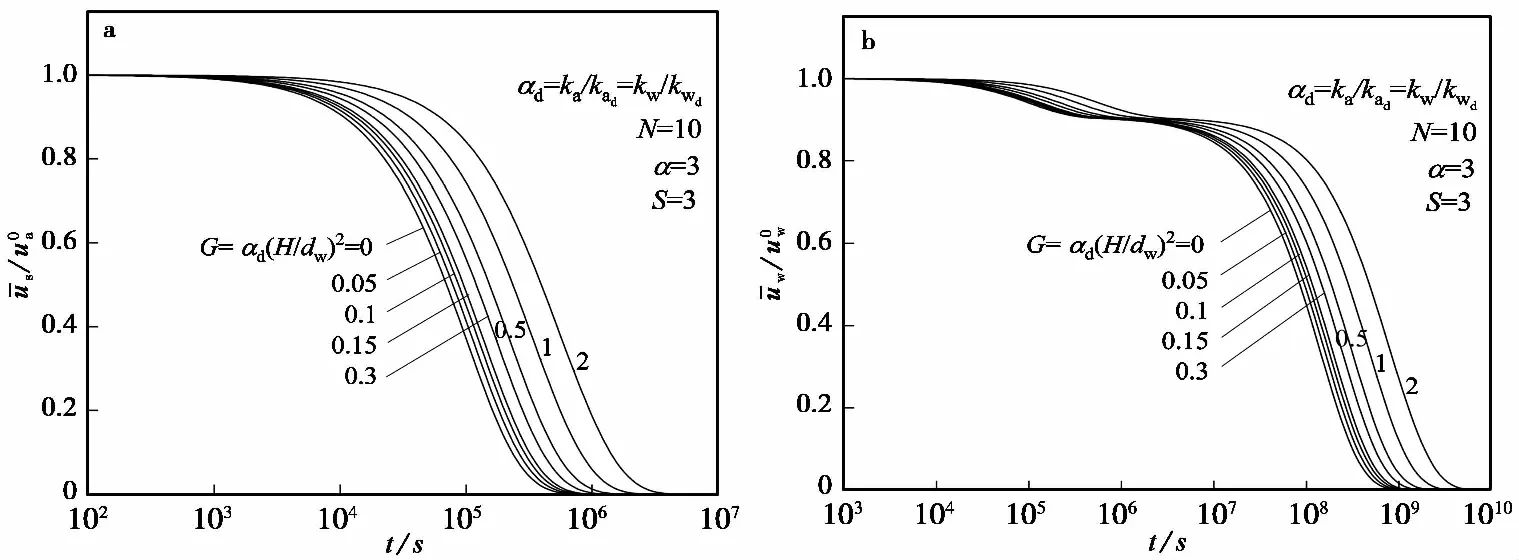
图与在不同G时的消散曲线Fig.2 Dissipation curves of different G

由初始条件式(5)及函数系sin(Mz/H)在区间[0，H]上的正交性，得：

(25a)

(25b)

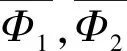
(26a)

(26b)

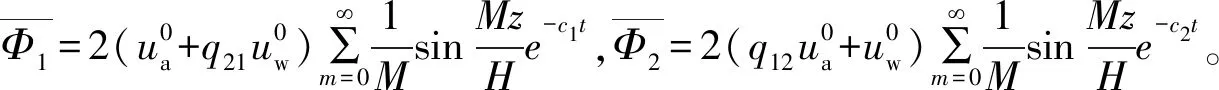
式(26a)、式(26b)为瞬时荷载下考虑涂抹和井阻作用的非饱和土竖井地基等应变固结解析解。

2 验证及算例分析

2.1 验 证

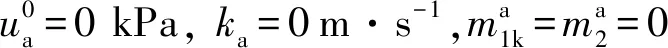
将上述孔隙气参数带入解析解(26a)、(26b)后得到：

(27)

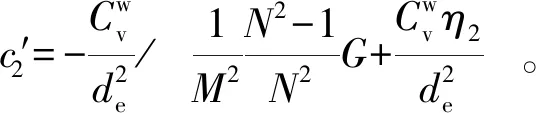
将式(27)与谢康和等(1989)的等应变固结解析解比较发现，两者公式完全相同，验证了本文非饱和土竖井地基等应变固结解的正确性。

2.2 算例分析

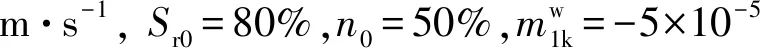
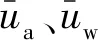
图3a和图3b是考虑井阻作用与不考虑井阻作用(G=0)的竖井平均超孔隙压力的相对偏差Wa、Ww随时间变化的曲线。当G小于0.1时，竖井地基中平均超孔隙压力的相对偏差较小，且消散完成时间基本相同。因此，在实际工程中，当G小于0.1时，建议不考虑井阻作用。

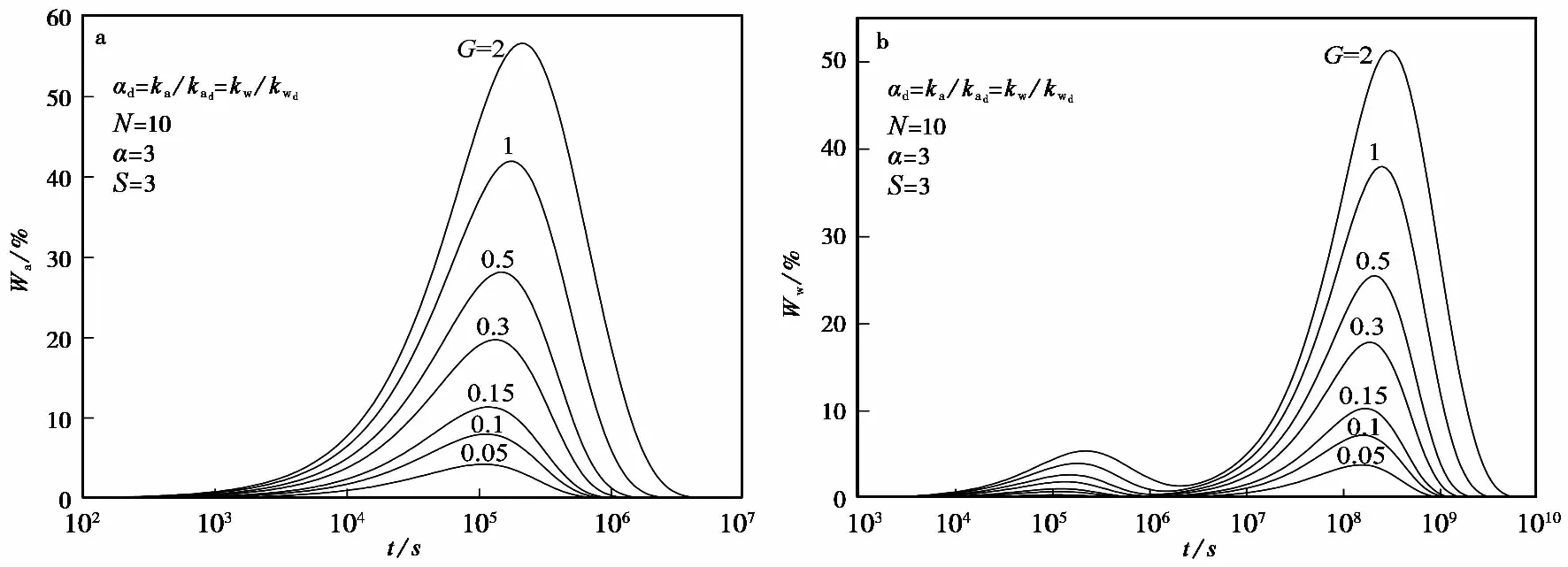
图3 相对偏差Wa、Ww的变化曲线Fig.3 The change curves of relative deviation Wa、Ww

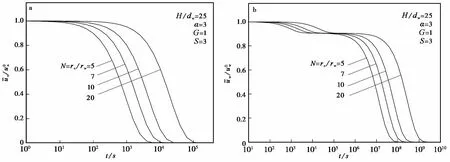
图与在不同N时的消散曲线Fig.4 Dissipation curves of different N

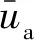
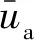
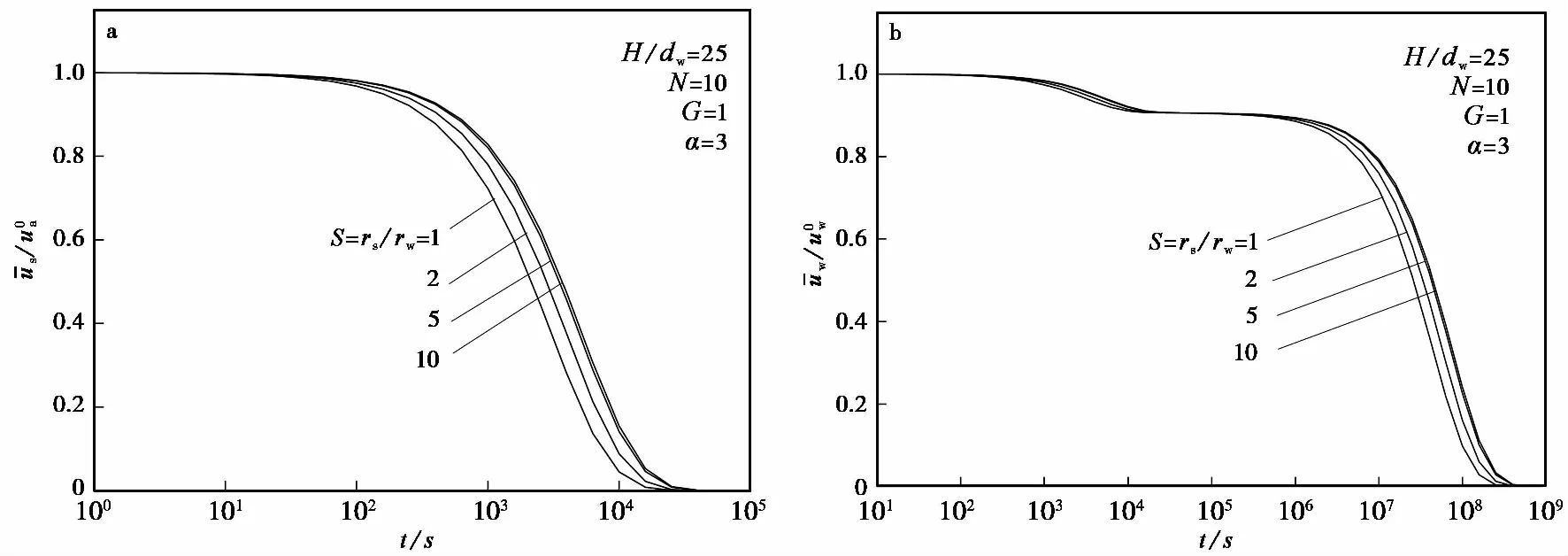
图与在不同α时的消散曲线Fig.5 Dissipation curves of different α

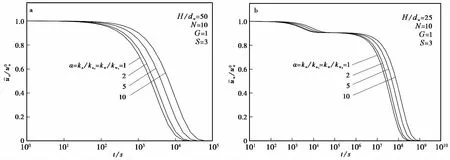
图与在不同S时的消散曲线Fig.6 Dissipation curves of different S

3 结 论

本文推导出了瞬时荷载下同时考虑井阻和涂抹作用的非饱和土竖井地基等应变固结解析解，并运用算例进行了参数影响分析，结论如下：

(1)将本文所得解退化至饱和土中，与饱和土竖井地基等应变固结的解析解对比，两者公式相同，验证了本文解的正确性。

(2)G、N越小，非饱和土竖井地基的固结速度越快；当G小于0.1时，建议实际工程中不考虑井阻作用。

(3)α、S越小，即涂抹作用越小，非饱和土竖井地基的固结速度越快；当S大于5后，涂抹作用对竖井地基固结的影响与S=5时无明显差异。

综上所述，井阻和涂抹作用对竖井地基固结均有明显影响，实际工程中建议尽量减少施工扰动并提高竖井的透水能力，以降低涂抹及井阻作用对非饱和土竖井地基固结的影响。

附录A参数说明

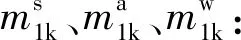
M：平均气体摩尔质量(kg/mol)；

R：气体常数(8.314J·(mol·K)-1)；

T：绝对温度(K)；

Sr0：初始饱和度；

n0：初始孔隙率；

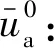
de、dw：影响区、竖井直径(m)；

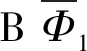
引入任意常数q1、q2，综合式(12a)、式(12b)得：

(B1)

通过变量Φ=uaq1+uwq2引入常数Q，式(B1)可被转化为如下方程组：

Qq1=Aaq1+Waq2

(B2a)

Qq2=Awq1+Wwq2

(B2b)

另外，式(B2a)与式(B2b)成立的条件为：

(Aa-Q)(Ww-Q)-AwWa=0

(B3)

因此，二次方程组(B3)的根Q1、Q2可以表示为：

(B4)

当Q=Q1时，式(B2a)、式(B2b)中的q1、q2分别为q11和q21。当Q=Q2时，q1、q2分别为q12和q22。

综上，式(B1)可以表示为以下的方程组：

(B5)

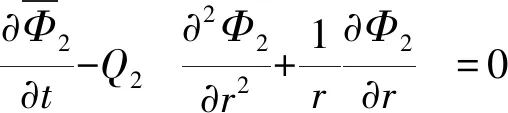
(B6)

式中：q12=(Q2-Ww)/Aw；q21=(Q1-Aa)/Wa。