小样本岩土参数下土质边坡可靠度分析的条件概率法*

蒋良潍 赵 晶 罗 强 张文生③ 熊卫平 孔德惠

(①西南交通大学，土木工程学院，成都 610031，中国)(②高速铁路线路工程教育部重点实验室，成都 610031，中国)(③新加坡国立大学，土木与环境工程系，新加坡 117576，新加坡)

0 引 言

作为岩土工程的重要分支，边坡稳定性分析一直备受关注(介玉新等，2017；叶帅华等，2018；苏永华等，2019)。边坡稳定性评价中，传统的安全系数法将岩土参数作为定值，并取大于1的经验性稳定安全系数来应对各类不确定性的综合影响，难以客观地表征边坡安全性。自20世纪70年代始，更严密的可靠度分析方法被引入到边坡工程中(Wu et al.，1970；杨继红等，2007；郑亚楠等，2014；王飞等，2016)，这类方法基于概率统计及随机过程理论，采用随机变量描述不确定性因素的概率特征，以可靠指标β或破坏概率Pf度量边坡的安全程度。

边坡可靠度分析中，对基本变量及计算模型等均考虑不确定性，根据其来源主要可归为物理不确定性、模型不确定性和统计不确定性三方面(祝玉学，1993)。其中，物理不确定性反映岩土物理力学指标的固有离散性及土工参数间的相互影响；模型不确定性来源于边坡稳定分析模型中对力学计算和边界条件的简化；而统计不确定性主要由于样本数量有限引起，体现为样本统计值随不同抽样批次而变化，在小样本条件下此类问题更为突出。

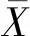
但相对而言，岩土体的物理不确定性较大(Wu et al.，1970)，且土工参数多由小样本勘察统计获得，样本估计值会对总体参数有所偏离，呈现“信息不完备性”的随机误差影响。若仍采用将样本估计值直接代入到可靠度分析(文中简称“直接代入法”)，则参数估计环节的随机误差将向后续的可靠度计算环节传递，分析结果相应会出现围绕可靠度真值随机偏离的不确定性现象。

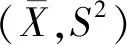
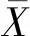
1 可靠度分析条件概率法

1.1 统计不确定性对岩土可靠度分析结果的影响

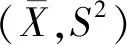
适当增加勘察取样数目即样本容量n，是减小统计不确定性的常用途径。从控制可靠度计算结果离散性角度，Babu et al.(2003)与谭晓慧等(2008)分别基于岩土参数正态分布假设，根据参数的物理变异性水平，分析了不同样本数目对滑坡破坏概率或可靠指标的影响；吴振君等(2013)与赵晶等(2016)采用不同取样数目进行计算机随机抽样来模拟获取勘查取样试验数据，分别讨论了软土和普通土边坡的合理样本数目取值。

但工程实际中限于条件或经济性，勘察资料仍多属于小样本数据(勘察取样数目最低甚至仅为n=6)，在这种“信息不完备”既有条件下，尽可能改善可靠度计算结果的可信度，有助于岩土工程可靠度分析的进一步应用。

1.2 基于条件概率原理的可靠度分析改进方法

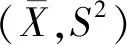
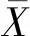
(1)

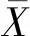
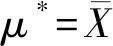
图1 有限样本估计总体均值的偏差及其发生概率Fig.1 Error and occurrence probability for the estimation of population mean based on limited samples

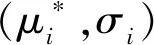
(2)

式中：P(·)为事件的发生概率；A为边坡失稳事件；Bi为μ*的不同取值事件。

具体计算中，须对连续型的概率密度曲线g(T)作离散化处理。根据偏差d的大小，将g(T)划分为多个毗邻子区间，g(T)曲线在各子区间内所围面积即估计偏差d的发生概率P(Bi)，其表示取不同假想总体的发生概率。对应地，设假想总体的参数取值共有m种可能性，将g(T)离散化为m个毗邻区间，破坏概率P(A)即可按全概率式(2)进行加权求和。

条件概率法的逻辑结构及与传统“直接代入法”(将样本估计值直接代入可靠度分析)的对比见图2。

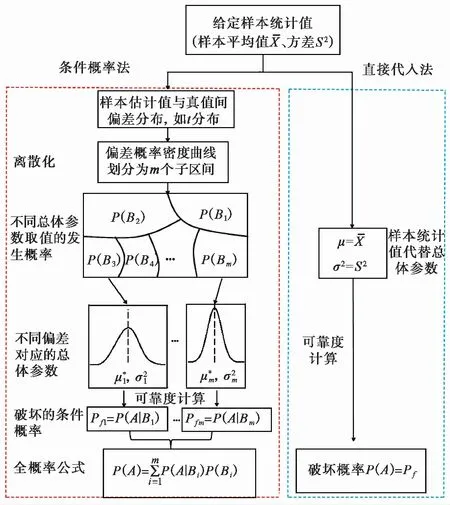
图2 条件概率法流程图Fig.2 Flow chart of conditional probability method

1.3 可靠度条件概率法计算流程

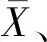
1.3.1 样本平均值与方差计算

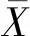
1.3.2 总体参数取值发生概率P(Bi)计算

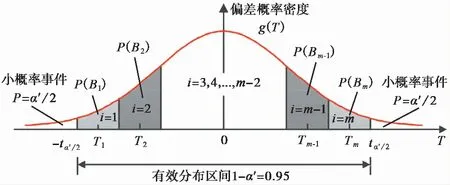
图3 估计偏差的概率密度函数子区间划分Fig.3 Subinterval division of the probability density function of estimation error

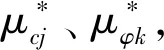
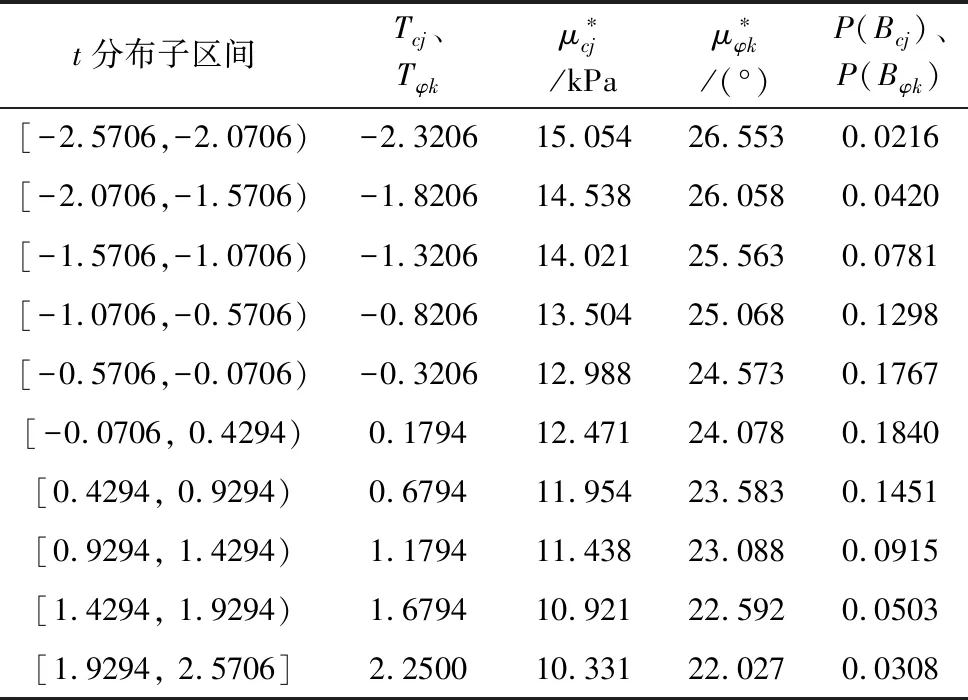
表1 t分布子区间划分Table 1 Subinterval division of the t distribution

1.3.3 基于全概率公式的边坡破坏概率P(A)计算

由c、φ相互独立，事件Bcj、Bφk同时发生(即事件BcjBφk发生)的可能性共有m1×m2种，事件BcjBφk的取值发生概率P(BcjBφk)=P(Bcj)·P(Bφk)。此时，采用事件BcjBφk对应的总体参数(μcj，σcj)、(μφk，σφk)计算得到的边坡失效概率P(A|BcjBφk)，即为事件BcjBφk下的条件概率。基于式(2)，c、φ双独立变量参数条件下，边坡破坏概率P(A)由式(3)计算。

(3)

式中：Bcj、Bφk为c、φ各自取不同总体均值事件。

2 条件概率法算例分析

2.1 样本随机抽样模拟及可靠度结果空间构建

通过勘探取样获取强度指标可看作从总体中随机抽取样本。为验证条件概率法对减小可靠度计算结果不确定性的效果，采用计算机随机抽样模拟法(吴振君等，2013；赵晶等，2016)进行给定样本数目的分批抽样，得到不同抽样批次下的样本值，通过充足批次抽样及相应可靠度计算，构建计算结果空间，对比条件概率法和传统直接代入法所得结果空间数据点的离散分布特征。

2) 根据所提出的循环迭代算法及通过三维扫描仪对复杂腔体表面进行反求建模实验研究，获得与零件表面相一致的三维实体模型，其效率大大高于三坐标测量仪，并可以对原产品的破损处进行修复、提取需加工的三维曲面模型。

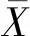
为考察两种方法计算结果与可靠度真值的偏离程度，重复上述抽样-计算过程N次，即为N批次抽样计算，两种算法分别得到各N个可靠度结果数据点即构建出各自的结果分布空间。当N足够大，结果空间中的数据散点反映了样本数目n条件下，可靠度结果的所有可能分布。显然，散点越向真值会聚，任一次抽样下的计算结果越有可信度，反映出越高的算法精准度。其中，可靠指标真值β0由总体参数(μ，σ2)计算得到，其只反映物理不确定性影响，排除了统计不确定性问题，可作为衡量小样本条件下算法效果的基准。

需要指出的是，采用Monte Carlo模拟方法直接得到的是边坡失效概率Pf。在工程实践中，由Pf转换得到的可靠指标β更加便于应用，两者之间存在换算等式Pf=Φ(-β)，其中Φ(-β)为标准正态分布的累计概率函数(Phoon，2008)。文中采用可靠指标进行对比。

2.2 边坡可靠度计算模型及参数总体

以简单均质土坡(如路堤边坡)为对象开展对比，研究条件概率法在可靠度分析中的效果。边坡坡高H=8m，地基厚度D=10m，坡率1︰1.5，如图4所示，边坡稳定性分析方法选用极限平衡Fellenius法。

图4 简单土坡模型(单位：m)Fig.4 Model of simple soil slope(unit：m)

设边坡土体强度参数c、φ服从相互独立的正态分布，c、φ总体均值取10kPa、21.71°，变异系数分别取0.3、0.2(骆飞等，2017)，对应c、φ总体的标准差为3kPa、4.34°。由于土体重度变异性一般较小，取定值γ=20kN·m-3，计算得到边坡可靠指标真值β0=1.15。

2.3 可靠度计算结果及分析

取工程勘察实际中对样本容量规定的下限n=6开展计算分析，此时统计不确定性影响也最为显著。根据c、φ总体均值和方差，利用MATLAB软件的normrnd函数生成各含5000组元素的c、φ正态总体，基于“3σ准则”(张继周等，2008)剔除极小概率异常数据后，经Kolmogorov-Smirnov分布拟合检验(祝玉学，1993)证实c、φ总体的正态分布性质。

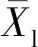
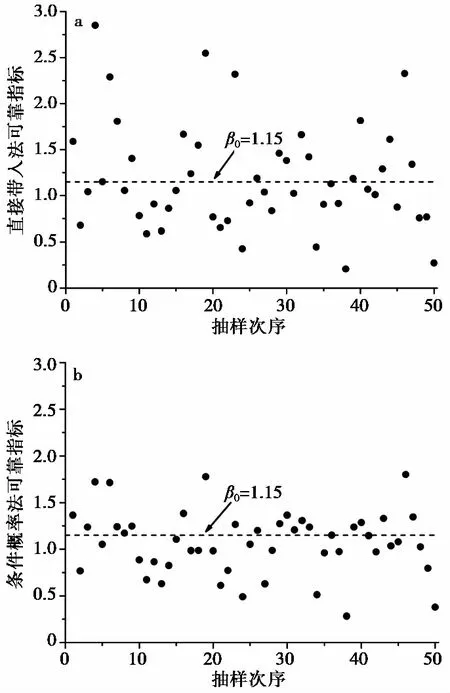
图5 可靠指标散点图Fig.5 Scatter of reliability indicesa.直接代入法；b.条件概率法

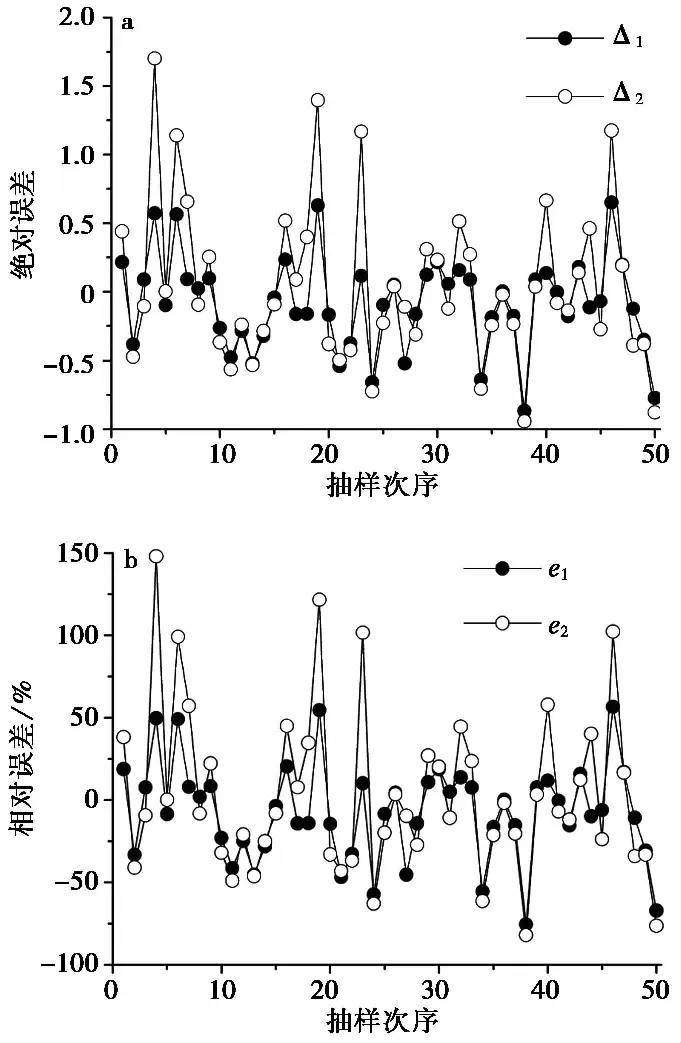
图6 可靠指标的绝对误差与相对误差Fig.6 Absolute error and relative error of reliability indicesa.绝对误差；b.相对误差

将两种方法的可靠指标相对误差的差值(e2-e1)绘制频率直方图，如图7所示，图中横坐标的正值表示直接代入法的相对误差大于条件概率法，负值则反之。可以看出，约80%的绝大部分情况下，条件概率法的相对误差较直接代入法更小。其中，55%占比情况，相对误差减小约20%；25%占比情况，相对误差减小20%～90%。而条件概率法的相对误差略大于直接代入法的情况较少，仅占结果总数的约20%，相对误差也最多不超过20%。

图7 两种方法可靠指标相对误差直方图Fig.7 Relative error histogram of the reliability indices from two methods

算例表明，小样本条件下，直接代入法所得结果离散性较大，更易造成可靠度计算结果的不确定性。比较而言，条件概率法的结果更趋近可靠指标真实值β0，数据散点围绕真实值更为会聚，表明其结果可信度更高。

特别的是，在抽样发生较大参数估计偏差情况下，条件概率法可明显提高分析结果准确性。如第4#、6#、7#、19#、23#和46#批次抽样的误差较大，而对比两种方法的可靠指标结果(表2)可见，直接代入法的可靠指标与真值(β0=1.15)相差较大，而条件概率法将可靠指标绝对误差减小0.53～1.13，收敛控制效果显著(达到一至两个可靠度级别)，相对误差亦减小46.09%～98.27%。因此，条件概率法避免了参数估计出现偶然性较大误差所致的计算波动。

表2 发生较大抽样偏差时两种方法可靠度分析结果对比Table 2 Comparison of the reliability analysis results under large sampling bias

3 条件概率法的相关讨论

3.1 子区间划分数目的敏感性分析

文中第1.3节在考虑了计算量与计算精度后采用了m1=m2=10的子区间划分数目。为讨论子区间划分数目对条件概率法可靠指标β1的影响，以第2.2节边坡可靠指标真值β0=1.15对应的强度参数组合为例(c、φ总体均值取10kPa、21.71°，总体的标准差为3kPa、4.34°，重度γ=20kN·m-3)，依次取m1=m2=[6，8，10，14，18，22]，计算对t分布密度曲线进行不同子区间数目划分下的边坡稳定可靠指标值，结果如图8所示。

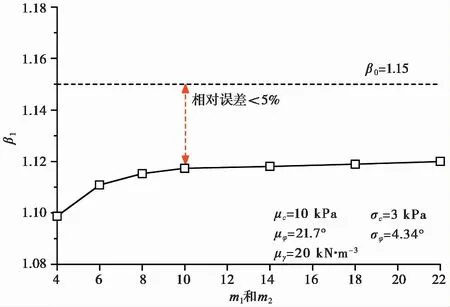
图8 子区间划分数目敏感性分析Fig.8 Sensitivity analysis of subinterval numbers

观察图8可知，条件概率法的可靠指标计算结果对子区间划分数目的敏感性随m1和m2增大而降低。划分数目越多，构造的假想总体越完备，条件概率法结果越靠近真值(渐近线)。而当子区间划分数目超过10，与真值β0的相对误差不大于5%。因此，在保证分析结果精度的前提下为降低计算量，取10作为t分布概率密度函数划分段数具有合理性。

3.2 条件概率法扩展应用讨论

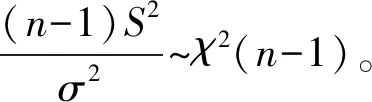
此外，文中在介绍条件概率法原理时，对土体强度参数c、φ采用了常用的相互独立正态分布假设。对于强度参数总体服从其他分布的情形，若满足下列两个条件之一，条件概率法仍适用：(1)参数总体所服从的分布函数与正态分布间可进行正、逆转换。如对数正态分布与正态分布之间的对应转换；(2)所服从分布的矩估计偏差分布具有明确的概率表达式。如正态分布总体下以样本平均值估计总体均值所产生偏差的概率关系以t分布表达，非正态分布下，t分布应替换为相应分布。

4 结 论

针对小样本岩土参数统计不确定性对可靠度计算的影响，研究提出了小样本参数下土质边坡可靠度条件概率计算方法；以简单均质土坡为对象开展充足批次的小样本抽样与可靠度计算，对比了条件概率法与传统直接代入法计算结果的误差与数据分布离散性，验证了条件概率法对减小可靠度计算结果不确定性的效果。主要结论如下。

(1)基于样本平均值与总体均值的估计偏差服从t分布的概率特征，构造不同偏差量所对应的假想总体并确定其发生概率，根据条件概率原理分析抽样偏差对计算结果的权值影响，通过Bayes公式建立了小样本下土质边坡可靠度计算的条件概率法，并给出了详细计算流程。

(2)简单土坡算例表明，较之传统的直接代入法，条件概率法在约80%绝大部分情况下得到了更趋近于真值的可靠度分析结果，可靠指标的数据分布离散性更小，表明结果的可信度更高，在参数抽样发生较大偏差情况下体现了更为显著的效果。仅20%占比的情况，条件概率法结果较直接代入法稍偏离真值，但差异不明显。