四面楔形体监测敏感部位试验研究*

晏长根 安 宁 薛志佳 杜 柯 许江波 孙巍锋

(①长安大学公路学院，西安 710064，中国)(②陕西宝汉高速公路建设管理有限公司汉川分公司，汉中 723000，中国)

0 引 言

岩土工程中边坡安全问题十分突出(刘传正，2019；叶唐进等，2019)，其中楔形体破坏是一种较为常见的岩质边坡破坏类型。楔形体一般由边坡上两个或两个以上的结构面分割而成，结构和力学机制较为复杂(陈祖煜等，2005)，严重威胁人民生命财产安全(邓辉等，1999；许强等，2009)，因此对于楔形体的监测预警研究十分必要。

目前关于楔形体的研究主要集中在对其稳定性的分析，研究方法包括极限平衡法(Hoek et al.，1981；唐红梅等，2015)、塑性极限分析上限解法(Chen et al.，1999)、广义极限平衡法(Wang et al.，2004)、塑性力学广义解法(Chen，2004；Li et al.，2013)、塑性极限分析下限法(Liang et al.，2014；Zhou et al.，2017)、可靠度理论分析(Jimenez Rodriguez et al.，2007；Wang et al.，2018)、人工神经网络分析(Jiang et al.，2013)、概率分析法(Zheng et al.，2016；秦胜伍等，2017;Ma et al.，2019)以及分析楔形体动力稳定性的动力矢量法(Ni et al.，2014)等，这些研究方法对楔形体稳定性分析的研究起到了巨大的促进作用，但这些研究工作多集中在分析方法方面，对于较为准确地反映楔形体破坏时其结构面处内部位移及内部应力变化情况和确定楔形体的监测方法存在局限。

监测是研究边坡的一种重要手段，传统的边坡监测方法主要为位移监测(董文文等，2016)。范永波等(2013)对某矿山滑坡进行地表和深部位移监测，结合现场地质条件调查，研究了滑坡发生的地质成因和环境成因，分析了位移监测结果，为滑坡的深部位移监测深度确定提供一定的借鉴和参考。何建友等(2007)采用孔内水平位移监测手段与探井编录相结合的方法，确定了某公路滑坡的滑动面位置、滑动面位移、滑动方位及滑动速率等滑动面参数，为滑坡治理设计提供了量化的工程地质依据。丁瑜等(2011)对某厂房后坡进行了深部位移监测，并根据监测结果对滑坡体的范围、整体活动性、滑动方向、滑动面以及滑坡类型进行了分析。然而有研究表明只有在临近破坏时，边坡才会出现较为明显的变形，此时基于位移监测的预警响应较为迟缓(何满潮，2009；郭永建等，2013)。锚杆是楔形体加固的一种常用手段(李泽等，2016)，基于锚杆的应力监测受到部分学者的关注和探讨。郭永建等(2013)利用强度折减法分析了支护锚杆的轴力随岩体强度降低过程的变化规律，并确定应力监测预警值。张院生等(2015)基于锚杆监测构建了矿山边坡无线预应力锚杆监测系统，并对监测预警值的确定进行了探讨。刘祖强等(2004)基于监测锚杆应力测值的多元回归分析结果，对边坡的稳定性状态进行了评价。

目前基于现场监测所获得的边坡破坏全过程的监测资料较少(董秀军等，2015)，且研究过程耗时长、耗资大，而通过模型试验的方法可较好地解决这一问题。晏长根等(2017，2018)开展均质岩质边坡离心模型试验，分析了锚杆的应力响应规律，结合数值方法探讨了均质岩质边坡单锚应力监测的较佳位置，并提出了基于锚杆监测的单滑动面边坡动态预警分析及安全分级方法。郭永建等(2016)结合岩质边坡离心模型试验，认为采用锚杆应力监测的方法评价公路岩质边坡的稳定性具有可行性。董秀军等(2015)开展边坡物理模拟试验，获取了不同受力条件下斜坡变形破坏的时间-位移曲线簇。Zhang et al.(2020)通过模型试验方法对楔形体在滑动失稳过程中滑动面处地下水动态演化规律进行了探讨，并结合试验结果对楔形体稳定性进行了分析。

可以看出，目前针对楔形体的研究主要是通过力学分析手段对其稳定性进行评价，在一定程度上忽视了楔形体在破坏过程中结构面处内部位移和内部应力的变化趋势，有关楔形体监测敏感部位的研究也鲜有报道。本文利用物理模拟试验方法，对岩质四面楔形体在结构面抗剪强度降低条件下的结构面处内部位移和内部应力进行了监测和分析，确定了楔形体在滑动失稳过程中结构面处的位移和应力监测敏感部位，为岩质边坡楔形体的安全监测提供了参考依据。

1 试验方案

1.1 试验装置

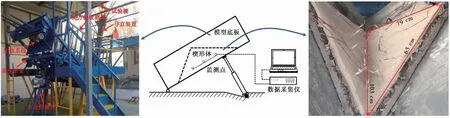
图1 试验装置及模型示意图Fig.1 Diagram of test device and wedge model

1.2 试验材料及模型尺寸

本次试验对象为均质岩石边坡中的楔形块体。岩体模型按照重晶石粉∶砂∶水泥∶水=3︰4.2︰1.8︰1的比列配制，其物理力学参数如表1所示。

表1 岩体模型材料基本参数Table 1 Parameters of rock mass model materials

楔形体结构面以滑石粉、细砂、石膏、黄土和水按照4︰3︰1︰1︰1的比例配制。配制完成的结构面材料的弹性模量为25.2MPa，黏聚力为0.9 ikPa，内摩擦角为25°。

模型试验平台的底板能够沿中轴实现横向对折，形成0°～180°夹角的两个相交结构面，故直接以对折成一定夹角的两个平台底板面为楔形体结构面底层岩体来构筑楔形体模型。底层岩体的厚度控制为5cm，并采用预制的办法浇筑，结构面的铺设厚度为1.5cm。由于楔形体模型的体积较大，故分层浇筑，分层面处做凿毛处理。楔形体模型示意图如图1所示。

本次试验中两模型结构面与竖直平面的夹角均为45°；楔形体结构面交线与坡面夹角为40°，与坡顶面夹角为30°；楔形体结构面交线的长度为103cm，两结构面的三边尺寸均为103cm、79cm、65cm，浇筑成型的结构面如图1所示。

1.3 试验量测装置布置

本次试验的量测内容为楔形体结构面处的内部位移和内部应力。

结构面处内部位移采用自制的线拉式位移计量测，如图2所示。该线拉式内部位移计主要由百分表、百分表支架、直径0.6mm钢丝、直径1.5mm毛细不锈钢管和长度为2cm的20×20角钢组合而成。其中角钢浇筑在楔形体底部，毛细钢管固定在结构面上，钢丝的两端分别与角钢和百分表测量杆相连，楔形体滑动时带动各位移测点处的角钢滑动，进而通过钢丝拉动百分表的测量杆，从而通过读取百分表读数来获得结构面处各位移测点的位移值。

图2 线拉式内部位移计Fig.2 Line-pull internal displacement meter

结构面处内部应力采用箔式电阻应变片量测。借鉴锚杆应力测试原理，试验时在一段镁铝合金条上粘贴应变片，将镁条的一端锚固在结构面模型下层岩体内，另一端锚固在楔形体模型内，镁铝合金条的横截面尺寸为10mm×1mm，弹性模量为4.5×104iMPa。由于基层岩体为预制的，且其材料强度并不高，因此在将基层岩体置于模型试验平台预定位置后，在基层岩体上凿出用于锚固镁条的小孔，将镁条的一端采用胶水锚固在小孔内，并确保应变片恰好位于基层岩体外部，之后再逐一浇筑结构面材料和楔形体材料，为使镁条另一端能够牢固地锚固于楔形体模型内，浇筑时将镁条末端弯折，应变片的安装示意(图3)。此外为避免测量线缆过于集中而影响结构面的材料性质，因此各监测点处的测量导线均沿垂直于结构面交线方向引出，同时将导线埋设于结构面内靠近底层岩体处。

图3 应变片布设示意图Fig.3 Diagram of strain gauge arrangement

线拉式位移计受力端头均匀浇筑在两个结构面上与结构面交线平行且间距15cm的两条直线l1和l2位置处以及结构面交线l位置处，如图4a所示，监测点编号为D1～D9。

图4 楔形体结构面监测点布设图Fig.4 Layout of monitoring points for wedge structural surfacea.位移监测点；b.应力监测点

结构面上的内部应力监测点临近位移监测点，如图4b所示，沿直线l1、l2和l分别均匀布设4个应力监测点，编号为S1～S12。

1.4 试验方法

根据试验任务，如何使楔形体沿结构面产生滑动是试验能够进行的关键。本次试验通过提高结构面材料含水率来降低其抗剪强度，从而使楔形体沿结构面产生滑动失稳，具体方法是将管身均布有出水孔的塑料细管沿平行于结构面交线方向预埋在结构面中，各塑料细管的间距为6cm。塑料细管的下端封堵，上端露出，试验时利用注水器通过上部端口向管内注水。

模型养护完成后，通过试验平台控制装置，调整平台底板主倾角为35°，待楔形体静置12h后，利用注水器向塑料管进行第一次注水，同时对结构面处内部位移和内部应力的数据进行采集。当楔形体结构面处所有位移监测点的监测位移量均不超过每小时0.05mm时，开始进行下一次注水工作，每次的注水量为100mL，并按照10mL·min-1的注水速率缓慢注水。当楔形体结构面处的累计位移量达到5mm时，便认为楔形体已发生失稳。

2 试验结果与分析

2.1 位移监测结果及分析

2.1.1 位移过程线比较

图5为整个试验过程中结构面处内部累计位移随时间的变化曲线。本次试验共注水4次，从开始试验到楔形体发生失稳破坏历时690min。可以看出，在楔形体失稳破坏之前，每一注水阶段内，各监测点位移过程线都呈现出先缓慢增长后迅速增长再趋于平直的形态。这是由于每次注水完成后，水还未在结构面模型材料内完全扩散，没有均匀降低结构面的抗剪强度，故位移随时间的变化曲线呈现出缓慢增长的形态；伴随着水分在结构面的扩散，结构面整体抗剪强度也随之降低，监测点位移量也因此迅速地增长；水分在结构面材料中扩散的同时也会向基层岩体和楔形体中渗透，结构面材料的含水率会随之降低，因此其抗剪强度有所恢复，楔形体最终趋于自稳平衡，此时各位移监测点处位移量随时间的变化曲线呈现出平直的变化趋势。在最后一次注水完成后，位移过程线出现明显的拐点，曲线斜率明显增加，各监测点处的位移量迅速增长直至楔形体失稳破坏。

整个试验过程中，各监测点处位移表现为D3>D2>D1、D6>D5>D4、D9>D8>D7。试验结束时，D6监测点的位移量为最大值，即D6>(D3、D9)，为5.15mm；而最小位移发生在D4监测点，即D4<(D1、D7)，为4.45mm。

图5 累计位移量随时间的变化曲线Fig.5 Curve of cumulative displacement with time

2.1.2 位移变化平均速率比较

试验过程中各个注水阶段内位移变化平均速率如图6所示。可以看出，后一注水阶段内的位移变化平均速率均较前一注水阶段内有所提升。最后一次注水后，位移变化平均速率的提升尤为明显，这与位移过程线在最后一次注水完成后出现拐点的现象相吻合。

图6 每一注水阶段内位移变化平均速率Fig.6 Average rate of displacement change in each water injection stage

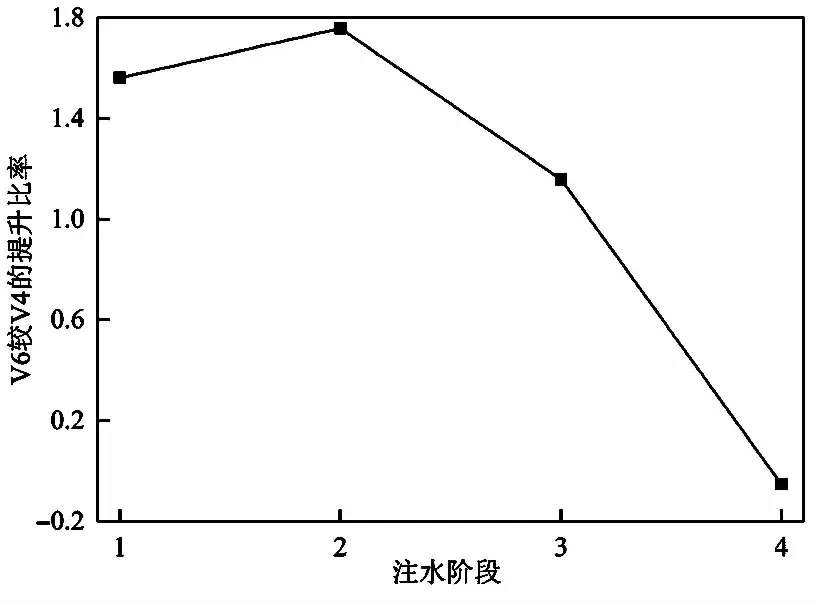
在前3次注水阶段内，各个监测点处的位移变化平均速率有：V3>V2>V1、V6>V5>V4、V9>V8>V7，且V6为最大值，V4为最小值。而在最后一次注水阶段内，各监测点处的位移变化平均速率有：V3

图7 每一注水阶段内V6较V4的提升比率Fig.7 The improvement ratio of V6 to V4 in each water injection stage

图8为试验全过程中各监测点位移变化平均速率图。可以看出，各监测点处的位移变化平均速率有：V3>V2>V1、V6>V5>V4、V9>V8>V7；其中V6为最大值，V4为最小值，V6较V4的提升比率为15.76%。

图8 试验全过程各监测点位移变化平均速率Fig.8 Average rate of displacement change of each monitoring point in the whole test process

2.2 应力监测结果及分析

2.2.1 应力监测曲线比较

试验中通过应变片监测得到各测点的应变值，进而通过式(1)计算得出各监测点处的应力值。

σ=Eε

(1)

式中：σ为各应力监测点处的应力值；ε为各应力监测点处监测得到的应变值；E为镁铝合金条的弹性模量。

图9为整个试验过程中各应力监测点的应力监测曲线。与位移监测曲线相似，在每一注水阶段内，应力监测曲线也呈现出先缓慢增长后迅速增长再趋于平直的变化趋势，但位移监测曲线的这种变化趋势更明显。在最后一次注水完成后，应力监测曲线也出现拐点。

图9 应力随时间的变化曲线Fig.9 Curve of stress with time

整个试验过程中，各监测点处内部应力表现为S4>S3>S2>S1、S8>S7>S5>S6、S12>S11>S10>S9。楔形体破坏时，S8监测点的应力值为最大值，为1.210MPa；而最小应力发生在S6监测点，为0.839MPa。

图10 试验过程中各监测点处监测值与最终监测值的比值Fig.10 Ratio of the monitored value at each monitoring point to the final monitored value during the test

图11为试验过程中各监测点处监测值与最终监测值的比值，以S4、S8和S12应力监测点以及D3、D6和D9位移监测点的监测值为例，可以看出，整个试验过程中应力监测值所对应曲线均位于位移监测值所对应曲线上部，且应力监测值所对应曲线呈现出近似线性的增长趋势，而位移监测值所对应曲线在560min后才出现明显的增长趋势，此时已接近楔形体产生失稳破坏。当位移监测值/总位移值为0.5时，位移监测值对应曲线所用时间为620min，而当应力监测值/总应力值为0.5时，应力监测值对应曲线所用时间为430min，明显低于位移监测值对应曲线所用时间，因此可以认为应力监测较位移监测的反馈更为提前，能够更及时地对边坡变化产生响应。

图11 每一注水阶段内应力变化平均速率Fig.11 Average rate of stress change in each water injection stage

2.2.2 应力变化平均速率比较

图11为各监测点在每一注水阶段内的应力变化平均速率图。在前3次注水阶段内，各监测点处的应力变化平均速率均有：V4>V3>V2>V1、V8>V7>V5>V6、V12>V11>V10>V9，且V8为最大值。在最后一次注水阶段内，各监测点处的应力变化平均速率均有：V1>V2>V3>V4、V6>V5>V7>V8、V9>V10>V11>V12，且V6为最大值。S4、S8、S12监测点均位于楔形体下部，说明在失稳过程前期，楔形体下部为应力监测敏感部位；而S1、S5、S6、S9位于楔形体中部偏上位置，说明在临近失稳时，楔形体中上部为应力监测敏感部位。本试验中，楔形体失稳过程前期，S8监测点为应力监测最敏感点；而在临近楔形体失稳时，S6监测点为应力监测最敏感点。

3 工程应用探讨

采用监测手段及时对楔形体的滑动失稳做出预警可以有效降低其危害程度。本文通过开展岩质边坡四面楔形体物理模拟试验，发现在楔形体滑动失稳前期，位移监测和应力监测敏感部位均在楔形体下部；而临近楔形体失稳时，楔形体中上部为位移监测和应力监测敏感部位，且应力监测相比位移监测的反馈更为提前。在实际工程中，将位移监测传感器布置在楔形体结构面存在一定的困难，但是可以利用锚杆监测的手段对结构面处的内部应力进行监测，因此本文建议在对楔形体进行监测时，可采用锚杆应力监测的方式重点监控楔形体上部和下部结构面处的应力变化，从而及时地对楔形体失稳发出预警，并降低监测成本。

4 结 论

(1)随着楔形体滑动位移的增加，各位移监测点处位移变化速率的差异性越小，楔形体表现出的整体滑动特性更为明显。

(2)在楔形体失稳过程前期，沿结构面交线向下，内部位移变化速率越大，对位移的变化较为敏感；临近破坏时，沿结构面交线向上，内部位移变化速率越大，对位移的变化更为敏感。就本试验而言，楔形体失稳过程前期，结构面交线最下部D6监测点为位移监测最敏感点，而临近失稳破坏时，结构面交线最上部D4监测点为位移监测最敏感点。

(3)在楔形体失稳过程前期，楔形体下部为应力监测敏感部位；临近失稳破坏时，楔形体中上部为应力监测敏感部位。本试验中，楔形体失稳过程前期，结构面交线最下部S8监测点为应力监测最敏感点；而在临近楔形体失稳破坏时，结构面交线中上部S6监测点为应力监测最敏感点。

(4)应力监测相比于位移监测的反馈更为提前，能够更及时地对边坡变化产生响应。