对比拓展 让复习课更高效生动——“椭圆中的定点问题”复习课教学重现

梁修曦

(湖北省十堰市郧阳中学 442000)

一、课堂再现

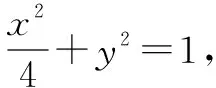
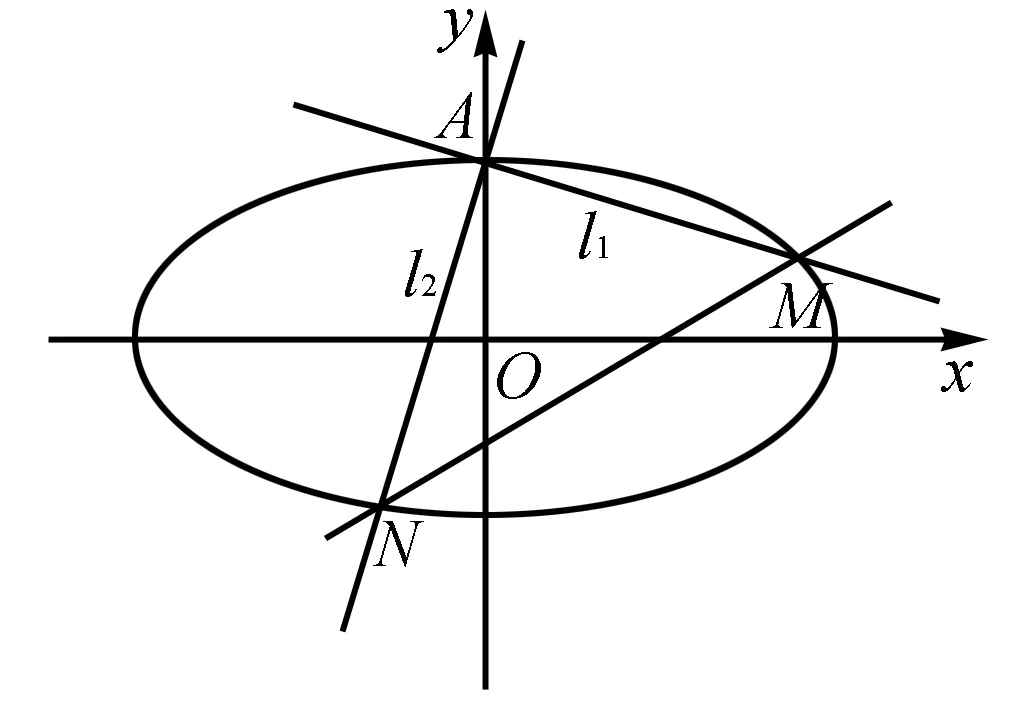
图1

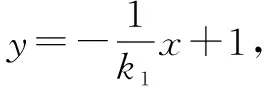
生2：也可直接设MN的方程为y=kx+m，利用kAM·kAN=-1求得m与k的关系式，从而得到定点的坐标.

师：这两种思路都很好，请你们写出求解过程.

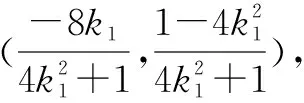
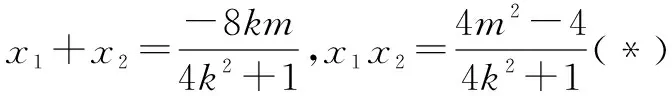
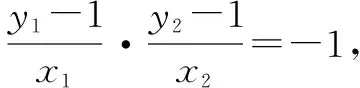
师：这两种方法均为证明直线恒过定点问题的通性通法. 比较来看，那种方法稍好一些呢？

生3：方法1思路简洁，依照题意直接计算即可.

生4：方法2目标明确，求哪条直线过定点，就设哪条直线方程为y=kx+m，再寻找m与k的关系式，计算都很常规.

生5：两种方法都差不多.

师：既然大家难以取舍，接下来我们看变式1，再次体验一下.

变式1在问题1中，将A点坐标改为(2，0)，其他条件和求证不变.

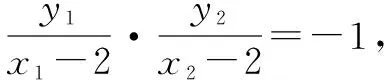
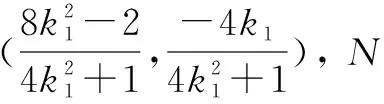
师：其他同学有什么办法解决这个问题吗？

师：回答正确，我们在解决定点问题中，有时要灵活运用图形的几何性质帮助我们的计算.再次对比，我们发现：方法1涉及到方程的化简，有时会比较复杂，而方法2的计算量就稍小一些，运用起来更方便.

生9：问题1还有更简单的解法！

师：好，请你给大家讲一讲.

生9：因为这里是两直线的斜率之积等于-1，我们可以联想到韦达定理.

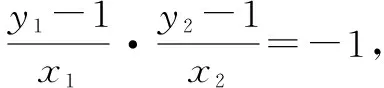
师：非常精彩！这是此类问题的一种巧解.联想到韦达定理，巧妙地将椭圆方程变形为以斜率为主元的二次方程，使计算量大幅减少，值得大家学习！

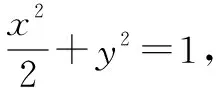
图2

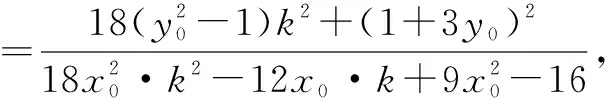
综上知，以MN为直径的圆恒过定点(0，1).

师：回答正确，这就是“找定点”问题的通性通法.其步骤是：先假设存在符合题目条件的点，再化图形特征为代数计算，看能否找到方程的解.最后再验证方程的解是否符合题目要求.其中会涉及到恒成立或代数式为定值的问题，需认真观察式子的结构，找到对应的办法.

最后，请大家再观察问题1和2，它们有什么联系？

生11：它们是对偶问题，问题1是已知以MN为直径的圆过定点，求直线过的定点；问题2是直线转动，求圆过的定点.

师：对，它们其实是同一个问题从两种不同角度设问.这类问题有一个一般性结论，大家下课后可以继续探究：

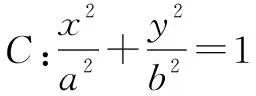
二、回顾与反思

在备本节复习课时，笔者的主要思路是设计一组关联题目，求解时能用到“证定点”和“找定点”两类问题的全部方法和技巧.问题1是一个“证定点”问题，解答中涵盖了动点坐标设题法和动直线方程设题法，为了比较两种方法的优劣，引入了变式1，同时也渗透了利用图形对称性辅助计算的技巧；利用韦定理巧解则是本节课的意外收获，体现了学生思维的灵活多变.问题2是一个“找定点”问题，它需要“先猜后证”，把动态几何特征变化转化为代数计算，进而找到定点.而对恒等式的处理，也是学生的弱项，需要学生具备良好的观察和分析能力.最后，通过对比，看清问题1和2的本质是同一个问题的两种不同角度设问，进而提炼总结出一般性的结论.

总之，定点问题在高中圆锥曲线教学中是热点问题，也是一个难点，它既考查学生的计算推理能力，更注重学生对动态问题的处理能力，锻炼学生熟练地将“数”的计算与“形”的分析结合起来.圆锥曲线章节的复习课更需要精心地设计问题，通过横向深挖纵向拓展，一方面可以减少部分重复的计算，直接进入核心的思维环节，又可以促进学生构建完整的知识网络，让课堂更高效生动.