力学中往返运动问题综述
杨晓丹
(重庆市第三十七中学校 400084)
在高中物理的复习和考试中,单个物体或多物体体系做往返运动的实例屡见不鲜.根据该类问题中研究物体的速度变化规律,我们把往返运动基本可分为:类上抛型(“v零v”型)、“零v零”型和“鹿回家”三大类型,下面将对这三种类型问题的运动规律以及求解思路等展开具体描述.
一、类上抛型(v零v型)
有这样一种往返运动,它虽然不是严格的竖直上抛运动,却可以采用类似的方法来处理;它的初末速度虽然不一定表现出严格的对称性,却也呈现出“非零—零—非零”的变化趋势,这类运动被统称为“类上抛”或“v零v”运动.表1总结了几种典型类上抛运动的运动规律和对应v-t图.

表1 典型类上抛模型的物理规律对比
例1 如图1甲,倾角为37°的足够长的传送带以恒定速度运行,将一质量m=1 kg的小物体以某一初速度放上传送带,物体相对地面的速度大小随时间变化的关系如图1乙所示,取沿传送带向上为正方向,g取10 m/s2,sin37°=0.6,cos37°=0.8.则下列说法正确的是( ).
A.物体与传送带间的动摩擦因数为0.75
B.0~8 s内因摩擦产生的热量为72 J
C.0~8 s内物体机械能的增量为84 J
D.0~8 s内因放上物体,传送带电动机多消耗的电能为216 J
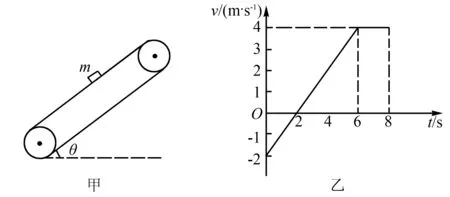
图1
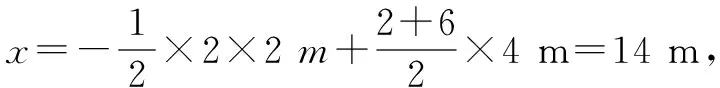
点评本题每个选项都要求学生找出对应物理过程并列式计算,比较繁琐.但若对“类上抛”型往返运动十分熟悉,通过本题给出的v-t图像,就不难联想到对应运动规律,进而提高做题速度.
例2 若在运动过程中空气阻力大小不变,竖直向上抛出物体的初速度大小与返回抛出点时速度大小的比值为k,物体返回抛出点时速度大小为v,重力加速度为g,则物体从抛出到返回抛出点所经历的时间为( ).
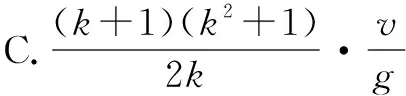
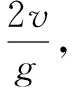
点评通过比较发现,由题设初速度为k·v,具体分析本题的运动过程,把时间硬算出来,不仅耗费大量时间,同时也给答题者的计算带来了负担.但在熟练掌握竖直上抛运动的运动规律之后,结合选项特点即可通过巧取特殊值完成快速求解.
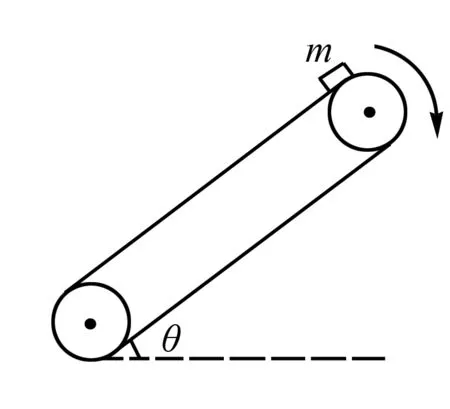
图2
例3 如图2所示,足够长的传送带与水平面夹角为θ,以大小为v0的速度顺时针匀速转动,在传送带的上端放置一个小木块,并使小木块以大小为2v0的初速度沿传送带向下运动,小木块与传送带间的动摩擦因数μ>tanθ,图3四幅图能客观地反映小木块的速度随时间变化关系的是(以木块的初速度方向为正方向)( ).
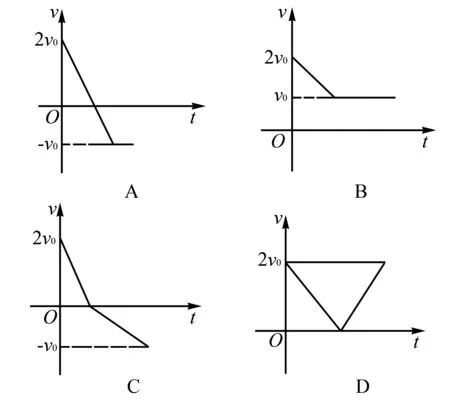
图3
解析小木块沿传送带向下运动的过程中所受的滑动摩擦力沿斜面向上,设小木块的质量为m、加速度大小为a,因为μ>tanθ,所以μmgcosθ>mgsinθ,故小木块做匀减速运动,根据牛顿第二定律得μmgcosθ-mgsinθ=ma,解得a=μgcosθ-gsinθ,当小木块的速度减小到零时,小木块相对传送带向下运动,其所受的滑动摩擦力沿斜面向上,小木块沿传送带向上做匀加速直线运动,根据牛顿第二定律得a=μgcosθ-gsinθ,当小木块的速度增加到v0时,小木块受沿斜面向上的静摩擦力,由于重力沿斜面方向的分力小于最大静摩擦力,故小木块与传送带保持相对静止,选项A正确,B、C、D错误.
点评本题部分学生会错用“粗糙斜面上或倾斜传送带上的往返问题”物理模型,以至于选择C选项.可见即使同为含传送带的类上抛问题,其运动规律还是略有不同的,不可一概而论.借助v-t图像仔细对比,做好辨析是关键.
二、“零v零”型
“零v零”型问题,顾名思义即表示在一定的坐标系下,研究对象的速度以零开始,以零结束的问题.这类问题的运动特征有:
①研究对象的运动状态和运动形式常表现出一定的规律性和周期性;
②研究对象的速度在从零变回到零的过程中,一定有最值存在.
“零v零”型问题中驱使研究对象完成速度变化的作用力可以是恒力,也可以是变力,前者范例十分常见,故本文不再赘述;后者在高中阶段是以轻绳、轻杆和轻弹簧这三种物理模型最为典型.值得一提的是,对于变力系统而言,求取速度最值的具体位置难以绕过超越方程的求解,有时甚至根本无法得到确定的解析解,只能获得数值解.
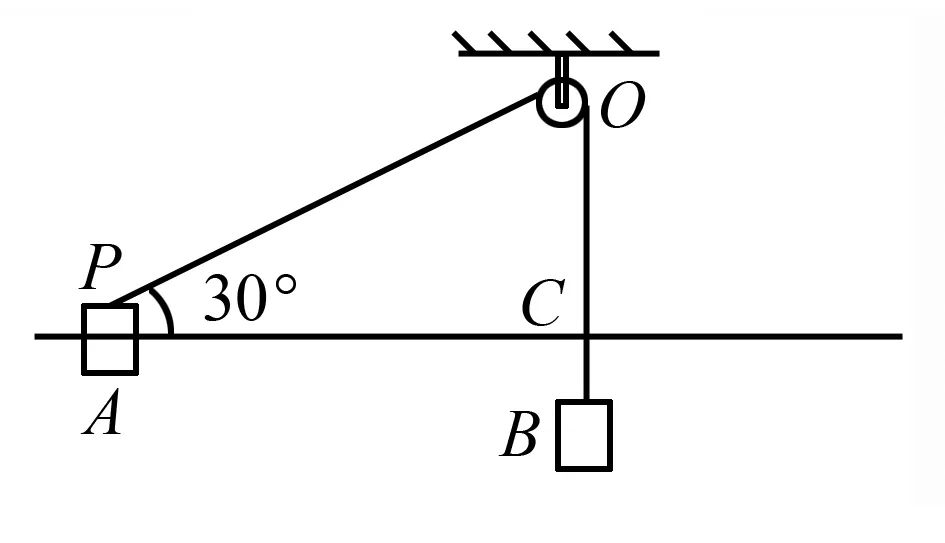
图4
例4 如图4所示,水平光滑长杆上套有一个质量为mA的小物块A,细线跨过O点的轻小光滑定滑轮一端连接A,另一端悬挂质量为mB的小物块B,C为O点正下方杆上一点,滑轮到杆的距离OC=h.开始时A位于P点,PO与水平方向的夹角为30°.现将A、B同时由静止释放,则下列分析正确的是( ).
A.物块B从释放到最低点的过程中,物块A的动能不断增大
B.物块A由P点出发第一次到达C点的过程中,物块B的机械能先增大后减小
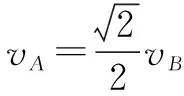
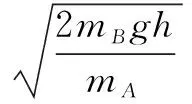
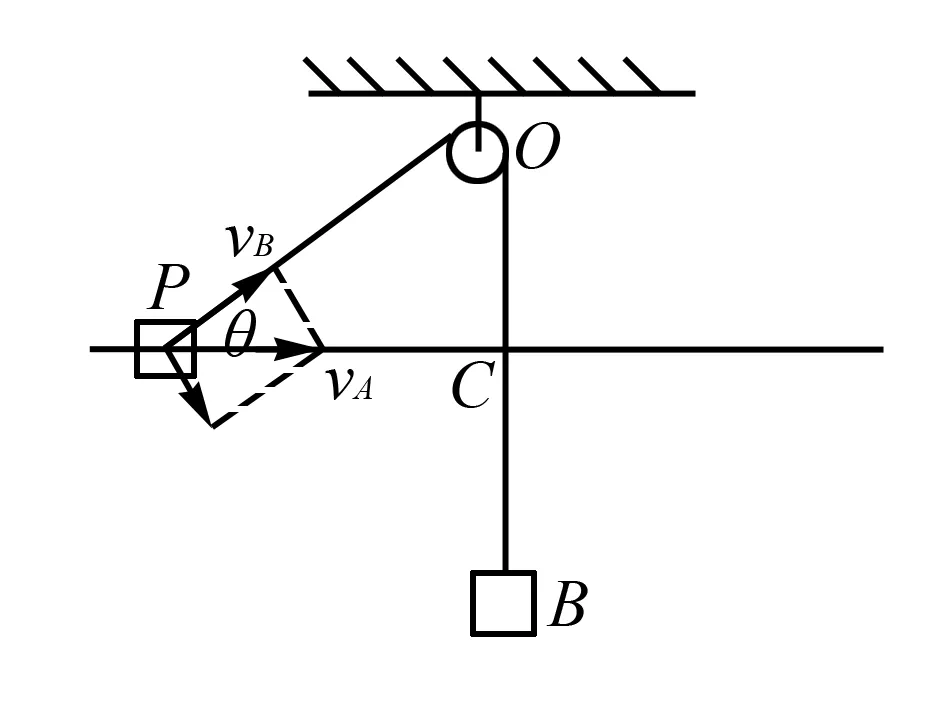
图5
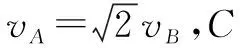
那么B的最大速度到底在什么时候出现呢?根据A、B二者的速度关系和系统机械能守恒可以列式:
vAcosθ=vB
(2.1)
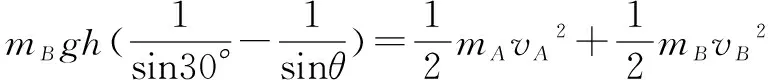
(2.2)
进而可以得到vB的表达式:
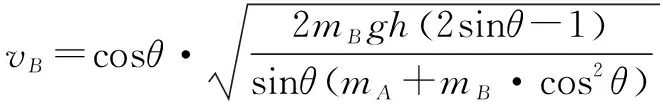
(2.3)
虽然得到了vB表达式,但它形式复杂,仅使用高中数学知识难以求得其最值的解析解.故笔者在此选择借助MATLAB软件求取其最值的数值解.
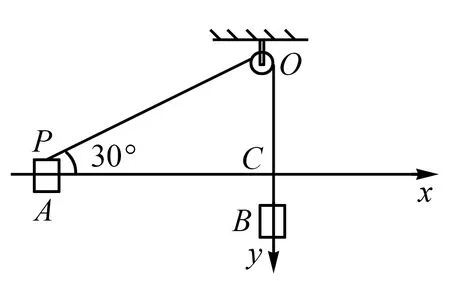
图6
如图6所示,沿水平长杆建立x轴,设物体A在初始位置时,物体B的位移也为0,那么当物体A位于C点时,物体B的位移达到最大值ymax=2h.令绳OP与x轴正方向的夹角为θ,则有:
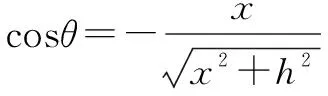
(2.4)
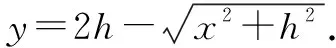
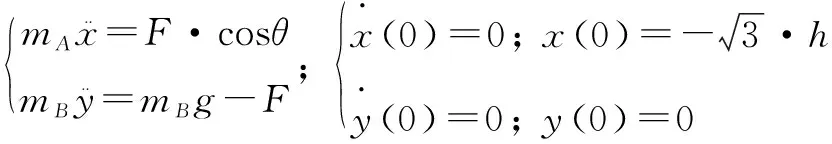
(2.5)
根据y坐标的表达式可以进一步得到:
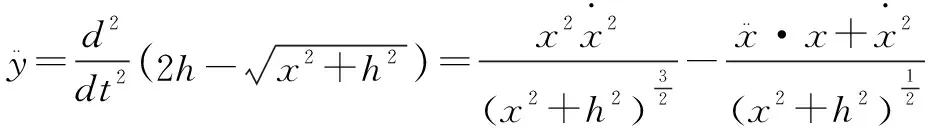
(2.6)
为了方便分析不妨设A和B的质量相等,那么综上所述,式(2.5)可化成:
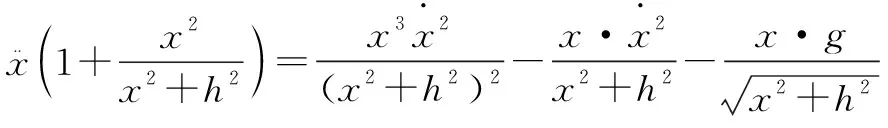
(2.7)
设高度h=10 m,重力加速度g=10 m/s2,物体的质量mA=mB=1 kg,把图6所示位置作为初始位置开始计时,使用MATLAB求解,可以得到A和B的速度分别随角度θ、时间t、A的位移x的变化曲线如图7(a)、(b)和(c)所示.
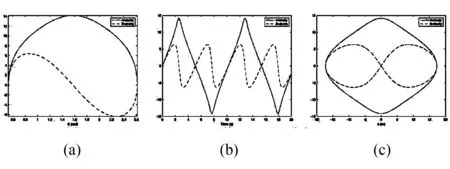
图7
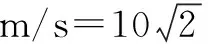
点评绳约束物系问题考查了学生灵活使用合成和分解思想处理动力学问题的能力.如表2所示,本题中的两个物体虽是由一根轻绳相连,但各自速度的大小、变化趋势乃至改变周期都不相同.学生需要把握轻绳约束物系相关速度的本质特点,理智分析才能做出正确判断.
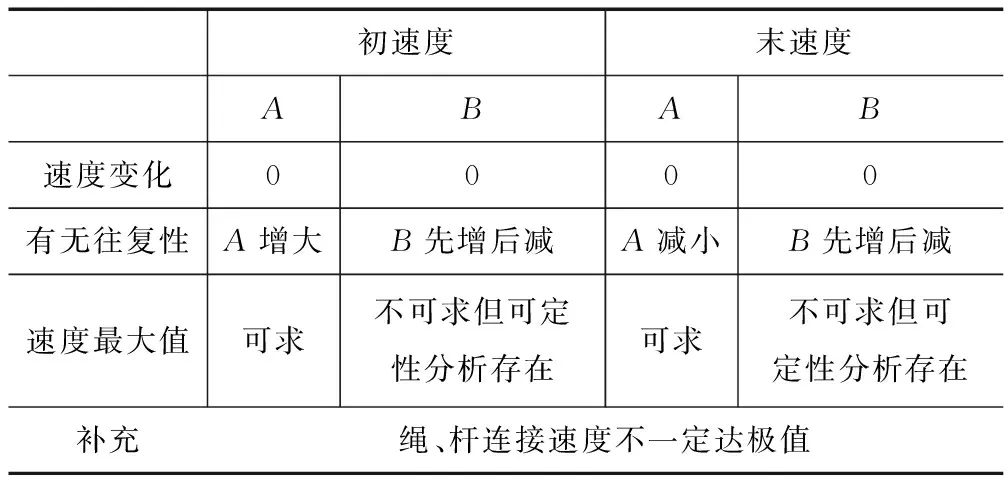
表2 A、B两物体的速度变化趋势对比
例5 (2015·全国卷Ⅱ)如图8所示,滑块a、b的质量均为m,a套在固定竖直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点,重力加速度大小为g,则( ).
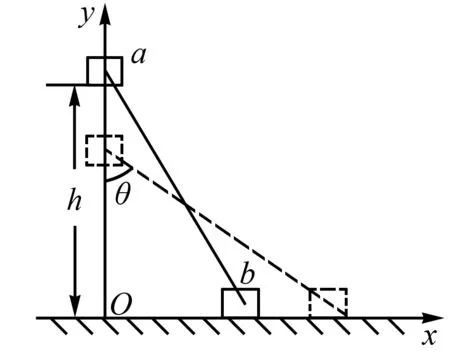
图8
A.a落地前,轻杆对b一直做正功
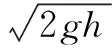
C.a下落过程中,其加速度大小始终不大于g
D.a落地前,当a的机械能最小时,b对地面的压力大小为mg
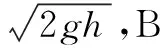
点评b速度最大的位置到底在哪呢?为了便于谈及不妨设b速度最大时,刚性杆与水平方向的夹角为θ,若杆长为L,由a、b二者的速度关系和系统机械能守恒,可以列式:
vacosθ=vbsinθ
(2.8)
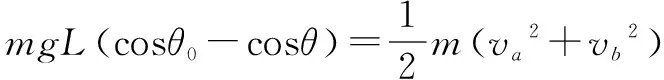
(2.9)
由式(2.8)和 式(2.9)可得a、b二者的速度分别和夹角θ的关系:
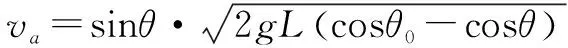
(2.10)
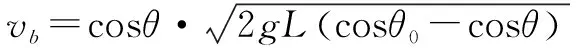
(2.11)
由式(2.10)和式(2.11)可知a块的速度恒增加,b块的速度先增加后减小,其最大极值可由均值不等式或求导法来求得.本文采用求导的方法,对vb表达式(2.11)求导可得:
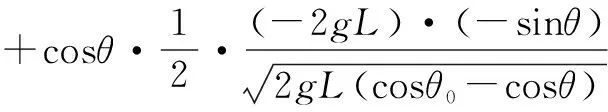
(2.12)
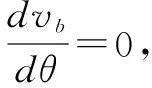

(2.13)
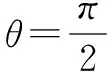
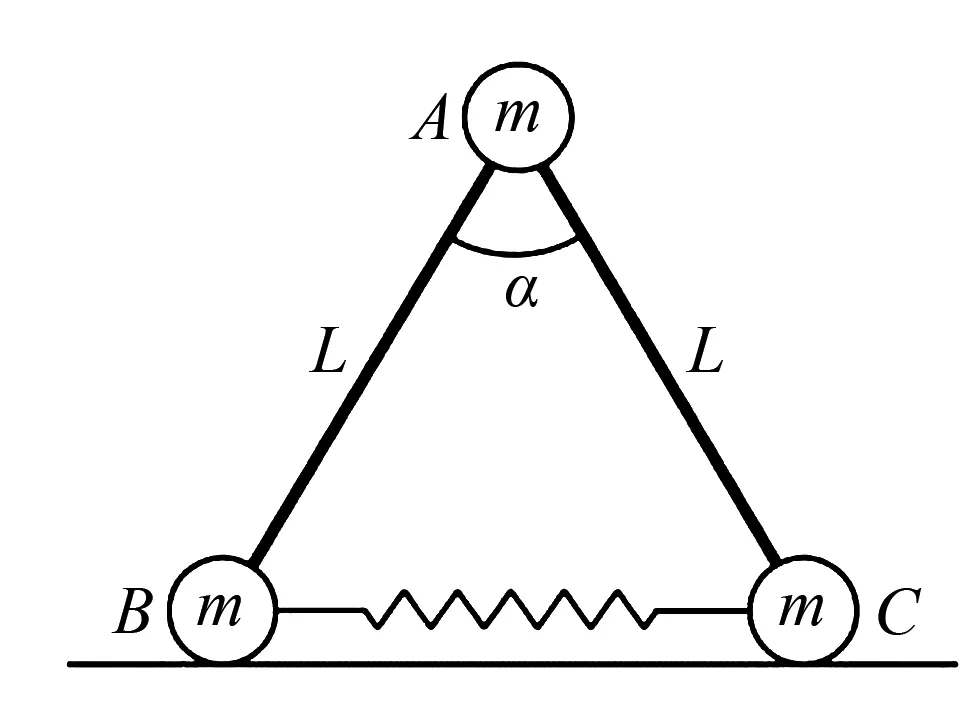
图9
例6 (2017·江苏高考)(多选)如图9所示,三个小球A、B、C的质量均为m,A与B、C间通过铰链用轻杆连接,杆长为L.B、C置于水平地面上,用一轻质弹簧连接,弹簧处于原长.现A由静止释放下降到最低点,两轻杆间夹角α由60°变为120°.A、B、C在同一竖直平面内运动,弹簧在弹性限度内,忽略一切摩擦,重力加速度为g.则此下降过程中( ).
A.A的动能达到最大前,B受到地面的支持力小于3mg/2
B.A的动能最大时,B受到地面的支持力等于3mg/2
C.弹簧的弹性势能最大时,A的加速度方向竖直向下
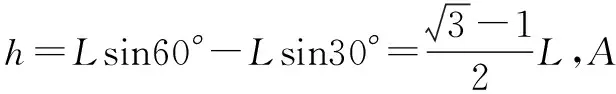
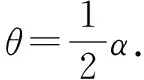
vC·sinθ=-vA·cosθ
(2.14)
(2.15)
其中vB=-vC恒成立.由于α=120°时A到达最低点,即θ=60°时A回归速度为零状态.故根据功能关系有:
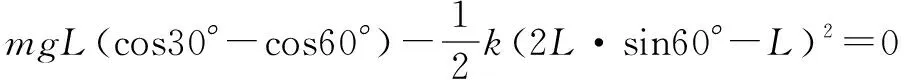
为了进一步研究A、C速度和时间、位置之间的关系,可以建立坐标系如图10所示.设AC间轻杆的作用力大小为F,则有微分方程组:
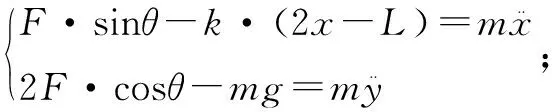
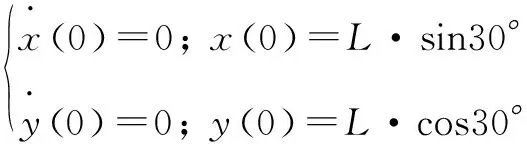
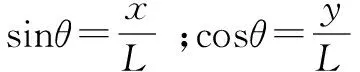
(2.18)
x2+y2=L2
(2.19)
联立上式,最终可以化简得到关于x坐标的微分方程:
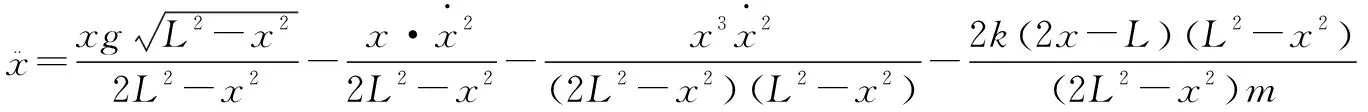
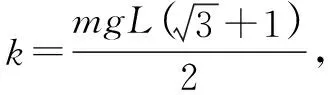
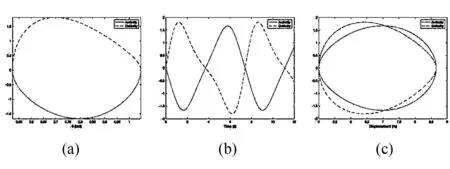
图11
由图11可知,当时间t=1.226 s时,C球第一次达到速度峰值vCmax=1.8097 m/s,此时夹角θ=39.9535°∈[30°, 60°],C球的坐标满足(xC,yC)=(6.44 m, 0 m);随后当时间t=1.604 s时,A球第一次达到速度峰值vAmax=-1.6691 m/s,此时杆AC和y轴的夹角θ=45.6570°∈[30°, 60°],在题设坐标系下A球的坐标(xA,yA)=(0 m, 7.0453 m).A球和C球分别沿y轴和x轴作周期往返运动,与解析中定性分析所得结论一致.
三、“鹿回家”型
例7 在光滑水平面上有一静止的物体,现以水平恒力F1推这一物体,作用一段时间后,换成相反方向的水平恒力F2推这一物体,当恒力F2作用时间与恒力F1作用时间相同时,物体恰好回到原处,求恒力F1和F2的大小之比?
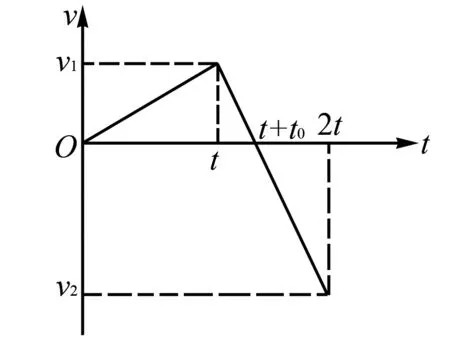
图12
解析设物体的质量为m,在力F1作用下产生的加速度为a1,运动时间t后,发生的位移为x1,获得的速度为v1;在力F2的作用下产生的加速度为a2,经过相同的时间,运动的位移为x2,获得的速度为v2.物体运动过程的v-t图像如图12所示,若作用时间t+t0后速度v=0m/s,则有:
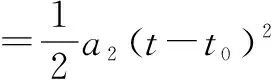
(3.1)
a1t=a2t0
(3.2)
(3.3)
此外,由于整个运动过程中物体质量不变,位移大小相等,时间也相等,故不仅其所受合力之比,其加速度之比、功之比、冲量之比、平均功率之比、动能变化量之比、动量变化量之比均相等且为1∶3.即:
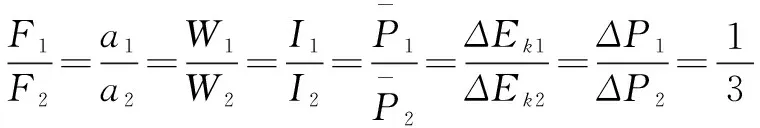
点评值得拓展的是,类似的,若以水平恒力F1推这一物体,作用t时间后换成相反方向的水平恒力F2推同一物体,但却是在经过nt时间之后,物体刚好回到原静止位置,则得到合力之比和速度之比需满足:
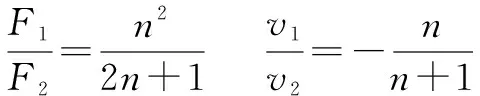
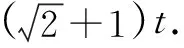
*注:其中“负号”仅表示速度方向和坐标系规定正方向相反,不计入速度大小的比较.

