换元转化 化难为易

叶文明 李 阳

(浙江省松阳二中 323406)

李阳(1991-)，男，中学二级教师，从事高中数学教学研究.

解数学题时，常把某个式子看成一个整体，用一个变量去代替它，从而使问题得到简化的方法叫换元法.换元法的实质是转化，把复杂问题简单化.换元法在研究方程、不等式、函数、数列、解析几何等问题中有广泛的应用，它几乎涵盖高中阶段的所有内容，是一种常用的解题方法.

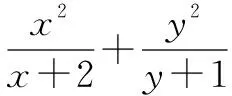
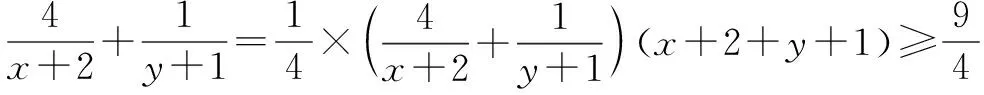
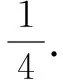
方法二(换元)令x+2=a,y+1=b,则a+b=4.

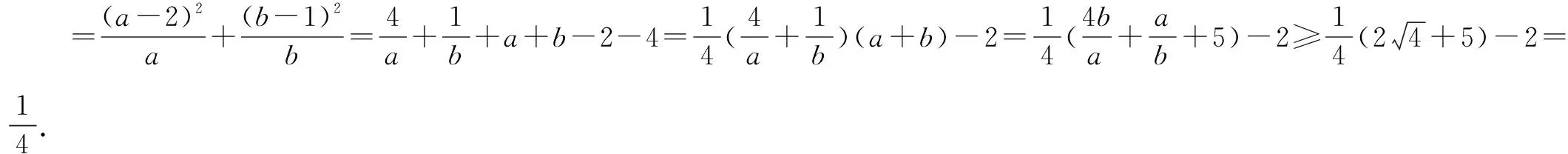
显然换元法容易理解，当分母稍显复杂时，常用换元法化繁为简.

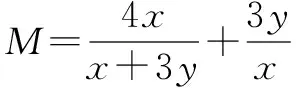
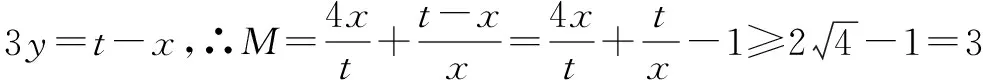
∴M的最小值为3.

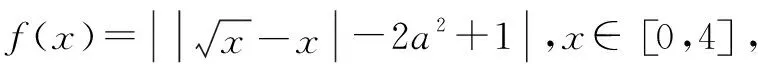
解析绝对值问题通常采用分类讨论去掉绝对值符号的方法解决，但本题直接分类讨论稍显繁琐，采用换元法后再分类讨论则容易得出正确答案.

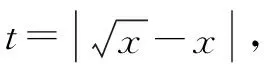
∴当2a2-1≤1，即-1≤a≤1时，如图1所示

g(a)=|2-(2a2-1)|=2-(2a2-1)=-2a2+3，

当2a2-1>1，即a<-1或a>1时，如图2所示.

g(a)=|0-(2a2-1)|=2a2-1

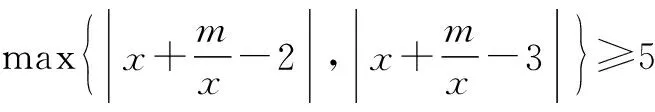
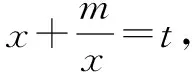
∴m≥(-x2+7x)max，x∈[1,2]，∴m≥10.

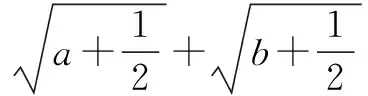
解析求代数式的取值范围，即最值问题时，常用基本不等式解决，当式子较复杂时，可利用换元法化繁为简.

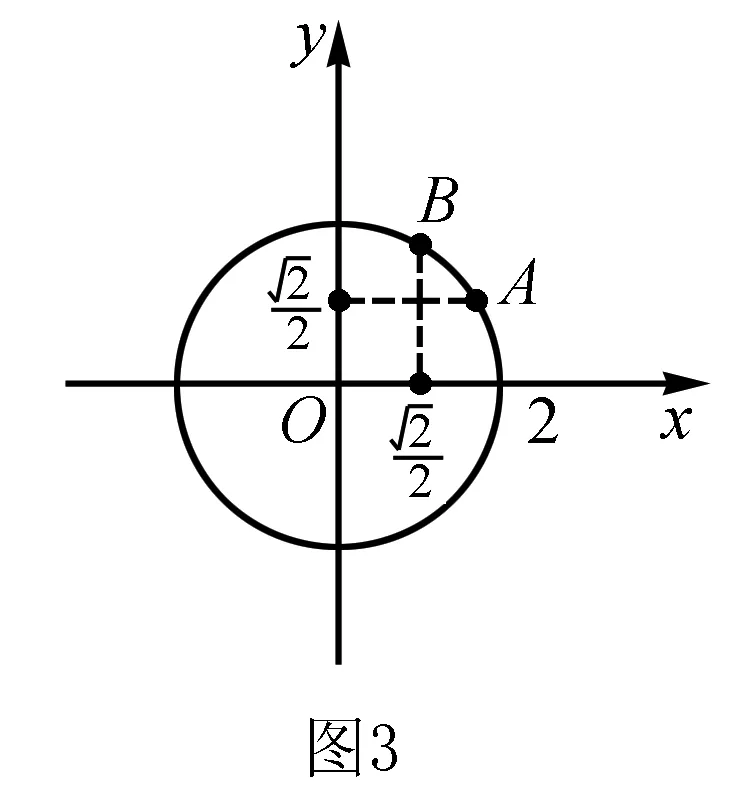
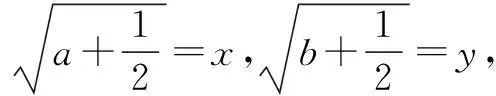
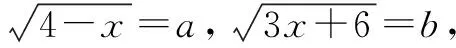
换元法的本质是转化，构造元和设元，通过等价代换，变换对象，将问题转换成新的对象去研究.用换元法解题时要注意以下几点：(1)选择合适的变量换元，遵循让问题简化的原则.(2)换元后要注意新变量的范围，并根据题设加以验证.