剖析向量高考题 抓准复习着力点

宋 磊

(上海南汇中学 201399)

一、高考对向量的考查内容和要求

《普通高中数学课程标准(2017年版2020年修订)》对向量进行了刻画：向量理论具有深刻的数学内涵、丰富的物理背景.向量既是代数研究对象，也是几何研究对象，是沟通几何与代数的桥梁，是描述直线、曲线、平面、曲面以及高维空间数学问题的基本工具，是进一步学习和研究其他数学领域问题的基础，在解决实际问题中发挥重要作用.基于向量的重要性，平面向量是高考的重要考点之一.

高考对平面向量的考查主要有三个层面：知识层面，直接考查向量的线性运算、数量积、垂直或平行关系、基底、模与夹角、向量基本定理等；方法层面，重点考查数形结合、转化与化归、分类讨论、函数与方程等思想方法；素养层面，主要考查数学运算、直观想象、逻辑推理和数学建模等核心素养.2020年全国高考向量试题遵循了“考查基础知识的同时，注重了思想方法和核心素养考查”的原则，很好地考查了知识点、思想方法和数学素养.

二、2020年高考向量试题剖析

平面向量融数、形于一体，具有几何和代数的“双重身份”，由于其知识的特点，在试题的基础性、综合性、灵活性、创新性、难度设计和区分度设计等方面提供了广泛的试题命制空间，因而决定了其必然会成为历年高考试题中的热点内容.笔者以2020年高考数学全国文理和各省市真题卷为例，撷取若干典型问题剖析，以期找寻试题中所含知识要点、思想方法，探求数学本质，感悟核心素养，进而指导和反思向量教学，为2021年高考复习抓准着力点.

1.注重向量基本运算

低中难度的向量问题考查基本上是基于线性运算和数量积运算，以符号形式和坐标形式两种方式，展开平行、垂直、夹角、模等问题的考查.

例1 (2020年新课标Ⅰ文14)设向量a=(1,-1)，b=(m+1,2m-4)，若a⊥b，则m=____.

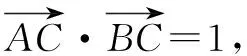
A. 圆B. 椭圆C. 抛物线D. 直线

例3(2020年新课标Ⅱ理13)已知单位向量a,b的夹角为45°，ka-b与a垂直，则k=____.

例4 (2020年新课标Ⅲ理6)已知向量a,b满足|a|=5，|b|=6，a·b=-6，则cos=( ).

例5 (2020年新课标Ⅰ理14)设a,b为单位向量，且|a+b|=1，则|a-b|=____.

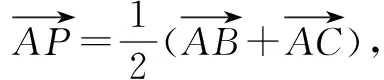
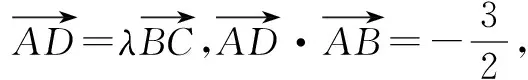
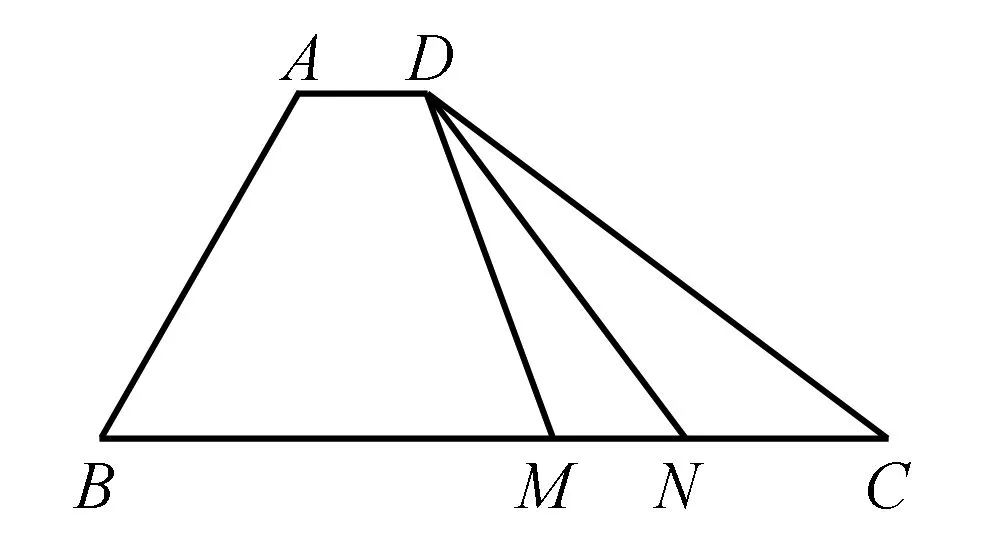
图1

2.注重代数运算与几何推理相结合

由于向量是沟通代数与几何的有力工具，向量问题的解决途径一般有两个：一是代数法，从向量的线性运算、数量积、平面向量基本定理以及坐标表示等方面思考，将问题转化为代数中的有关问题解决；二是几何法，通过向量的几何意义以及向量的基本运算将其转化为平面几何问题.很多向量的综合问题需要代数运算与几何推理相结合.

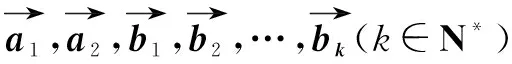
图2

3.突出向量与其它知识的交汇

向量是沟通代数与几何的重要工具，是联系不等式、函数、三角、数列、几何等多项内容的桥梁.因此，向量与其它知识的交汇自然深受高考命题专家的青睐.

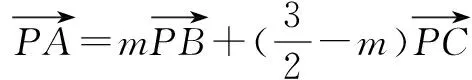
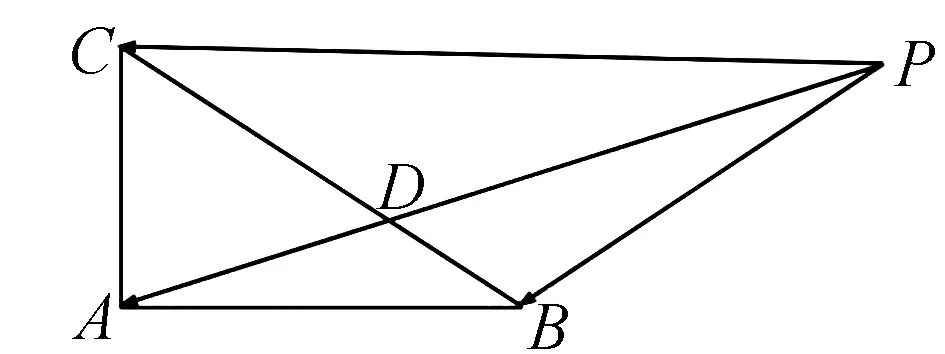
图3

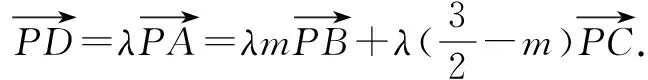
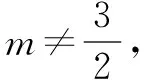
(2)After eliminating the observations affected by multipath by the EM-aided method.Through conversion,the ranging error was reduced to approximately 20%compared with that of dual-frequency ambiguity estimation.

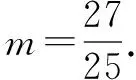
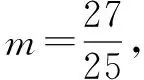
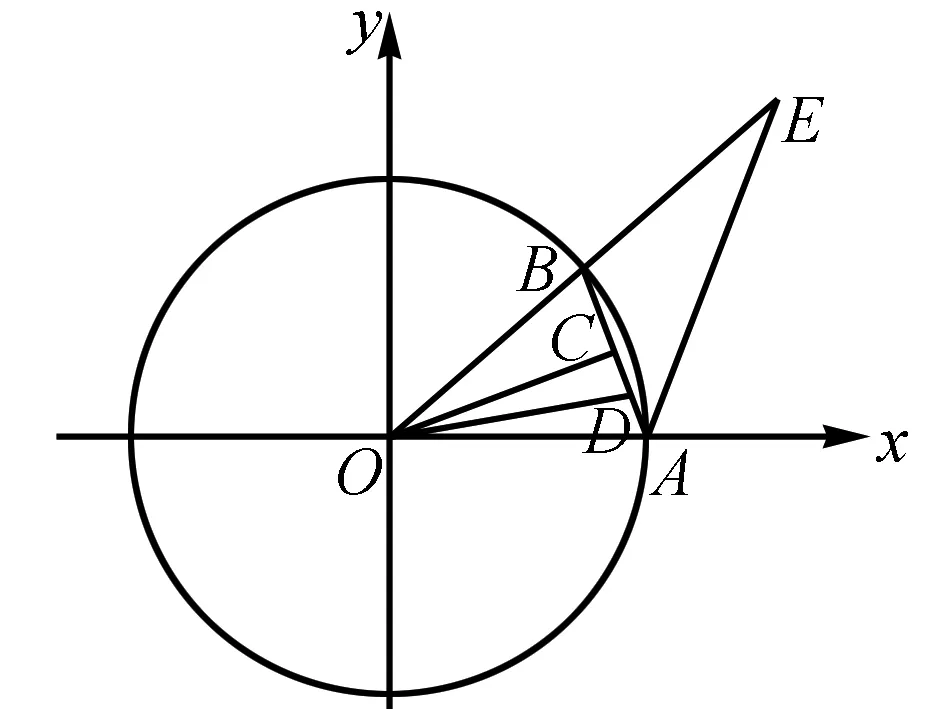
图4

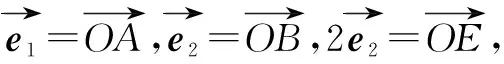
评析方法1、2均采用代数法符号运算，结合不等式、函数相关知识解决；方法3采用坐标法；方法4是转化为几何法解决.

三、抓准向量“三核心”，强化向量“四意识”

通过对2020高考向量试题的剖析，可以帮助我们抓准复习的着力点，建构2021高考复习的框架.笔者认为，应当抓准向量“三核心”，强化向量“四意识”.

1.向量“三核心”

向量复习的第一个核心是加强基本概念与基本运算的复习，主要包括平面向量基本定理、向量的模的运算和几何意义、向量的线性运算、共线向量、向量数量积及相关的向量夹角与向量垂直等内容，基本运算包括符号形式与坐标形式.

向量复习的第二个核心是明确向量代数与几何双角色，凸显双性.在复习过程中，例题的示范要凸显双性，如上文例9、例10一样，让学生感受到手中有两招，可选择可优化，形成代数与几何这两个解题流程.

向量复习的第三个核心是注重平面向量运算工具的灵活使用，纵横交汇.由于平面向量作为沟通代数与几何的桥梁，其研究几何图形性质的工具性的作用非常明显，因此，以平面向量为背景或利用平面向量作为解题工具来命制高考试题，是数学高考试题命制的常见方法.在全面复习的基础上，重视对主干知识和重要思想方法的掌握，掌握向量在知识交汇处的主要考查途径和解决方式，让学生体会关于高考数学命题的新理念.

2.向量“四意识”

第一，向量复习要有“坐标意识”.“坐标法”是解决向量问题的重要途径，其优点是思维方式比较“固定”，学生容易掌握.坐标法的关键是合理建立直角坐标系，准确算出关键点的坐标.如上文例2、例6、例7均可以用坐标法解决.

第二，向量复习要有“几何意识”.我们要引导学生主动挖掘向量问题的几何背景用以解题.很多时候，我们如果能将向量问题置于适当的几何背景之中，就能够使抽象问题直观化，将复杂的代数问题转化为几何问题，从而快速求解.

第三，向量复习要有“投影意识”.向量的数量积是向量非常重要的核心知识，而投影对向量数量积本质的理解和把握，起到了关键作用，在向量复习中要强化向量投影的意义和价值的认识.在解决向量数量积问题时，利用投影可能会事半功倍.

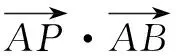
A.(-2,6) B.(-6,2)

C.(-2,4) D.(-4,6)

图5

第四，向量复习要有“基底意识”.平面向量基本定理是向量知识体系中占有核心地位的定理，而“基底意识”的本质就是平面向量基本定理的灵活运用，难点是如何选择“基底”用于简化运算.上文中，例6、例7、例9、例10都可以用“基底思想”来解决.