中职“直线与圆锥曲线”专题解题分析
李士荣
(江苏省吴江中等专业学校 215200)
直线与圆锥曲线类题型,是一种兼具对学生基础考察和能力检测的题型.当此类题型出现在选择、填空及解答题型中时,往往是出于学生对圆锥曲线的定义、标准方程等基础知识点的考察,只要学生们按部就班、仔细研判,通常不难得到正确答案.而当此类题型出现在解答题中,往往会与圆锥曲线的轨迹、位置、弦长、最值等相关联,需要学生能够融合函数、方程、几何等知识点,并对数形结合、空间想象及复杂类计算等能力实施考察.
一、直线与圆锥曲线的基础性质类题型
对于直线与圆锥曲线基础性质类问题,其往往是考察一个圆锥曲线与一条或多条直线之间的组合关系,又或者是与其它平面图形相联系,对学生关于圆锥曲线知识点的掌握进行全面考察.结合长期的教学经验,针对此类基础类题型,可以通过采用待定系数法的方式,从而实现快速求解.

图1
例1 已知双曲线的两个定点分别为A、B,且点M为双曲线上的任意一点,其中点A、B、M组成的△ABM为等腰三角形,其钝角为120°,求双曲线的离心率.
分析结合题中已知条件可知,欲求解本题,等腰三角形是最重要的条件.不妨使用待定系数法,假设双曲线方程,利用等腰性质实现求解.

二、直线与圆锥曲线的位置关系类题型
求解直线与圆锥曲线的位置关系时,待定系数法往往是最直接的方法,通过假设直线方程为Ax+By+C=0(A,B不同时为0),利用待定系数的方法,将其代入圆锥曲线的表达式,此时,利用消元法消去其中一个未知数,得到关于另外一个未知数的方程,再分类讨论a≠0及a=0的情况下,便可实现判断.

分析针对此题,可以利用待定系数法假设直线l的方程,再与抛物线联立方程组消元求解,并结合交点个数,求解直线方程.
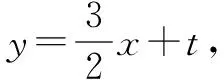
三、直线与圆锥曲线的弦长类问题


分析本题虽说包含直线、双曲线和抛物线,并存在交点、中点等,但若是利用点差法,假设处各个点的坐标,联立方程组,并结合已知条件,便可实现顺利求解.
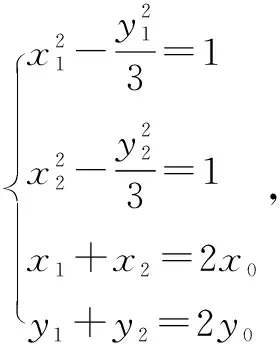
四、直线与圆锥曲线的最值类问题
圆锥曲线最值问题的题型众多,但最终的求解方法无异于两类.一是几何求解方法,即是利用圆锥曲线的定义、性质及定理等实施求解;二是利用代数的方法进行求解,即是将最值求解的几何量或表达式转化成函数或不等式的形式进行求解.

分析针对该四边形面积的最值求解,其最大值较为明显,即是当其中一条直线经过通径时,故本题的难点就在于判断何时四边形面积取得最小值.其核心方法就是建立关于面积变量的目标函数.


总之,对于直线与圆锥曲线的试题类型众多,解题方法也是千变万化.但无论如何,其基本考点无非是对圆锥曲线的概念、性质、交点及轨迹等,有效求解方法无非是待定系数、点差法等.相对重点题型的一对一训练,更重要的还是从题干入手,结合各题的已知条件及类型,找出针对性的求解方法,实现对症下药,从而快捷高效求解.

