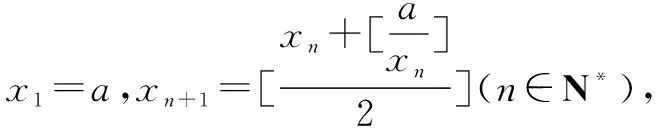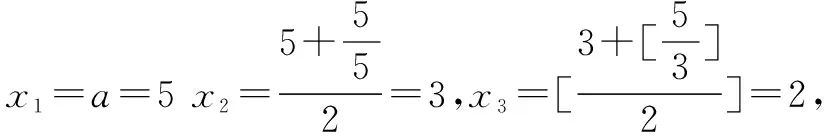高斯函数[x] 性质及其应用
文贵双
(甘肃省天水市一中 741000)
高考试题根植于教材,但又不断创新,将教材内容与高等数学巧妙结合,成为高考、竞赛的热点.高斯函数就是一个好的结合点,高斯函数出现在教材的习题中,各类考试中都有高斯函数的“倩影”,此类问题新颖灵活,能更好考查学生的思维品质和数学素养.
高斯函数也叫取整函数.取整函数[x]表示不大于x的最大整数,且由于对于任意的实数x,对应的函数值[x]都是整数,故称函数y=[x] 为取整函数.
[x]满足下面几条简单性质
(1)[x] 是整数.
(2)[x]≤x<[x]+1.
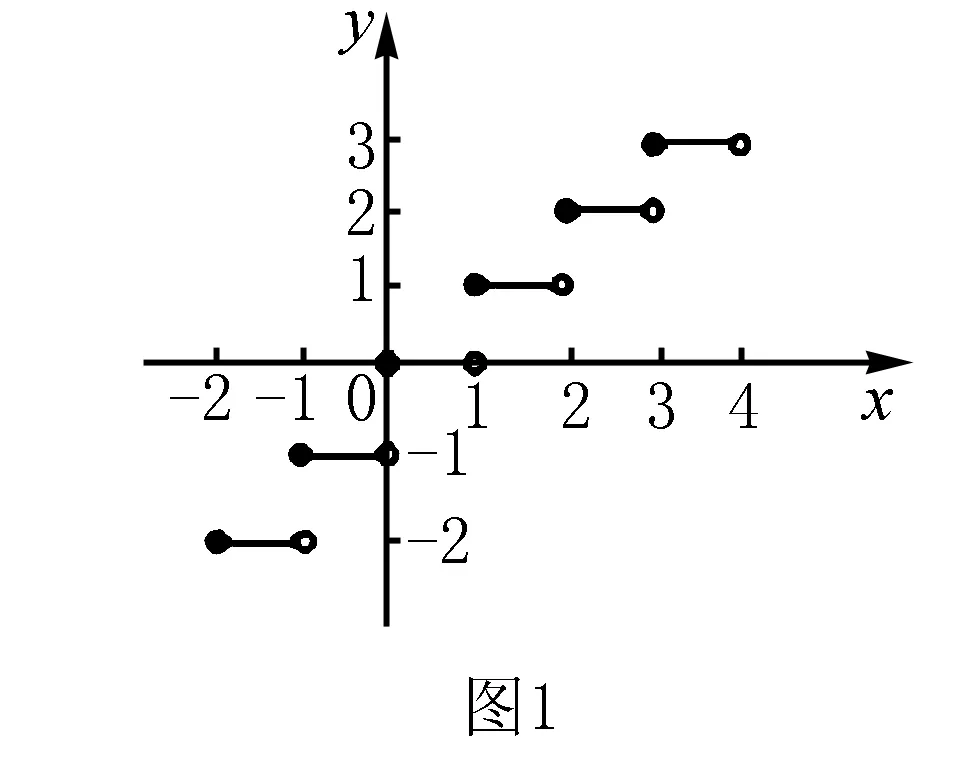
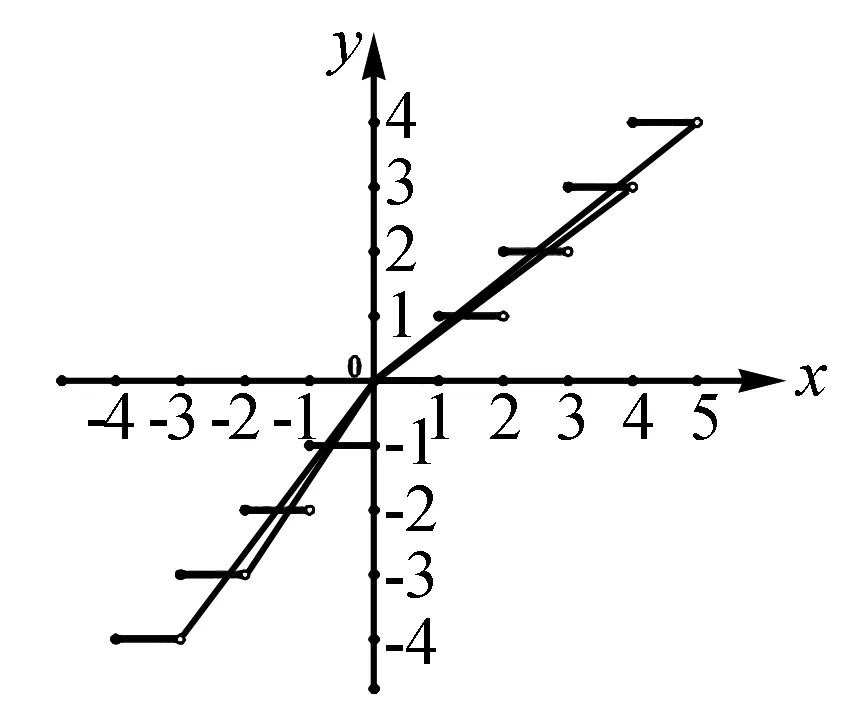
(3)取整函数是一个不减函数,即对任意x1,x2∈R, 若x1 (4) 若x,y∈R,则[x]+[y]≤[x+y]≤[x]+[y]+1 (5) 若n是正整数,x∈R,则[nx]≥n[x] (6) 若m是整数,则[x+m]=[x]+m,y=[x]的图象如图1所示.其图象是一组阶高为1的平行与x轴的线段,不包括右端点,这组平行线段成阶梯状,故取整函数亦称阶梯函数. 而函数f(x)=x-[x]称为x的非负纯小数部分,并用“{x}”表示.任意一个实数都能写成整数与非负纯小数之和,即:x=[x]+{x},其中{x}∈[0,1)称为小数部分函数.f(x)=x-[x]图象如图2所示,是一个周期函数. 高斯函数[x]是一个非常有趣的数论函数,在许多数学分支中都有广泛的应用,在高中数学竞赛和高考试题中也经常出现与高斯函数有关的试题. 由于高斯函数[x]性质不如初等函数(利如二次函数,指数函数、对数函数、三角函数)多,使用起来不方便.所以涉及取整函数[x]的题目,有其特殊的技巧,下面举例说明其解法. 例1Sn为等差数列{an}的前n项和,且a1=1,S7=28.记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1. (1)求b1,b11,b101; (2)求数列{bn}的前1000项和. 故b1=[lga1]=[lg1]=0,b11=[lga11]=[lg11]=1,b101=[lga101]=[lg101]=2. (2)记{bn}的前n项和为Tn,则T1000=b1+b2+…+b1000=[lga1]+[lga2]+…+[lga1000]. 当0≤lgan<1时,n=1,2,…,9; 当1≤lgan<2时,n=10,11,…,99; 当2≤lgan<3时,n=100,101,…,999; 当lgan=3时,n=1000. 故T1000=0×9+1×90+2×900+3×1=1893 例2 求 [log21]+[log22]+[log23]+…+[log22012]的值. 解[log21]=0,[log22]=1,[log23]=1,[log24]=[log25]=[log26]=[log27]=2, 当2k≤n<2k+1时,[log2n]=k,k,n是自然数,故有: 原式=0+1×(22-2)+2×(23-22)+…+9×(210-29)+10×(2012-1023) =1×2+2×22+3×23+…9×29+9890=8194+9890=18084 评注 例1,例2不需要什么技巧,只要理解取整函数的概念即可解决问题. 图3 A.函数f(x)在(m+1,+)上的值域为 B.函数f(x)图象关于直线x=m对称 C.函数f(x)在(m,+)是减函数 D.函数f(x)在(m+1,+)上的最小值为 图4 评注型如[ax+b]=cx+d或[ax+b]+[cx+d]=e的方程通常利用取整函数的定义与性质,结合换元法求解. 当a=1时,x1=1,x2=x3=…=xn=1,但当a=3时,x1=3,x2=2,x3=1,x4=2,x5=1,x6=2,x7=1,…,此时可以看出数列{xn},从第二项起是以2为周期重复出现,不存在正整数k,使得当n≥k时总有xn=xk,故②不正确. 评注本题借用取整函数,构造一个新数列,主要考查数列知识的灵活应用和推理论证能力.本题是取整函数(高斯函数)与数列二者交汇而成,设计新颖,构思精妙,难度较大.解此类题的关键是理解函数[x]的意义.
一、有关高斯函数求值题
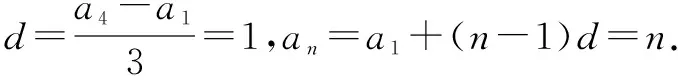
二、有关高斯函数图象题
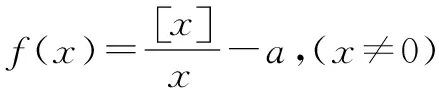


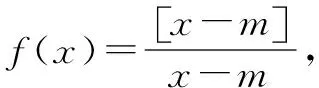

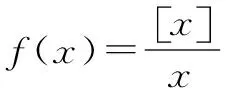
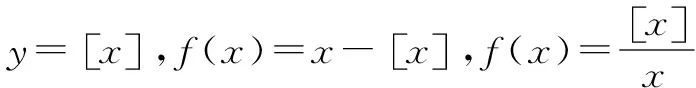
三、有关高斯函数方程题


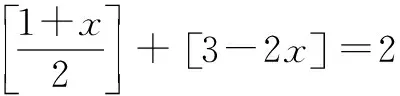
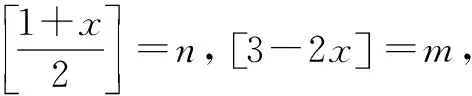
四、有关高斯函数的数列题