2020年清华大学强基计划数学试题及其详解

甘志国

(北京丰台二中 100071)

基金项目：北京市教育学会“十三五”教育科研滚动立项课题“数学文化与高考研究”(课题编号：FT2017GD003)

全卷共20道不定项选择题.以下试题是回忆版，但对准备参加重点大学强基计划考试的读者仍有重要参考作用.

该试题较其他2020年重点大学强基计划的数学试题难度都要大.针对下面的试题题号按难度渐升的顺序叙述如下：第8题是简易逻辑问题；第16题是立体几何中的空间角问题；第1题是求二元函数的最值；第17题考查函数的奇偶性；第5,7题是平面解析几何问题(后者是双曲线与三角函数的综合)；第15题是反三角函数问题；第2题是平面几何问题；第9题是平面向量问题；第13题是空间向量问题；第12题是求期望(但涉及无穷递缩等比数列各项的和)；第18题涉及定积分与导数；第19题是关于数列前n项和的新定义问题；第10题是求极限(涉及反三角函数及不易想到的裂项法求数列前n项和)；第3题是集合与排列组合的综合；第4题是递推数列问题；第6,14题是初等数论中的整数性质问题；第11题是概率与整数性质的综合问题(用枚举法求解时情况较多)；第20题是定积分.

一、试题呈现

1.若x2+y2≤1(x,y∈R)，则x2+xy-y2的取值范围是( ).

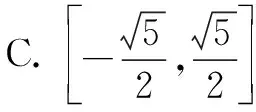
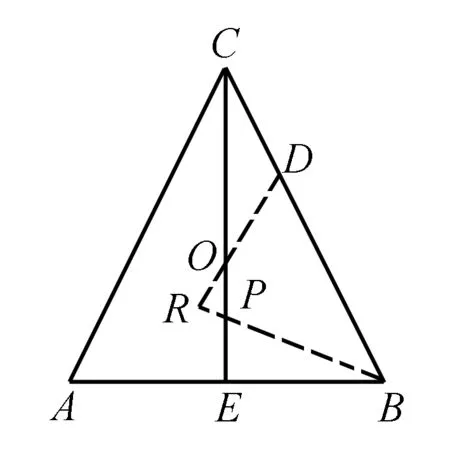
2.在非等边ΔABC中，BC=AC，点O,P分别是ΔABC的外心与内心.若点D在边BC上且OD⊥BP，则下列选项正确的是( ).

A.B,D,O,P四点共圆 B.OD∥AC

C.OD∥ABD.DP∥AC

3.若A,B,C⊆{1,2,3,…,2020},A⊆C,B⊆C，则有序集合组(A,B,C)的组数是( ).

A.22020B.32020C.42020D.52020

A.0 B.2 C.10 D.12

6.若一个三角形的各边长均为整数且其面积为有理数，则该三角形某一边的长可以是( ).

A.1 B.2 C.3 D.4

C.S△PABtan(α+β) D.S△PABcot(α+β)

8.甲、乙、丙三人做同一道题.甲说“我做错了”，乙说“甲做对了”，丙说“我做错了”，老师说“有且仅有一人做对，有且仅有一人说错了”.若老师说的话一定正确，则( ).

A.甲说的对 B.乙说的对

C.丙说的对 D.甲、乙、丙说的均不对

A.∠APB=120°B.∠BPC=120°

C.2BP=PCD.AP=2PC

11.若从0,1,2,…,9中选取5个两两互异的数字依次排成一个五位数(包括0在首位的五位数，其大小就是把0去掉后的四位数)，则它能被396整除的概率是( ).

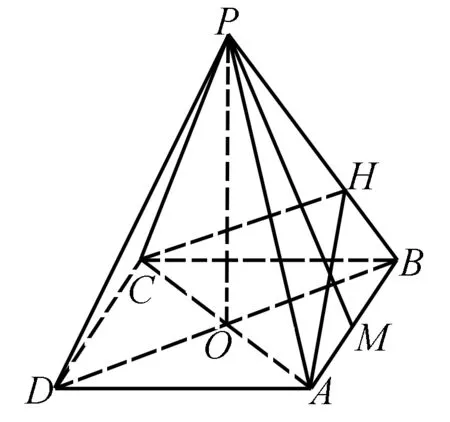
13.若空间向量a,b,c满足|a|≤1,|b|≤1,|a+2b+c|=|a-2b|，则|c|的最值为( ).

C.最小值为0 D.最小值为2

14.若x,y∈N*，则下列说法正确的是( ).

A.x2+2y与y2+2x可以均为完全平方数

B.x2+4y与y2+4x可以均为完全平方数

C.x2+5y与y2+5x可以均为完全平方数

D.x2+6y与y2+6x可以均为完全平方数

16.若某个正四棱锥的相邻两个侧面所成二面角的大小为α，侧棱与底面所成线面角的大小为β，则( ).

A.cosα+tan2β=1 B.secα+tan2β=-1

C.cosα+2tan2β=1 D.secα+2tan2β=-1

A.2 B.e C.3 D.4

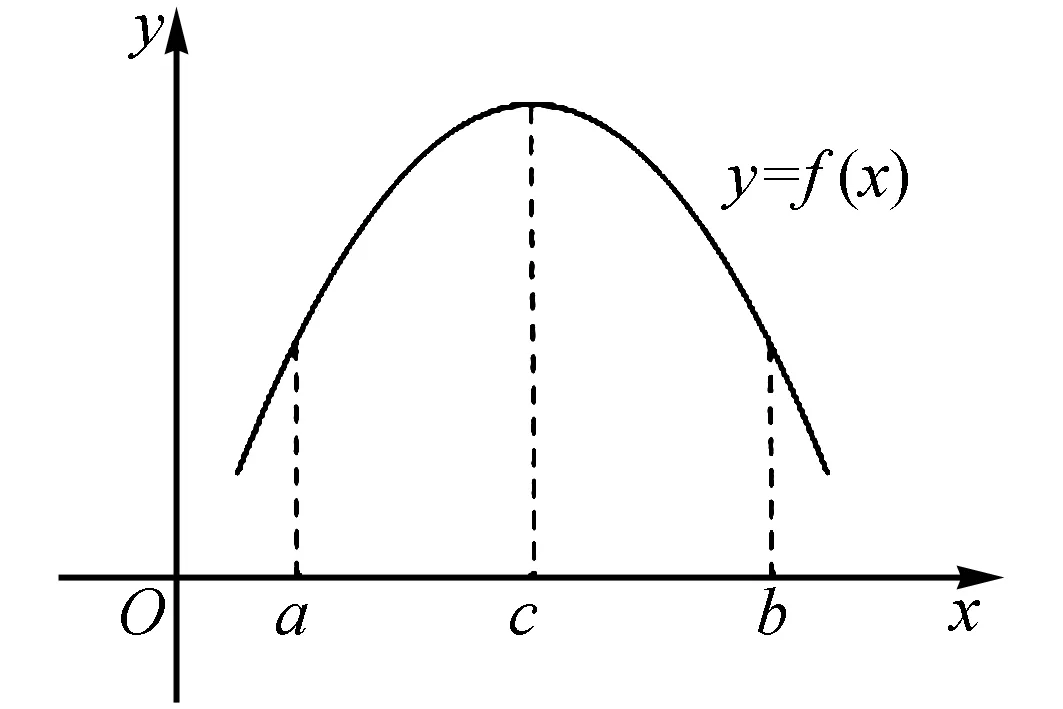
图1

18.已知y=f(x)是上凸函数，x=c是其极大值点，函数y=f(x)的部分图象如图1所示.若函数y=f(x)的图象与直线x=a,x=t(a

A.f(b),f′(a) B.f′(a),f(b)

C.f(c),f′(a) D.f′(a),f(c)

19.把数列{an}的前n项和记作Sn.若∀n∈N*,∃m∈N*,Sn=am，则称数列{an}为“某数列”.以下选项中正确的是( ).

B.若an=k(k为常数)，则{an}为“某数列”

C.若an=kn(k为常数)，则{an}为“某数列”

D.对于任意的等差数列{an}，均存在两个“某数列”{bn},{cn}，使得an=bn+cn

二、试题解析

图2

2.AD.由题设，可得点O,P不重合.

如图2所示，可得点O,P在等腰△ABC底边上的高CE上(点E是边AB的中点).

可设直线OD,BP交于点R，可得∠R=∠CEB=90°，所以O,R,E,B四点共圆.

再由题设“点P是△ABC的内心”，可得∠CBP=∠RBE=∠ROP，所以B,D,O,P四点共圆，得选项A正确.

由B,D,O,P四点共圆，可得∠BDP=∠BOP.

由题设“点O是△ABC的外心”，可得∠BOP=2∠BCO=∠BCA，所以∠BDP=∠BCA.所以DP∥AC，得选项D正确，选项B错误.

若OD∥AB，由CE⊥AB，可得CE⊥OD.又由PB⊥OD，可得PB∥CE.而直线PB,CE交于点P，所以选项C错误.

3.解法1 D.若集合C已确定，由A⊆C可得集合A有2|C|种可能(其中|C|表示集合C的元素个数)；同理，由B⊆C可得集合B有2|C|种可能.所以有序集合组(A,B)的组数是2|C|·2|C|=4|C|.

图3

解法2 D.如图3所示，其中U={1,2,3,…,2020}，可得元素1,2,3,…,2020均有5种填法：UC,U(A∪B),A(A∩B),A∩B,B(A∩B).由分步乘法计数原理，可得所求答案是52020.

4.BC.先用数学归纳法证明a2k,a2k+1(k∈N)分别是偶数、奇数.

当k=0时成立,a0=0,a1=±1.

假设k=n时成立,即a2n,a2n+1分别是偶数、奇数.

可得|a2n+2|=|a2n+1+1|，所以a2n+2是偶数；再由|a2n+3|=|a2n+2+1|，可得a2n+3是奇数.所以k=n+1时也成立.所以欲证结论成立.

由题设，得a2k=a2k-1+1或a2k=-a2k-1-1(k∈N*)，所以a2k-1+a2k=2a2k-1+1或a2k-1+a2k=-1(k∈N*).

可设a2k-1=2m-1(m∈Z)，当a2k-1+a2k=2a2k-1+1时，可得a2k-1+a2k=4m-1.

所以总有a2k-1+a2k≡-1(mod 4).

6.CD.因为三边长分别是3,4,5的三角形的面积6是有理数，所以选项D正确.

若满足题设的三角形的某一边长可以是1，则可设其另外边长分别是b,c(1≤b≤c;b,c∈N*).

由“三角形两边之和大于第三边”，可得1+b>c，即1+b≥c+1,所以b≥c，所以b=c.

若满足题设的三角形的某一边长可以是2，则可设其另外边长分别是b,c(2≤b≤c;b,c∈N*).

由“三角形两边之和大于第三边”，可得2+b>c，即2+b≥c+1,所以b≥c-1.所以b=c-1或c.

所以选项B错误.

故选项A正确.

故选项C正确、D错误.

8.A.若仅甲说的对，则甲做错了；可得乙、丙均说错了，得丙做对了.满足题设“有且仅有一人做对，有且仅有一人说错了”.

若仅乙说的对，则甲做对了；可得甲、丙均说错了，得丙也做对了.不满足题设“有且仅有一人做对”.

若仅丙说的对，则丙做错了；可得甲说错了，得甲做对了；还可得乙说错了，得甲也做错了.前后矛盾！

综上所述，可得仅甲说的对.

图4

同理，可得∠BPC=∠BPA.

再由∠APC+∠BPC+∠BPA=360°，可得∠APC=∠BPC=∠BPA=120°，因而选项A,B均正确.

在Rt△ABC中，可得∠BAC=30°,∠ACB=60°.

11.C.可得396=4×9×11.

若排成的五位数是9的倍数，则这5个数字之和是9的倍数，进而可得所选取的5个数字只可能是0,1,2,6,9；0,1,2,7,8；0,1,3,5,9；0,1,3,6,8；0,1,4,5,8；0,1,4,6,7；0,2,3,4,9；0,2,3,5,8；0,2,3,6,7；0,2,4,5,7；0,3,4,5,6；0,3,7,8,9；0,4,6,8,9；0,5,6,7,9；1,2,3,4,8；1，2,3,5,7；1,2,4,5,6；1,2,7,8,9；1,3,6,8,9；1,4,5,8,9；1,4,6,7,9；1,5,6,7,8；2,3,5,8,9；2,3,6,7,9；2,4,5,7,9；2,4,6,7,8；3,4,5,6,9；3,4,5,7,8之一.

若所选取的5个数字是0,1,2,6,9，由排成的五位数是4的倍数，可得末两位数只可能是20,60,12,92,16,96之一.

再由排成的五位数是11的倍数，可得排成的五位数只可能是10692,60192,10296,20196之一.

又由4,9,11两两互质，所以得到的4个五位数均满足题设.

进而可得满足题设的五位数共96个：10692,60192,10296,20196,17820,87120,21780,71280,08712,78012,07128,17028,13860,83160,31680,61380,08316,38016,03168,13068,15840,85140,41580,51480,01584,51084,05148,15048,30492,40392,29304,39204,37620,67320,23760,73260,06732,76032,02376,32076,47520,57420,25740,75240,04752,74052,07524,57024,35640,65340,43560,53460,03564,53064,04356,34056,68904,98604,60984,90684,38412,48312,21384,31284,14652,64152,14256,24156,87912,97812,81972,91872,47916,97416,41976,91476,57816,87516,51876,81576,85932,95832,83952,93852,76824,86724,72864,82764,46728,76428,42768,72468,45936,95436,43956,93456.

注用电脑编程可以验证上述答案是正确的.

所以随机变量Y的期望是

13.BC.由题设，可得

|a-2b|=|a+2b+c|≥|c|-|a+2b|,

|c|≤1·|a+2b|+1·|a-2b|.

由柯西不等式，可得

(1·|a+2b|+1·|a-2b|)2≤(12+12)(|a+2b|2+|a-2b|2)=4(|a|2+4|b|2)≤20.

还可得a=(0,1),b=(1,0),c=(0,0)满足题设，进而可得|c|的最小值为0，故选项C正确，D错误.

14.CD.由对称性知，可不妨设x≤y.

对于选项A，由y2

对于选项B，由y2

选x=y=4，得x2+5y=y2+5x=62，故选项C正确.

选x=y=2，得x2+6y=y2+6x=42，故选项D正确.

图5

作AH⊥PB于点H，连接CH，可得α=∠AHC,CH=AH.

还可得2S△PAB=AB·PM=AH·PB.

在△ACH中，由余弦定理，可求得

进而可得secα+2tan2β=-1.

17.A.由“闭区间上的连续函数存在最大值与最小值”，可得函数f(x)的最大值与最小值均存在.

当x∈[0,1]时，g(x)<2，所以函数g(x)的最大值与最小值均存在且互为相反数，可分别设为M,-M.

所以函数f(x)的最大值与最小值分别是1+M,1-M.所以所求答案是(1+M)+(1-M)=2.

18.D.由f(x)是上凸函数，可得f′(x)是减函数，所以当x∈[a,b]时，函数f′(x)的最大值是f′(a).

19.ABD.对于选项A，可求得Sn=2n-1(n∈N*)，所以Sn=an+1(n∈N*)，故选项A正确.

选项C正确.∀n∈N*,Sn=k(1+2+…+n)=a1+2+…+n.

解法2 B.在解法1中，已得

所以

解法3 B.由降幂公式，可得

所以

再由排除法，可知答案是B.