点差法的基本原理及其在高考数学中的简单应用

武增明

(云南省玉溪第一中学 653100)

一、点差法的基本原理

在研究直线被圆锥曲线截得中点弦问题时，设出弦端点坐标，并分别代入圆锥曲线方程得两式，将其两式相减，可得弦的斜率与弦的中点坐标之间的关系式，这种解题方法叫做点差法.

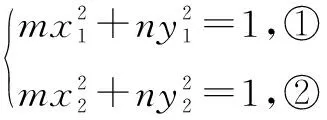
二、点差法的简单应用

与弦中点相关的问题有三种，一是平行弦的中点轨迹；二是过定点的弦的中点轨迹；三是过定点且被定点平分的弦所在直线方程.其他问题都是由这三类问题衍生出来的.

1.已知弦中点坐标简求弦所在直线方程

此类问题是点差法的最基本的简单应用.

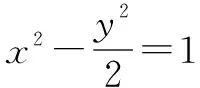
(1)求直线AB的方程；

(2)如果线段AB的垂直平分线与双曲线相交于C，D两点，那么A，B，C，D四点是否共圆，为什么？

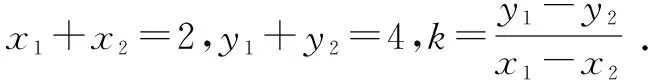
故直线AB的方程为y-2=1·(x-1)，即x-y+1=0.

(2)解略.

评注此问题用常规方法也易求解，但没有用点差法来得快.

2.用点差法简求轨迹方程

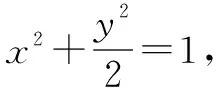
(1)点Q的轨迹方程；

(2)点Q的轨迹与坐标轴的交点的个数.

解(1)设A(x1，y1)，B(x2，y2)，Q(x，y)，则有x1+x2=2x，y1+y2=2y.

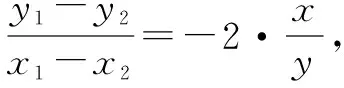
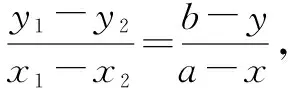
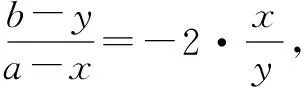
故点Q的方程为2x2+y2-2ax-by=0.

(2)解略.

3.用点差法简求圆锥曲线的方程

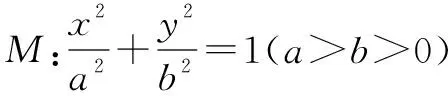
(1)求M的方程；

(2)C，D为M上两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值.

解(1)设A(x1，y1)，B(x2，y2)，P(x0，y0)，则

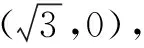
因此，a2=6，b2=3.

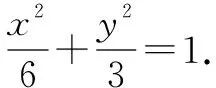
(2)解略.

评注此问题若没有想到点差法，就不易求解了，甚至解不出来.

4.巧用点差法简解对称题型

一般地，对称直线、对称点的题目，用点差法求解较为简便.

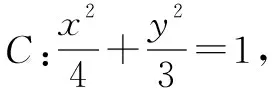
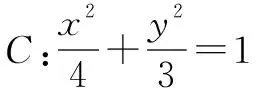
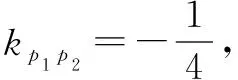
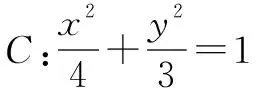
评注解此类题关键是用了点在圆锥曲线内部的充要条件，应认真领会.

5.注意中点的构造，创造点差法的条件简解题

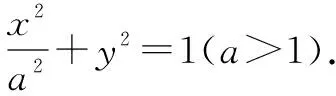
(1)求直线y=kx+1被椭圆截得的线段长(用a，k表示)；

(2)若任意以点A(0，1)为圆心的圆与椭圆至多有3个公共点，求椭圆离心率的取值范围.

分析(1)略.

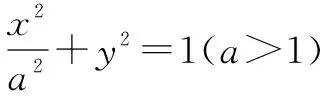
解(1)略.

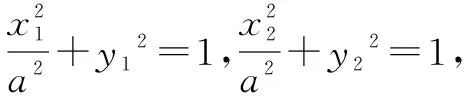
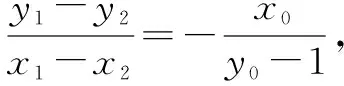
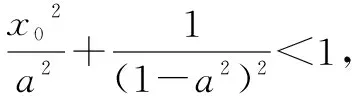
又存在x02∈(0，a2)使上式成立，

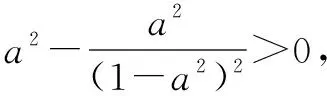
评注(1)命题者(官方)给出的解答计算量较大，详见文[4].(2)此问题，解法较多(详见文[1])，上述解法最简捷.

点差法在高考中有着广泛的运用，如：2010年高考，山东卷·文9，新课标全国卷Ⅰ·理12，安徽卷·理19；2012年高考，湖北卷·理21；2013年高考，新课标全国卷Ⅰ·理10；2015年高考，全国卷Ⅱ·理20，浙江卷·理19；2018年高考，全国卷Ⅲ·理20.

综上所述，点差法在各式各样的题目中均有广泛的应用，同时作为一种基础数学方法，它与其它数学方法之间有着极大的相关性，这是我们在解题过程中所不能忽视的，在学习点差法的解题过程中要熟练掌握运用其它方法，才能够把数学解题思想方法运用到解题过程中，来提高解题效率与质量.