例谈一类含双变量x1、x2的不等式求解问题

张 刚

(安徽省宿州应用技术学校 234000)

含双变量x1，x2的不等式求解问题一直是高考数学的重要考点之一，并且经常以压轴题的形式出现.试题设计经常与函数、不等式结合起来进行考查，同时注重对转化与构造、函数与方程、数形结合等重要的数学思想与方法考查，试题整体难度较大，从而造成学生思维混乱，难以进行深入推理与计算.因此，本文针对这类含双变量x1，x2的不等式求解问题，将结合实例进行分析，寻求此类问题的解题策略，以便于同行交流与探讨.

一、对称转化，借助单调

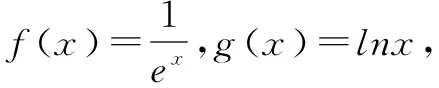
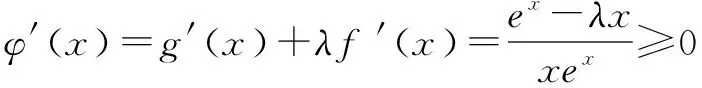
评注由g(x1)-g(x2)>λ[f(x2)-f(x1)]化为g(x1)+λf(x1)>g(x2)+λf(x2)是一种数学对称美的体现，遇到类似的条件句朝着对称的方向转化.这样一来，对于任意的x1>x2>0，总有g(x1)+λf(x1)>g(x2)+λf(x2)成立，就变成了φ(x1)>φ(x2)，这就转化成为函数φ(x)=g(x)+λf(x)在(0,+)上单调递增，最终转化为导数问题.

例2 已知函数f(x)=-lnx-2x2+1，证明对于任意x1，x2∈(0,+)，不等式|f(x1)-f(x2)|≥4|x1-x2|恒成立.

证明f(x)的定义域为(0,+).因为所以f(x)在(0,+)上单调递减.假设x1≥x2，|f(x1)-f(x2)|=f(x2)-f(x1)，则|f(x1)-f(x2)|≥4|x1-x2|⟺f(x2)+4x2≥f(x1)+4x1，令g(x)=f(x)+4x=-lnx-2x2+1+4x，因为所以g(x)在(0,+)上单调递减，故g(x1)≤g(x2).即不等式|f(x1)-f(x2)|≥4|x1-x2|恒成立.

评注含有|f(x1)-f(x2)|的式子关键是去绝对值符号，可以利用单调性去绝对值符号.即对于单调函数f(x)，若x1g(x1)在[a,b]上恒成立⟺g(x)在[a,b]上单调递增，所以g′(x)≥0在[a,b]恒成立.对于含有二元变量x1，x2的函数，可以使变量x1，x2分别位于不等号两边，呈现出不等式左右两边结构一样的对称关系式，便于构造函数模型取解决问题.

二、整体换元，构造函数

例3对任意不相等的正实数x1，x2，试证：

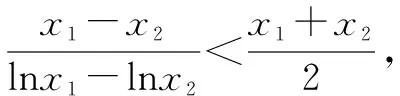
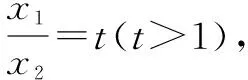
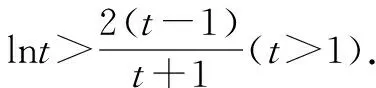
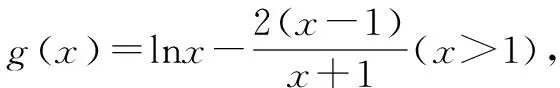
(2)证明：x1x2>e2.

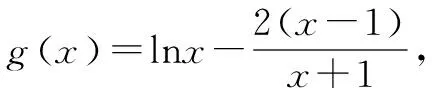
(2)f′(x)=lnx-ax，x1，x2是f(x)的两个极值点，可知x1，x2分别是方程lnx-ax=0的两个根，即lnx1=ax1，lnx2=ax2，设x1>x2，相加得lnx1+lnx2=a(x1+x2)

①

相减得lnx1-lnx2=a(x1-x2)

②

③

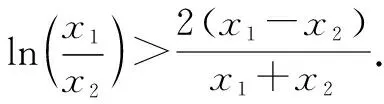
三、关注极值，借助偏移

例5已知函数f(x)=(x-2)ex+3(x-1)2有两个零点，设x1，x2是f(x)的两个零点，证明：x1+x2<2.

解析由题意知f′(x)=(x-1)ex+6(x-1)=(x-1)(ex+6).因为f(x)在(-,1)上单调递减，在(1,+)上单调递增，因此函数的唯一的极值点是x=1.构造函数F(x)=f(x)-f(2-x)=(x-2)ex+3(x-1)2-(-x)e2-x+3(1-x)2=(x-2)ex+xe2-x.

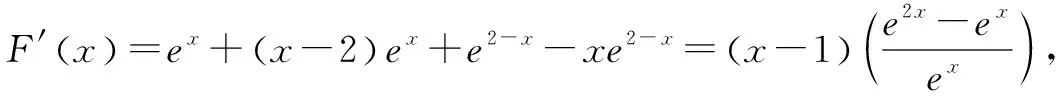
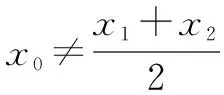
四、等价转化，构造模型

例6函数f(x)=(x-3)ex，对于任意x1，x2∈[1,3]有f(x1)-f(x2)≤a，则实数a的最小值为____.

解析令f′(x)=0，解得x=2，因为f(1)=-2e，f(2)=-e2，f(3)=0，所以f(x)min=-e2，f(x)max=0.又因为对于任意x1，x2∈[1,3]，有f(x1)-f(x2)≤a，所以f(x)max-f(x)min≤a.因为f(x)max-f(x)min=e2，所以a≥e2，故实数a的最小值为e2.

评注|f(x1)-f(x2)|≤f(x)max-f(x)min⟺f(x)min-f(x)max≤f(x1)-f(x2)≤f(x)max-f(x)min.对于任意x1，x2∈D,f(x1)-f(x2)≤a⟺f(x)max-f(x)min≤a;f(x1)-f(x2)≥a⟺f(x)min-f(x)max≥a.

五、依据结构，等价转化

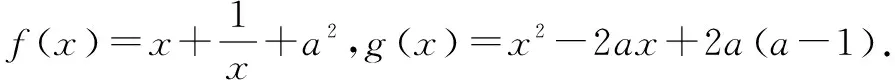
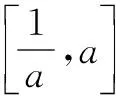
评注对于任意的x1，x2，不等式|f(x2)-f(x1)|≤m恒成立的意义就是函数f(x)在区间内任意两个函数值相差都不超过m，即f(x)max-f(x)min≤m；而存在x1，x2，能满足不等式|f(x2)-f(x1)|≥m的意义是函数f(x)在区间内，至少存在两个函数值相差超过m，即f(x)max-f(x)min≥m,若存在x1∈A，x2∈B，使得|f(x1)-g(x2)|≤m等价于g(x)min-f(x)max≤m，且f(x)min-g(x)max≤m.

六、任意存在，注意区别

例8已知e为自然对数的底数，f(x)=xlnx+a，g(x)=x2ex.

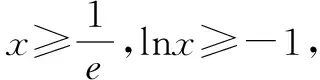
评注若任意x1∈D1总存在x2∈D2使得f(x1)=g(x2)，实质上就是两个函数值域的包含关系，故此类问题利用值域可解;当涉及x2的具体个数时，就不是单纯依靠函数值域就能解决的.如若任意x1∈D1总存在唯一的x2∈D2使得f(x1)=g(x2)，函数g(x)在区间[-1,1]内取一个与f(x1)相等的函数值，对应的自变量的值x2是唯一的.从图形上看，函数g(x)在区间[-1,1]上必须是单调的，且y=f(x1)与函数g(x)图象有且仅有一个交点.