一类恒成立问题处理策略的再延伸
徐加华
(山东省新泰市第一中学 271200)
文[1]利用一个定理解决了一类恒成立问题,本人读后受益匪浅.本文再将该定理推广延伸如下.
定理:(1)已知函数y=f(x)在x=a处可导,且x∈[a,b)时f(x)≤(≥)f(a)恒成立,若函数y=f′(x)在x=a处可导,且f′(a)=0,则f″(a)≤(≥)0.
(2)已知函数y=f(x)在x=b处可导,且x∈(a,b]时f(x)≤(≥)f(b)恒成立,若函数y=f′(x)在x=b处可导,且f′(b)=0,则f″(b)≥(≤)0.
(注:y=f″(x)是函数y=f′(x)的导数.)
对于定理:已知函数y=f(x)在x=a处可导,且x∈[a,b)时有f(x)≤f(a)恒成立,若f′(a)=0.则f″(a)≤0. 我们试着从反面入手说明其正确性.
如果f″(a)>0,则y=f′(x)在x=a处右侧附近的图像单调递增,又f′(a)=0.所以y=f(x)在x=a处右侧附近满足f′(x)≥0.于是y=f(x)在x=a处右侧附近的图像单调递增,从而说明y=f(x)在x=a处右侧附近满足f(x)>f(a),这与条件x∈[a,b)时f(x)≤f(a)恒成立是矛盾的,该定理正确!其他的结论类似说明其正确性.
下面举例说明其应用.
例1已知f(x)=ex-1-x-ax2,当x≥0时,f(x)≥0恒成立,求a的取值范围.
解∵f(x)=ex-1-x-ax2,
∴f(0)=0,f′(x)=ex-1-2ax,f′(0)=0.
f″(x)=ex-2a.
令f″(0)=e0-2a≥0,
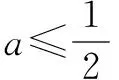
又f′(0)=0,则y=f′(x)在x≥0时有f′(x)≥0,则y=f(x)在x≥0时单调递增,又f(0)=0,从而说明当x≥0时,f(x)≥0恒成立.
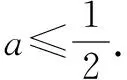
说明:本题先利用定理得到f(x)≥0成立的必要条件,然后再证明其充分性.
例2 当x≥0时,ax2+1≤xex+e-x恒成立,求a的取值范围.
解ax2+1≤xex+e-x⟺ax2+1-xex-e-x≤0.
令f(x)=ax2+1-xex-e-x,
则f(0)=0.
f′(x)=2ax+e-x-ex(x+1),
∴f′(0)=0.
f″(x)=2a-e-x-ex(x+2),
令f″(0)=2a-3≤0,
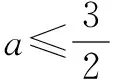
又f′(0)=0,则y=f′(x)在x≥0时有f′(x)≤0,则y=f(x)在x≥0时单调递减,又f(0)=0,从而说明当x≥0时,f(x)≤0恒成立,即当x≥0时ax2+1≤xex+e-x.