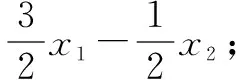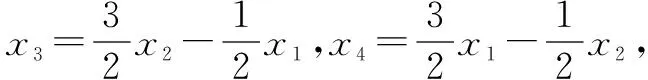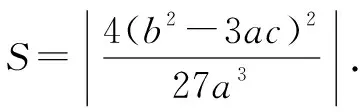三次函数极值点特征分析
姜勇钢
(江苏省南通市海门第一中学 226100)
笔者借助本文,通过一道三次函数为原型题目的分析、解答、求解、归类等,将一题的多种方法一一呈现,并通过题目的分析引领学生去深入分析、感悟题目,学会在对比中感悟,在感悟中应用,在应用中提升,在长期的教学引领下,实现减负高效的数学学习环境.
一、例题呈现
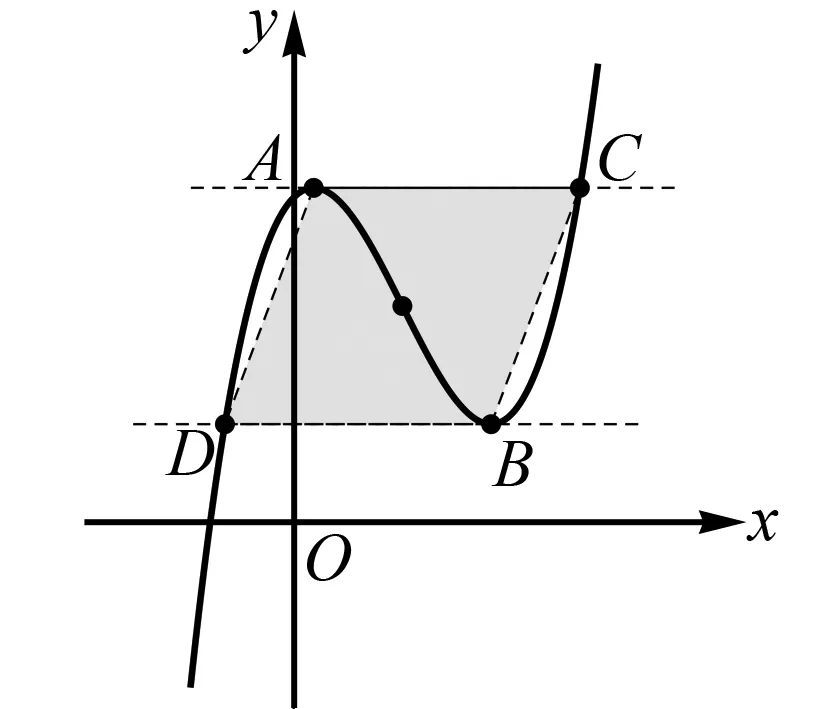
已知f(x)=x3+ax2+bx(a,b∈R),若函数f(x)有两个极值点x1,x2,x1 方法一(直接代数运算)求导得 f′(x)=3x2+2ax+b, 所以x1,x2是方程 3x2+2ax+b=0 的两个根,根据韦达定理得 又由题意得 所以g(x)=f(x)-f(x0) =(x-x0)(x-x1)2 显然它有两个零点,分别为x1和x0. 方法二(平移代换)将f(x)的解析式作如下变形: ① ② 而g(x)=f(x)-f(x0)=[φ(t)+B]-[φ(t0)+B]=φ(t)-φ(t0). ③ 所以原题等价于下列命题: 已知φ(t)=t3+At,若函数φ(t)有两个极值点t1,t2,t1 显然有两个零点t0,t1. 方法总结,并引领学生进行全面的解读和反思,这是全面提升这道题目的价值所在,也是提升学生解题能力的关键所在,在这道题目上,我们可以做以下四个环节的总结与反思,分析与提炼、变式与拓展. 1. 判断一个多项式的零点时,如果能因式分解,当然优先考虑因式分解. 在本题中,显然有一个零点是x0,所以必有一个因式x-x0. 而这道题选择作为参数x1,x2,消去a,b,x0,而不是通常地利用韦达定理转化以a,b为参数,是因为x0的表达式中x1,x2的地位并不对等,无法凑出只含x1+x2和x1x2的形式. 2. 本题可以推广至一般情况,得到下列结论: 设三次函数f(x)=ax3+bx2+cx+d(a≠0)有两个极值点x1,x2,且x1 图1 即点A在线段DB上的投影将线段DB分成1∶2的两部分,点B在线段AC上的投影将线段AC分成2∶1的两部分. 3.2016年天津高考压轴题第(2)问即以命题为背景,求证A,F,C(D,F,B)横坐标之间的关系. 现节选如下: (文)设函数f(x)=x3-ax-b,x∈R,其中a,b∈R,若f(x)存在极值点,且f(x1)=f(x0),其中x1≠x0, 求证:x1+2x0=0; (理)设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R,若f(x)存在极值点,且f(x1)=f(x0),其中x1≠x0,求证:x1+2x0=3. 4. 2013年广东文数压轴题第(2)问亦与此有关,节选如下: 设函数f(x)=x3-kx2+x,当k<0时,求f(x)在[k,-k]上的最小值m和最大值M. 容易分析得该三次函数在[k,-k]上的图像包括了DABC,所以最小值在左端点取得,最大值在右端点取得.而将函数与端点函数值作差,代数变形后判断符号即可说明这一点: f(x)-f(k)=(x3-kx2+x)-k=(x-k)(x2+1)≥0 以及f(x)-f(-k)=(x3-kx2+x)-(-2k3-k)=x3-kx2+2k3+x+k=x2(x+k)+2k(k2-x2)+(x+k)≤0. 易得m=f(k)=k,M=f(-k)=-2k3-k. 5. 平移代换是简化问题的常用技巧,如上面的2016年天津高考题,经过平移代换之后,两个命题是完全等价的,但是文科的题从面上看确实比理科题简单,若我们能以运动的观点来看函数图像,不拘泥于表达式这件“外衣”,想必我们能更快地抓到问题的本质. 授之以鱼不如授之以渔,在常态的课堂教学过程中,我们要致力于教育教学质量的训练和提升,这就要求我们站在学生的高度,帮助学生去剖析相应问题的本质,举一反三、一题多解、一题多变,在深入的研究中触发学生的能力生长.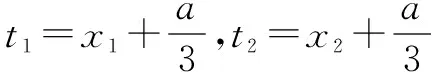

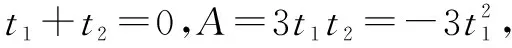
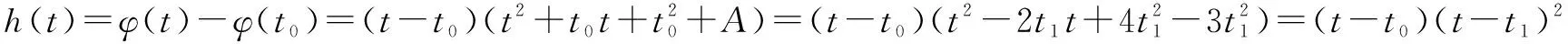
二、方法总结