一道清华大学能力测试题的探究

江苏省盱眙中学 (211700) 陈海波

一、试题呈现

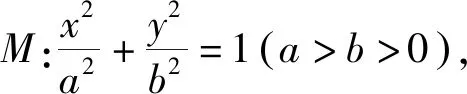
(1)求椭圆M的方程；

(2)设O为坐标原点，A,B,C是椭圆上不同的三点，并且O为△ABC的重心，试求△ABC的面积.

本题是2018清华大学THUSAAT测试题理科第20题，第(1)问考查了椭圆标准方程的求解方法，考查了待定系数法，运用了方程思想，化归与转化的思想；第(2)问考查椭圆内接三角形面积的定值问题，基本涵盖了解析几何中三角形面积问题的基本方法.构思精心，巧妙，入口宽广，解法多样，有好的区分度，为不同学生能力的施展提供了一个非常好的平台，要求学生有一定的分析问题和解决问题的能力，同时本题第2问内涵非常丰富，还可以进行深度的挖掘和推广.

二、解法探究

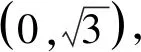
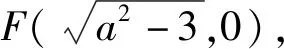
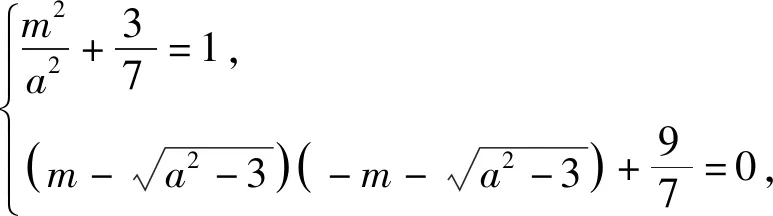
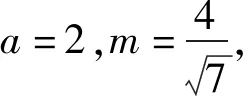
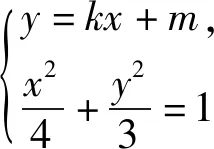
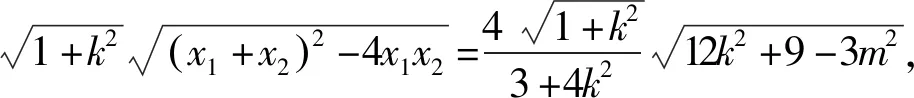
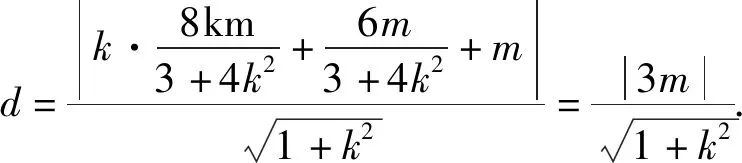
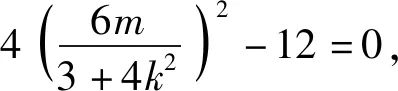
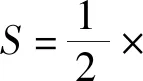
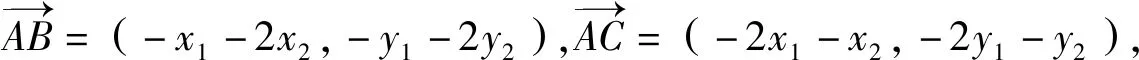
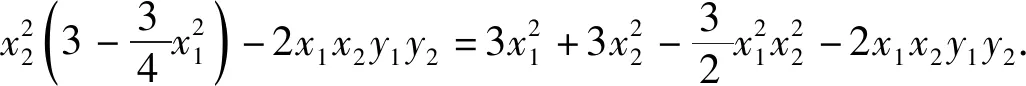
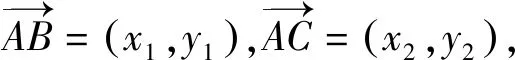
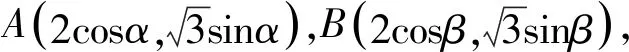
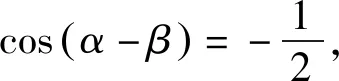
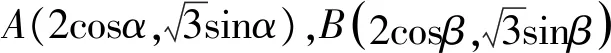
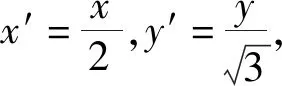
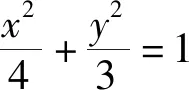
三、变式探究

波利亚说“好的问题如同某种蘑菇，有些相似，它们大都成堆地生长，找到一个以后，你应该在周围再找找，很可能附近就有几个” .本题中，可以发现如下变式：

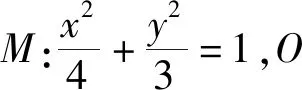
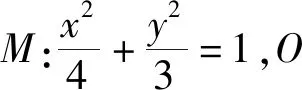
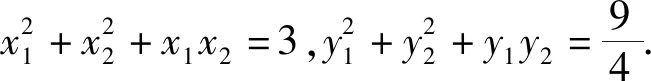
四 、一般性结论

从特殊对象推广到一般性结论是数学发现和数学创造的常见方法，也是数学研究常用策略，本题中的结论还可进行一般形性的推广得如下结论：

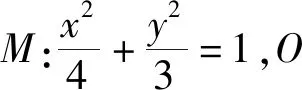
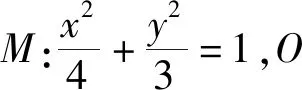
五、习题链接

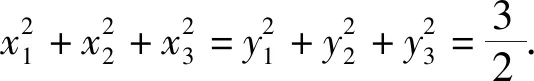
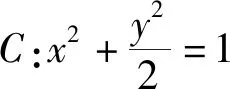
(1)证明：点P在C上；

(2)设点P关于点O的对称点为Q，证明：A,P,B,Q四点在同一圆上．

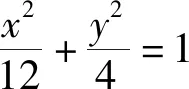
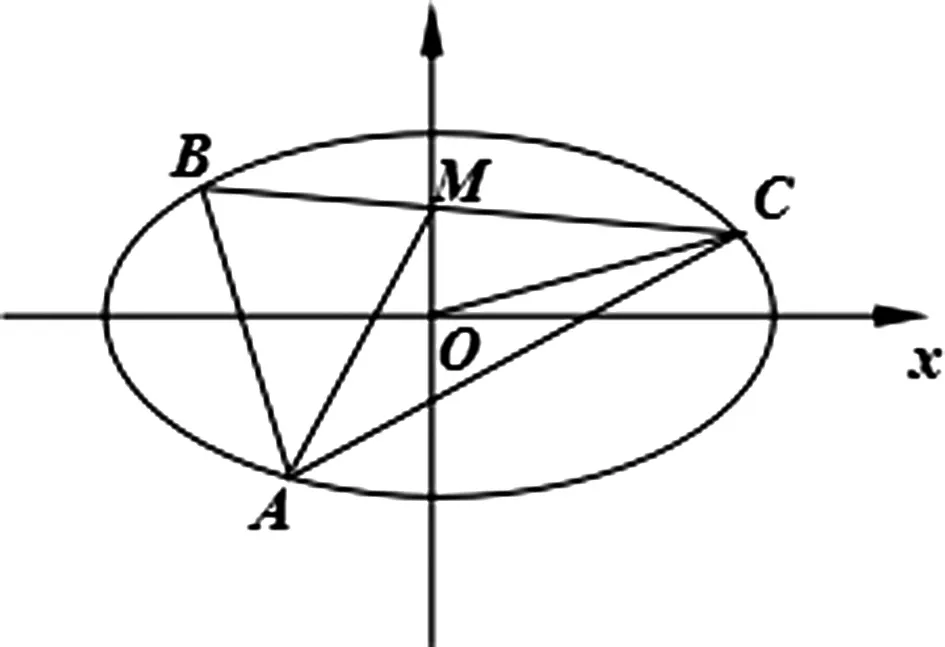
图1

六 、结语

本题既具选拔功能，也凝聚了命题者的数学素养，具有立意高远，背景深刻的特点，通过研究可以体会到其中丰富的数学思想及数学深层次的联系.