土壤重金属空间含量预测的几种分析方法

张钊熔 ，石海兰

（1.自然资源部退化及未利用土地整治工程重点实验室，陕西 西安 710021；2.陕西地建土地工程技术研究院有限责任公司，陕西 西安710021；3.陕西省土地工程建设集团有限责任公司，陕西 西安 710075；4.陕西省土地整治工程技术研究中心，陕西 西安 710021）

受自然来源和人为活动引起的土壤重金属污染由于污染面积扩大、危害加剧等成为一个全球性污染问题。因此，土壤重金属污染的现状、来源和修复受到了各国学者、相关环保机构以及政府和民众的密切关注[1-3]。近些年来，我国政府多次主导国内土壤污染状况调查（全国土壤污染状况调查，土壤地球化学调查等），调查结果表明，作为土壤污染物的重金属污染已经严重影响了部分地区的土壤安全，对当地农作物和居民身体健康有着极大的危害[4-5]。重金属作为污染物进入土壤，不能由自然环境的自净能力去除，只能在土壤介质的条件下由一种重金属化合物转变为另一种重金属化合物或受土壤溶液的影响在水平或垂直方向迁移。因此，土壤中的重金属污染物在自然环境的条件下不能有效地去除，对生态环境的危害具有长久性。农田中的重金属污染物可以通过作物种植时的根系间作用进入到作物体内，自农作物根部向地上部分运移，最后在作物可食用器官累积，对粮食的安全生产造成隐患。当人食用重金属污染的粮食和环境暴露等途径将重金属摄入体内，将引起人体重金属中毒[6]。因此对土壤重金属污染的空间分布特征进行研究，是了解土壤重金属污染和着手修复治理的前提。现今对土壤重金属污染空间分布特征的研究是通过实地调查取样、室内化验。但是由于经费、样品代表性、采样方式等原因，所得的土壤重金属含量数据出现是否有代表性、且数据不连续等问题，这必然影响土壤重金属污染物的实际空间分布与模型拟合间的准确性。因此，土壤重金属的空间分布含量预测及影响因素一直是国内外环境学者研究的热点问题[7-9]。现今土壤重金属污染物含量预测不再仅仅是定性地研究土壤重金属含量分布特征，而是定性与定量建模相结合的系统性研究。首先，这一研究方法能对空间上土壤重金属含量得到较准确的预测。其次，通过一段时间内的多次采样监测，也能够对未来某一阶段或某一时间点的重金属含量作出预测[10]。较为准确的土壤重金属含量分布模型能够让研究者和相关工作者了解该地区土壤重金属含量变化及其主要影响因素，这对区域土地合理规划、土壤修复治理、农业生产管理等问题具有重要的参考价值。

现阶段对土壤重金属含量预测的研究方法主要有两类：一是遥感高光谱反演[11-12]；二是通过土壤理化性质（土壤粒级、pH值、腐殖值、有机碳含量）、污染源方向、污染源距离、地面坡度等条件下的反演[13-14]。这两种技术的理论方法是相似的，遥感光谱反演是将含重金属的土壤光谱与高光谱遥感获得的土壤光谱信息通过建模拟合联系起来；土壤理化性质、污染源方向、坡度等条件下的反演同样是在同一样点将这些因素与土壤重金属含量通过建模或者算法拟合联系起来。两种方法最终都是通过这种联系来预测反演其他点位的土壤重金属含量。对于这两个方向的学者做了很多研究[15-17]，本论文主要综述几种通过土壤理化性质等条件下的土壤重金属含量预测模型或算法，讨论模型间的优缺点和适应性，以期推动土壤重金属空间分布模型在土壤重金属分布特征中的研究与实践应用。

1 模型与应用

1.1 多元线性回归模型

多元线性回归是一种传统的统计学方法，可以同时综合多个变量，从多元数据中获取信息。在实际应用中，某一事物的变化总是由多种因素共同影响的结果，为了明确这些影响因子对这一事物的影响权重以及通过这些因子来预测事物发展变化，进而引入了多元线性这一统计分析方法理论。多元线性回归模型是研究一个因变量和多个自变量之间关系的理论和方法[18-20]。多元线性回归模型的构建，有未标准化和标准化两个模式。未标准化回归模型是使用原始数据的回归模型。在其他因素保持不变的情况下，它能切实反映自变量每变化一个单位对因变量的影响程度。由未标准化回归模式建立的模型，可以直接对因变量进行预测得出结论。标准化回归系数是将自变量和因变量的数据消除量纲、数量级等处理后，构建的回归模型。使得不同变量间的关系清晰，可相互对比，进而确定自变量对因变量的影响大小。标准化回归系数的绝对值越大，则认为对因变量的影响就越大。

多元线性回归模型已频繁应用于土壤重金属空间分布研究，根据其理论，多元线性回归不仅能构建土壤重金属预测的回归方程，同样能确定影响土壤重金属含量的几种因素间的相对重要程度。早在1989年，胡永定就开始使用多元线性回归来预测土壤中的重金属含量[21]。近些年来，这一方面的研究也越来越多，同时也有学者着重于多元线性回归对土壤重金属来源分析。Zeinab Salim等人在巴基斯坦喜马拉雅山麓采样主成分和多元线性回归分析了对道路灰尘、土壤和植被中的重金属来源，认为主要来源为长距离的大气输送、湿沉降、母岩释放、车辆排放以及其他大气来源[22]。Zhao等人采用主成分分析和线性回归分析了公园粉尘中的Pb来源，其主要来源于煤燃烧、土壤母质和施肥以及交通，各项来源占比与Pb同位素示踪来源占比相吻合[23]。

1.2 空间回归模型

为了满足具有空间属性的数据处理分析，1981年，空间自回归模型建立。目前，该模型已经开始应用于具有空间属性数据的多个研究领域[24-26]。空间回归模型将分析中的假设（独立性、随机性）弱化，然后进行求解加入空间距离，根据空间距离来加权，距离越近权重越高。

空间回归模型的一般形式为[27]：

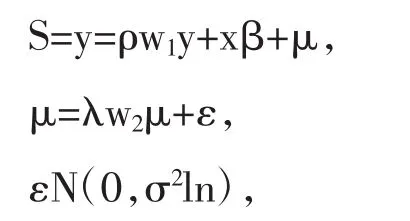
式中：y为因变量；x为自变量;β为自变量x相关的参数向量；ρ为空间滞后项w1y的系数；λ为空间误差项的回归系数；w1、w2为与因变量和残差的空间自回归过程相关的权重矩阵；ln为残差的空间自相关系数。

空间回归模型有三种OLS、SLM、SEM。OLS（普通线性回归模型）：由于OLS不考虑空间上相邻区域变量的互相影响，w1、w2前面的系数 ρ、λ 都为 0。

SEM（空间误差模型）：系数 ρ=0，λ≠0；表明某一空间对象上的因变量与同一对象上的自变量有关，还与相邻对象的自变量、因变量有关。

SLM（空间滞后模型）：系数 ρ≠0，λ=0，空间滞后模型是考虑因变量的空间相关性。即，某一空间对象上的因变量不仅与同一对象上的自变量有关，还与相邻对象的因变量有关，通常把变量的前期值，即带有滞后作用的变量称为滞后变量，滞后变量分为滞后解释变量与滞后被解释变量[28]。

霍霄妮等人研究认为空间自回归模型能够很好地解释重金属含量与其影响因素间的相关关系[29]。Wu等人研究认为空间滞后模型优于多层线性回归模型。空间滞后项的显著系数表明Pb和Cd的空间变化依赖于它们周围的观测。研究结果强调了重金属的空间自相关性，以及内在因素和环境变量对这些金属空间变化的影响，揭示了空间回归模型在识别重金属影响因素方面的有效性[30]。

1.3 人工神经网络模型

构建理念源自生物神经网络的人工神经网络（神经网、连接模型）[31]，由神经元、节点之间的权重等结构组成。每个节点都有相对应的函数称为激励函数。任意两节点之间的连接都可以通过信号的加权值（也称为权重）完成[32]。神经网络上层的神经元通过传递函数与下层神经元连接，同层神经元之间没有连接，学习样本提供给神经网络后，神经网络首先进行正向传播。如果输出结果与目标值的误差超出预期，则正向传播过程转为反向传播过程，误差信号沿原链路返回。通过改变每一层神经元的权重来减少误差，这种误差反向传播修正不断进行，网络对输入模式的响应精度不断提高，最终达到适用的精度[33]。神经网络因此具有学习、统计、归纳等能力。换言之，通过数理统计神经网络能够像人类一样进行简单判断，这比现代一些逻辑推理运算更准确[34]。

人工神经网络已经频繁应用于环境生态污染研究中，侯艺璇等用BP神经网络预测模型对小麦、水稻、油菜籽及蔬菜可食部分Cd含量预测，划分得到4种作物适宜种植区[35]。Ihuaku Anagu等认为神经网络模型能够较好地以土壤基本性质来估算土壤重金属吸附[36]。秦夕淳在土壤Cd含量预测研究中发现，不同参数和不同模型下，神经网络的预测结果是不同的[37]。樊宁将BP神经网络与情景分析法相结合对燃煤电厂周边土壤重金属含量进行未来预测，预测精度较高[38]。

2 讨论与总结

多元线性回归在土壤重金属含量的预测，可以先将影响因素标准化，确定各影响因素影响力占比，然后使用未标准的回归系数，做多元回归方程，对回归方程进行检验，从而对因变量预测。但是采用传统回归模型来进行土壤重金属含量及其影响因素间相关关系的分析，该方法的理论假设前提是数据本身在统计上是独立的且均匀分布[39]，而土壤重金属含量作为空间数据的一种往往具有一定的空间依赖关系，即空间性，若采用传统的回归模型，通常会忽略空间相关的影响而产生偏差[29]。空间回归可更好地解释地理事物的空间关系。土壤空间位置与各种重金属的含量之间，以及污染程度与不同重金属含量之间均存在高度复杂的非线性映射关系[40]。神经网络可以综合考虑土壤环境质量模糊性及各污染因素的权重，循环地对权重值进行调整，使输出误差平方和达到最小值，使得计算预测结果更具科学性[41-42]。

现今土壤重金属含量空间预测研究模型多样，还有一些其他方法理论，例如：空间数据分析（ESDA）、地统计学及空间插值分析、空间随机模拟等。各种不同模型对土壤重金属空间含量的预测精确性是不同的，故而今后可能在需要对比不同的土壤重金属含量预测模型来探讨各模型的优劣性。其次，算法模型并不是一成不变的，可以收集前人经验结合自己的学识对模型进行改良和创新。