基于同态加密的DBSCAN 聚类隐私保护方案

贾春福，李瑞琪，王雅飞

（1.南开大学网络空间安全学院，天津 300350；2.天津市网络与数据安全技术重点实验室，天津 300350）

1 引言

云服务的快速发展，为用户提供了更加多元化的数据处理方式。用户可以选择将数据集上传到云服务器，由云服务器执行相关操作，从而减少用户计算资源的使用。由于用户种类繁多，其提供的数据集也将涵盖多种类型，比如电子邮件信息、后台用户数据库信息、个人健康状况等涉及个人隐私或企业商业机密的信息。用户将上述信息进行外包处理时，其中包含的敏感信息存在着泄露的风险。因此，如何对敏感数据所包含的隐私进行保护是当前的研究热点。

隐私保护常见的处理方式主要有2 种：一种是通过硬件或可信第三方提供的可信信道来保证传输过程中的数据不被窃取；另一种是将数据加密后进行传输，即使攻击者获得密文，没有密钥也无法进行解密。第一种方式虽然可以保证传输过程中的安全性，但其对第三方有较大依赖；并且，由于其使用明文传输，当数据集传输到云服务器端后，仍然存在着被窃取的风险。第二种方式将数据集加密后传输，这样无论在传输过程中还是在服务器端计算过程中都能够保证数据明文不会被泄露。

对数据集进行加密时，如果使用传统的加密算法，服务器无法直接对密态数据进行处理，需要用户向服务器提供密钥或执行解密操作。同态加密（HE,homomorphic encryption）是一种新型密码学工具，其支持在加密信息上进行任意函数运算，并且解密后得到的结果与在明文上执行相应运算的结果一致。同态加密算法依照所支持的运算种类和次数不同，可大致分为以下几类：支持无限次数和多种运算的全同态加密（FHE,fully homomorphic encryption）算法、支持无限次数和有限种类的部分同态加密（PHE,partial homomorphic encryption）算法、支持有限次数和多种运算的浅同态加密（SWHE,somewhat homomorphic encryption）算法[1-4]。大部分应用场景只需要有限次同态加法或乘法操作，并且SWHE 算法相较于FHE 算法而言具有更好的效率，因此SWHE 算法具有更加广泛的应用场景[5]。BGV（Brakerski-Gentry-Vaikuntanathan）方案是一种常用的SWHE 算法，支持加密多项式或整数，同时也可以利用中国剩余定理实现并行化操作。

同态加密同时满足保密性和密文可操作性的特点使其在隐私保护领域有较广泛的应用。基于同态加密的外包计算的隐私保护模型如图1 所示。用户对需要外包的数据集进行加密，并上传到服务器端（①），由服务器进行较高计算复杂度的数据处理；然后，服务器将结果返回给用户（②）。

机器学习是一种重要的数据外包计算，其隐私保护问题是同态加密的一类重要应用场景。在过去几年中，研究者针对不同的应用场景、不同的数据类型以及不同的机器学习算法，开展了许多同态加密在机器学习隐私保护中应用的工作。文献[6]实现了高效且安全的k 近邻（kNN，k-nearest neighbor）算法。文献[7-8]实现了加密数据集上的同态K-means 聚类算法，但其存在时间开销较大的问题。文献[9-11]的加密对象是图片，其对图片型数据集执行加密操作后，在密态图片上提取特征，并应用不同的图像匹配算法，实现密态图片的匹配。文献[12]实现了密态数据集上的统计学习算法。文献[13-14]通过逐比特运算的方式实现了加密数据集上的比较算法或协议，但其开销较大。文献[15]预先在数字型数据集上提取相关特征，然后将特征加密后上传到云端，在云端对相关特征的密文进行同态运算后，完成分类运算。本文提出的方案与之不同，加密对象为原数据集，而后在云端执行同态聚类操作。

图1 基于同态加密的外包计算的隐私保护模型

常见的机器学习算法主要分为有监督型和无监督型。有监督型机器学习算法能够提取训练数据集的特征和真实标签以构建模型，并对测试数据进行测试从而得出相应结果，代表算法有贝叶斯分类器、超平面分类器、决策树分类器等；无监督型机器学习算法不需要预先训练模型，代表算法主要有K-means 聚类算法、DBSCAN（density-based spatial clustering of application with noise）算法等。DBSCAN 是一种基于密度的无监督型机器学习聚类算法，能够在有噪声点的情况下找到任意形状的聚类簇，相较于另一个常见的聚类算法K-means，其应用范围更加广泛，如可用于推荐系统等高级系统的实现。DBSCAN 还可用于与加速范围访问（如R*−树）相配合的一种数据库结构的设计。因此，DBSCAN 隐私保护问题的研究具有重要意义。

本文提出了一个基于同态加密的聚类学习的隐私保护方案，实现了在密文数据集上进行同态DBSCAN 的聚类操作。因为BGV 同态加密算法计算效率较高、明文空间选择灵活，所以本文选择其对数据进行加密。为了解决BGV 算法不能直接加密浮点型数据的问题，本文提出了3 种不同的浮点型数据预处理方式，根据浮点型数据集自身特点、综合考虑计算开销和数据精度进行选择。对于同态加密不支持的密文比较运算，本文设计了一个云服务器与用户之间的协议实现密文的比较操作，协议只涉及同态密文之间的加减法操作，计算复杂度较低。

2 基础知识

2.1 符号介绍

对于一个实数z，分别表示对z向上、向下和就近取整；[z]m表示zmodm。使用小写粗体字母表示向量；大写字母X={x1,x2,…,xi}表示集合，表示集合中元素的个数；大写粗体字母表示矩阵（如A），AT表示矩阵的转置。符号←表示随机选取；R表示环，Rq=R/qR。对于明文空间中的元素m∈M，符号〚m〛表示其密文。

2.2 同态加密算法

定义1 同态加密。同态加密算法主要包含4 个部分：密钥生成（KeyGen）、加密（Enc）、密文运算（Eval）、解密（Dec）。

①(pk,sk)←KeyGen(λ)：输入安全参数λ，输出公钥pk 和私钥sk。

②c←Enc(pk,m)：输入消息明文m∈M 和公钥pk，输出密文c。

③m←Dec(sk,c)：输入密文c和私钥sk，输出消息明文m。

④cEval←Eval(C,{c1,…,ck},pk)：输入一个布尔电路C、一组密文 {c1,…,ck}和公钥pk，输出结果密文cEval。

本文选取文献[2]提出的BGV 方案，并借助于同态加密算法库HElib 完成方案的实现。BGV 方案包括以下几个算法。

Setup(1λ,1μ)。随机选取μbit 的模数q，选取n=n(λ)，N=N(λ)，χ=χ(λ)，t=t(λ)，d=d(λ)。令R=Z[x]/f(x)，其中f(x)是n次分圆多项式。上述参数的选取应保证方案的困难性能够基于格困难问题GLWE（general learning with error），并能够抵御现有攻击。

KeyGen(λ)。选取s←χd，令私钥为sk=。随机抽取矩阵，向量e←χN，计算b←As+te，令公钥为B=[b,−A]。显然，Bs=te。

Enc(pk,m)。将明文m∈Rt扩展成m←(m,0,…,0)∈，随机选取，输出密文

Dec(sk,c)。输出

Eval (c1,c2)。密文加法输出c12，密文乘法输出c12。

HElib 中除了上述算法之外还包括一些用于实现FHE 算法的处理程序[16]，例如key switching、modulus switching 和bootstrapping。FHE 算法存在密钥过长、密文量级过大、降噪处理耗时较长等弊端，在实际应用中具有一定的局限性；SWHE 算法虽然不支持无限次密文运算，但其密文和密钥的尺寸较小，也不需要bootstrapping 技术对密文进行刷新，因而运行效率较高。由于本文的场景只需有限次密文运算，因此选择使用SWHE 算法，以获得较高的计算效率。

2.3 数据预处理算法

大多数实际应用中的数据都不能够直接作为加密算法的明文，需要一定的预处理算法将实际数据映射到明文空间。本文所研究的DBSCAN 算法需处理的数据是浮点型数据集，所以需要使用预处理算法将其映射至加密算法的明文空间。本节将介绍3 种数据预处理方式。

方式1整数对编码

设原数据为浮点数c，选取整数a和b使b=a×c，则使用数对(a,b)表示数c。例如：1.5可使用数对(2,3)表示；1.2 可使用数对(2,2)、(5,6)等表示。选取数对时应综合考虑时间开销和精度要求。

方式2移位舍入编码

设原数据为c.d，其中c为整数部分，d为小数部分，且c与d位数基本相同。将原数据c.d的小数点后移v位，得到新的数据cd'。

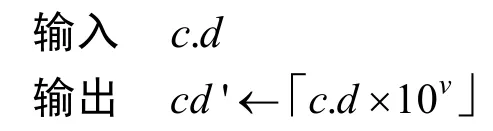
这种处理方式相当于将原有数据扩大了10v倍，然后根据实际要求，对扩大后数据的小数部分进行适当的舍入，从而既能够保证该类型数据的精度，又不需要在加密时选取较大的加密方案参数。

方式3多元处理编码

原数据c.d如方式2 描述，且c与d的位数均小于加密算法所能处理的最大位数。

输入c.d

输出(c,d)

将原数据的整数部分c和小数部分d拆分为二元组(c,d)。

这种处理方式最具有普适性，能够完全保证数据精度不会因预处理操作而受到损失，然而这种处理方式也存在一定的弊端。用户若使用方式3 将原数据变为二元组，则数据量变为原来的两倍，从而增加加密阶段的开销。除此之外，在执行同态乘法操作时，由原来一对整数相乘变为两对整数相乘，乘法次数增加，计算复杂度增加。

在实际应用过程中，根据所需处理的数据精度，可以选取上述3 种预处理方式中的一种，也可以选取多种预处理方式结合使用，使效率与精度之间保持平衡。与此同时，针对选取的同态加密算法不同，其明文空间的类型和容错能力也不相同的情况，在选取具体预处理方式时，也应当考虑预处理方式对后续同态加密计算开销等方面的影响。

2.4 DBSCAN 算法

DBSCAN 算法是一种常见的聚类算法，用来在数据集中构建聚类簇并发现噪声数据[17-18]。相较于同样常见的K-means 聚类算法，DBSCAN 算法不需要预先定义数据簇的个数，并且适用于任何形状的聚类簇的构建，甚至是无连接的环状聚类簇。由于存在最少点数的限制，相较于K-means 算法，DBSCAN 算法可以避免single-link 影响，因此对于任意形状的数据分布，DBSCAN 算法都具有较好的聚类效果。

DBSCAN 算法本身也有很多变形，原始的DBSCAN 算法复杂度为Ο(n2)，ρ-近似DBSCAN算法复杂度为Ο(n)，但是其对数据的维度有一些限制。DBSCAN 算法的选取与数据类型相关，根据本文方案数据集的数据类型，选取二维DBSCAN 算法完成相关实验。

DBSCAN 算法的一些概念定义如下。MinPts 定义了一个聚类簇所需的最少数据点数，ε-邻域表示以某个点为中心点，并以其为圆心、以ε为半径的圆所覆盖的范围。中心点，即聚类簇的中心，其ε-邻域中包含的数据点比MinPts 多；边缘点，即在聚类簇边缘的节点，其ε-邻域中包含的数据点比MinPts 少，并且其在其他中心点的ε-邻域中；噪声点，即数据集中非中心点和边缘点的其他数据点。节点定义的实例化描述如图2 所示。除此之外，定义2 和定义3 给出了密度可达和密度相连的定义。

图2 节点定义的实例化描述

定义2密度可达。令xi,xj为2 个数据点。设存在样本序列p1,p2,…,pn，其中p1，pn=xj，若对于1≤k≤n，都有pk+1在以pk为中心点的ε-邻域中，则称xj由xi密度可达。

定义3密度相连。对于数据点xi,xj，如果存在一个点xk，使通过xk后xi与xj是密度可达的，则称xj与xi密度相连。

DBSCAN 算法的流程如下。

步骤1输入数据集合。选择一个未被标记过的观察点xI作为当前节点，标记第一个聚类簇1。

步骤2找出以xI为中心点的ε-邻域内的所有节点，其均为xI的邻居节点。执行下述操作。

①若找到的邻居节点数目少于MinPts，则xI是一个噪声点，执行步骤4。

②若找到的邻居节点数目不少于MinPts，则xI是一个中心点，执行步骤3。

步骤3分别将所有邻居节点作为中心点，重复步骤2，直到没有新的邻居节点可以作为中心点。

步骤4从数据集X中选择下一个没有被标记的点作为当前节点，将聚类簇的数目更新并加1。

步骤5重复步骤2～步骤4，直到数据集X中的所有点都被标记。

2.5 方案的评估标准

方案的评估标准包括2 个方面：时间效率和准确率。

时间方面，本文关注的是云端执行同态DBSCAN 算法的时间。除了时间的评估外，另一个重要的评估标准是聚类的准确率。根据DBSCAN算法的特点，准确率的评估标准包含聚类簇数量和噪声点判断。本文将对比直接在明文上进行DBSCAN 算法所得结果和在密文上同态执行DBSCAN 算法解密后得到的结果。聚类的准确率定义为2 次聚类结果中相同结果的占比，最理想状态为2 次结果完全相同。

3 DBSCAN 隐私保护方案

本文构建了一个在加密数据集上的同态聚类算法，从而实现在外包计算过程中敏感数据集的隐私保护。根据同态加密算法所支持的运算方式，可以将DBSCAN 算法中的运算划分成2 类：同态加密算法支持的运算和同态加密不支持的运算。对于同态加密不支持的运算，可以通过设计协议的方式来进行处理，从而实现加密数据集上的同态聚类功能。同态DBSCAN 算法如算法1 所示。

常见的同态加密方案仅能支持加法（减法）、乘法运算，所以复杂运算需要进行相应的转换使其能够用加法和乘法表示。算法1 的步骤3)中的函数所涉及的运算并不能够完全被同态加密算法所支持。不支持的运算有以下2 种。

1)在计算〚ε〛-邻域时，需要计算点与点之间的距离，最常用的是欧氏距离，但其中所涉及的开方运算并不被同态加密算法支持。

2)本文所选取的同态加密方案不具备保序加密的性质，加密后的密文之间不会保持原有明文间的大小关系，故需解决密文大小比较问题。

上述2 个问题的解决方式将分别在3.2 节和3.3节中进行介绍。

3.1 数据集预处理

本节首先给出一种基于数据特点，结合精度和计算开销等条件的选取数据预处理方式的方法，选取流程如图3 所示。

图3 预处理方式的选取流程

设需处理的数据集为X={x1,x2,…,xn}，数据整数部分的位数为p，小数部分的位数为q（有效位数不足时用0 补齐）。从X中选取较大的数xi和较小的数xj，计算的值，判断此绝对值是否满足＜ς，其中ς为用户根据数据集的特点自行设定的阈值。若满足（即数值相差较小），则直接选用多元处理编码方式以保证数据精度（此种情况说明集合中的数值大小差异主要在小数部分）；若不满足，则进一步判断是否满足q−p＞η，其中η为用户根据情况自主设定的阈值。若q−p＞η，则将小数部分的较低位舍去（大约舍去q−p位），即小数部分的位数由q变为q′（使q′≈p）；否则直接跳转到下一步判断。此时，需要综合考虑保留精度和后续计算开销问题来判断是选择整数对编码方式还是移位舍入编码方式：若此时的数据精度的损失对后续计算结果影响较大，为提高计算精度，则选择整数对编码方式；若数据精度的损失对后续计算结果影响较小，则选择移位舍入编码方式。

本文方案中需要保护的敏感信息是每条数据的坐标值，是浮点型数据，因此需要根据数据集的特点以及本文方案所选用的加密方案来选择适合的预处理算法。本文方案选取了2 个浮点型数据集A、B，A 中数据的小数点后位数较多，但其数值大小的差异较大，且小数位数远大于整数位数，故根据图3 所示的选取流程，可以考虑采用整数对编码方式或移位舍入编码方式，并且对小数部分进行舍去，本文方案中分别保留了3、4、5 位小数进行后续实验。B 中数据间差异较大且小数位数与整数位数相差不大，因此根据上文所述的选取方法，也可以考虑使用整数对编码方式或移位舍入编码方式。使用整数对编码方式处理数据后的加密过程如图4 所示。

图4 使用整数对编码方式处理数据后的加密过程

从图4 中可以看出，一个数据经方式1 处理后会转换成一个二元组进行加密，后续的密文操作也会增多，从而计算开销会变大，但整数对编码方式能够尽可能地保留当前数据的精度。移位舍入编码方式则会造成一定程度的数据精度损失，但相较于整数对编码方式计算开销会更低。因此，可以通过实验来观测数据精度的损失对A、B 这2 个数据集聚类结果的影响，从而决定使用哪种预处理方式是更合适的（实验结果见4.1 节）。本文方案选取的加密算法的明文空间是有限比特长度的整数集，因此预处理后的数据可以直接进行加密。

3.2 距离测度选取

在机器学习算法中，常用的距离测度包括欧氏距离、曼哈顿距离、变形欧氏距离等。相较于传统欧氏距离，变形欧氏距离能更进一步保留数据的精度，降低由开方舍入造成的误差影响。

定义4变形欧氏距离。现有2 个点a(x1,y1)与b(x2,y2)，变形欧氏距离可表示为

在进行距离比较时，欧氏距离和变形欧氏距离具有较高的准确性，曼哈顿距离有一定的误差。然而，欧氏距离中的开方运算不被同态加密算法支持，需要对开方运算进行进一步处理。文献[19]中使用了牛顿迭代的方法进行同态开方运算，过程如下。

定理1牛顿迭代开方。若方程x2−t=0，其中t为实数，则在x0附近存在一个根，使用迭代公式

依次计算x1,x2,…，序列将无限逼近方程的根。

如定理1 所示，牛顿迭代法可将开方运算转换为基础运算，从而满足同态加密方案的要求。这种解决方法虽然可以实现开方运算，但式(2)涉及的所有常数均需提前进行加密处理，并且在运算过程中涉及多次密文乘法运算，计算复杂度较高。除此之外，牛顿迭代法所得结果是近似结果，会有一定的误差，此误差可能会给聚类结果造成较大影响。

定理2令a和b为2 个整数，设a的比特长度为l1，b的比特长度为l2，那么有ab的比特长度不大于l1+l2，的比特长度不大于(l1+l2)/2。

如定理2 所示，使用变形欧氏距离所得结果的比特长度为欧氏距离结果的两倍。虽然这会导致在后续计算过程中数据规模变大，从而使计算时间略有上升，但变形欧氏距离的计算过程仅需2 次乘法，相较于牛顿迭代法（为了保证开方结果的精度，需要迭代多次，从而需要多次乘法），比特长度增长所带来的额外开销相对较低。

与此同时，本文进行了距离测度对聚类准确度影响的测试。一般情况下，聚类算法中使用的距离测度是欧氏距离，因此测试的主要方式是将欧氏距离分别替换成曼哈顿距离和变形欧氏距离后观察聚类结果是否与使用欧氏距离时的聚类结果相近。选取同样的输入参数，使用这3 种距离测度在明文上进行聚类，得到的结果如图5 所示。其中，横纵坐标为数据点的值，相同颜色为同一聚类簇，不同颜色为不同聚类簇，边缘深色数据点为噪声点。图5 中的3 幅图分别表示选择欧氏距离、曼哈顿距离和变形欧氏距离的聚类结果。由图5 可知，欧氏距离和变形欧氏距离的聚类结果类似，而曼哈顿距离相较于欧氏距离的聚类结果有一定误差。结合上述分析与实验结果，同时考虑数据集精度和后续同态运算的开销，本文方案采用变形欧氏距离。

图5 数据集A 不同距离测度聚类结果

3.3 密文比较协议

用户端与服务器端的交互场景如图6 所示。服务器将需要解密的密文发送给用户，用户解密密文后将解密结果的最高位发回给服务器。在此过程中，用户与服务器可以协商设置一个时间段t，每隔t时间，用户向服务器发起询问，服务器依据运算进程返回需解密的中间结果或同态聚类结果。在这种情形下，用户不需要一直在线等待，只需间隔一段时间发起询问即可。这一过程涉及明文的直接传输，攻击者可能通过窃听的方式获得明文和密文，这一过程的安全问题将在5.2 节中进行详细分析。

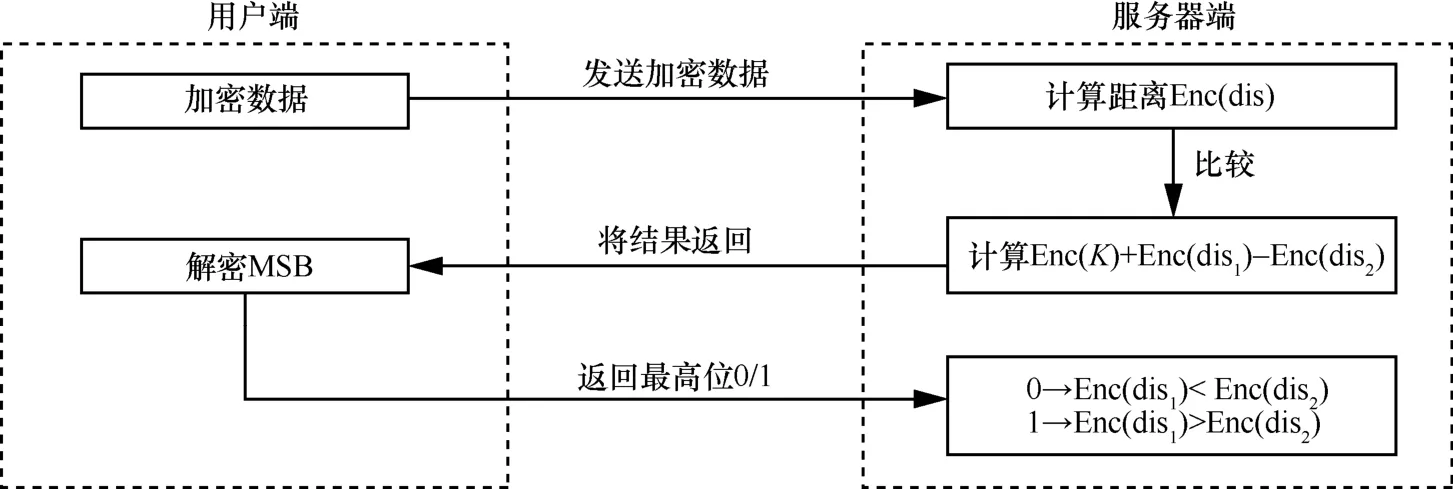
图6 用户端与服务器端的交互场景

4 方案实现

本文实验使用的配置为 Intel(R)Core(TM)i7-6700 CPU @ 3.40 GHz 3.41 GHz，16 GB 内存，借助Helib 同态加密库完成对数据集的加密和同态聚类运算。方案选取2 个常见的聚类数据集。数据集A 是常见形状数据集，共有5 个聚类簇，2 000 条数据，每条数据含有2 个坐标，每个坐标小数点后有10 位小数。数据集B 为Aggregation 数据集，是常用特殊形状聚类数据集，共有750 条数据，每条数据含有2 个坐标，每个坐标小数点后有2 位小数，与整数部分位数基本相同。

本文通过比较明文数据的聚类结果和密文数据上的同态聚类结果来验证方案的准确性。实验中，明文数据集和密文数据集在执行DBSCAN 算法时，所用参数ε和MinPts 一致，实验中ε记作eps，MinPts 记作min_Pts。

4.1 数据预处理方式选取

数据集A和数据集B选取的是常见的聚类算法数据集，分别代表整数与小数部分位数相差较大和较小2 种情况，以此说明本文方案具有普适性。本节通过实验结果来验证3.1 节选取方法的正确性，并得出更适合于数据集A 和数据集B 的预处理方式。实验使用3 种预处理方式分别对2 个数据集编码，然后进行同态聚类操作，得到同态聚类算法的时间开销和同态聚类的准确率，如表1 所示。从表1中可以看出，多元处理编码的准确率是100%，但是时间开销较大；整数对编码和移位舍入编码的准确率虽然均没有达到100%，但也是非常准确的，这说明3.1 节的选取流程中首先将多元处理编码排除，认为数据集A 和数据集B 更适合采用整数对编码方式或移位舍入编码方式，并且对数据集A 中数据的小数部分进行一定程度的舍弃是正确的。此外，整数对编码方式的准确率会略高于移位舍入编码方式，但是移位舍入编码的准确率也非常高，并且移位舍入编码的计算效率远高于整数对编码。实验结果表明，本文实验选取的数据集更适合使用移位舍入编码方式，所以本文实验给出的具体结论都是建立在选择移位舍入编码方式的基础上的。

4.2 数据集明文聚类结果

选取合适的参数，分别对数据集A 和数据集B进行聚类处理，结果如图7 和图8 所示。其中数据集A 选取参数为eps=0.547（编码后为5 470），min_Pts=9；数据集B 选取参数为eps=1.8（编码后为180），min_Pts=11。

4.3 数据集密文聚类结果

对数据集A和数据集B分别进行移位舍入编码处理后再加密，然后对加密后的数据执行同态聚类操作。对数据集A 中的数据进行移位舍入编码处理，结果分别保留3、4、5 位小数，而后在密文上执行同态聚类算法，解密后的聚类结果如图9～图11 所示。对数据集B 直接进行移位舍入编码，加密后进行同态聚类，计算结束后解密得到的聚类结果如图12 所示。

表1 不同编码方式时间开销与准确率

图7 数据集A 明文聚类结果

图8 数据集B 明文聚类结果

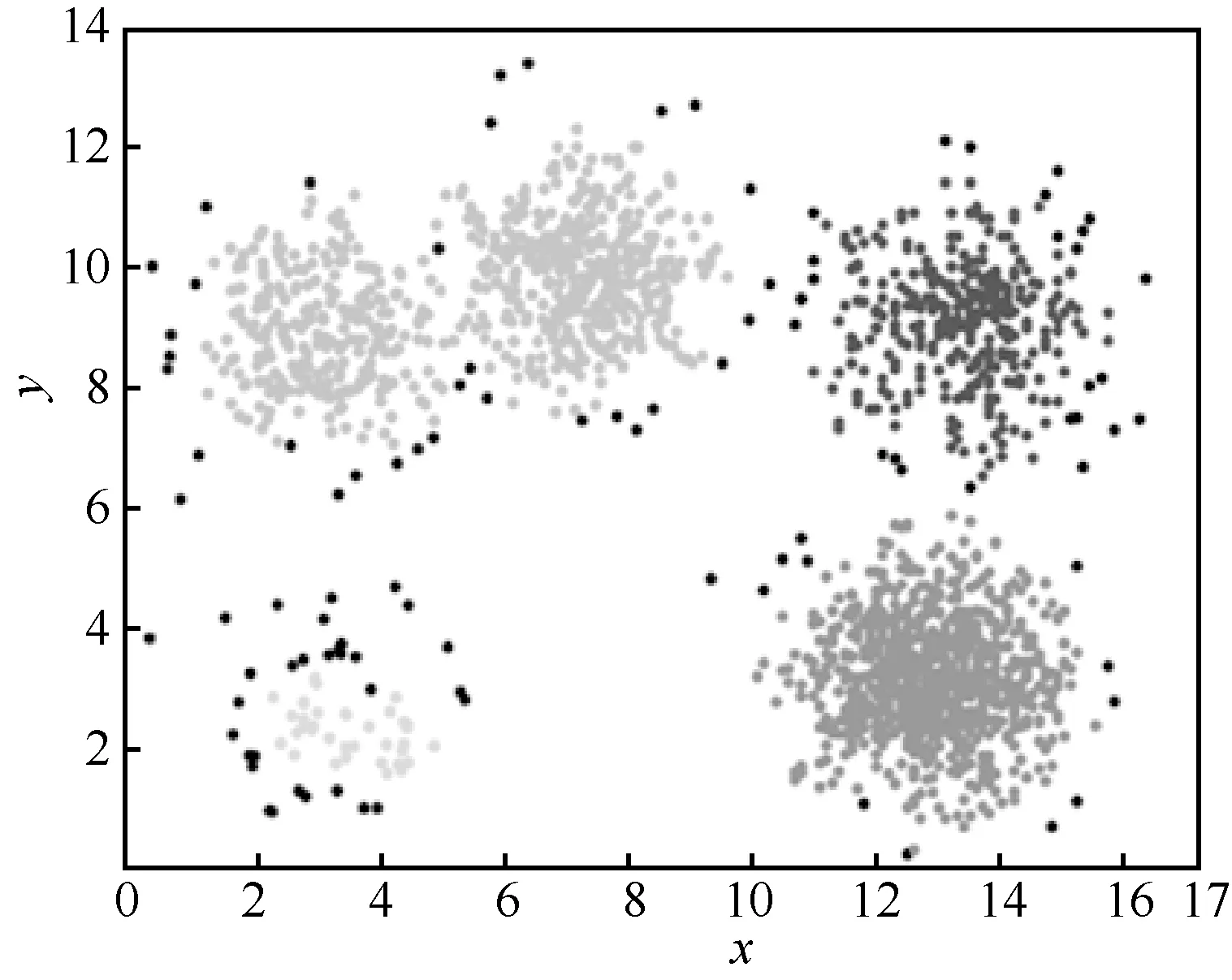
图9 数据集A 保留3 位小数密文聚类结果

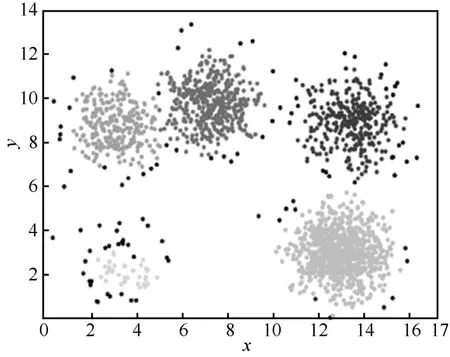
图10 数据集A 保留4 位小数密文聚类结果

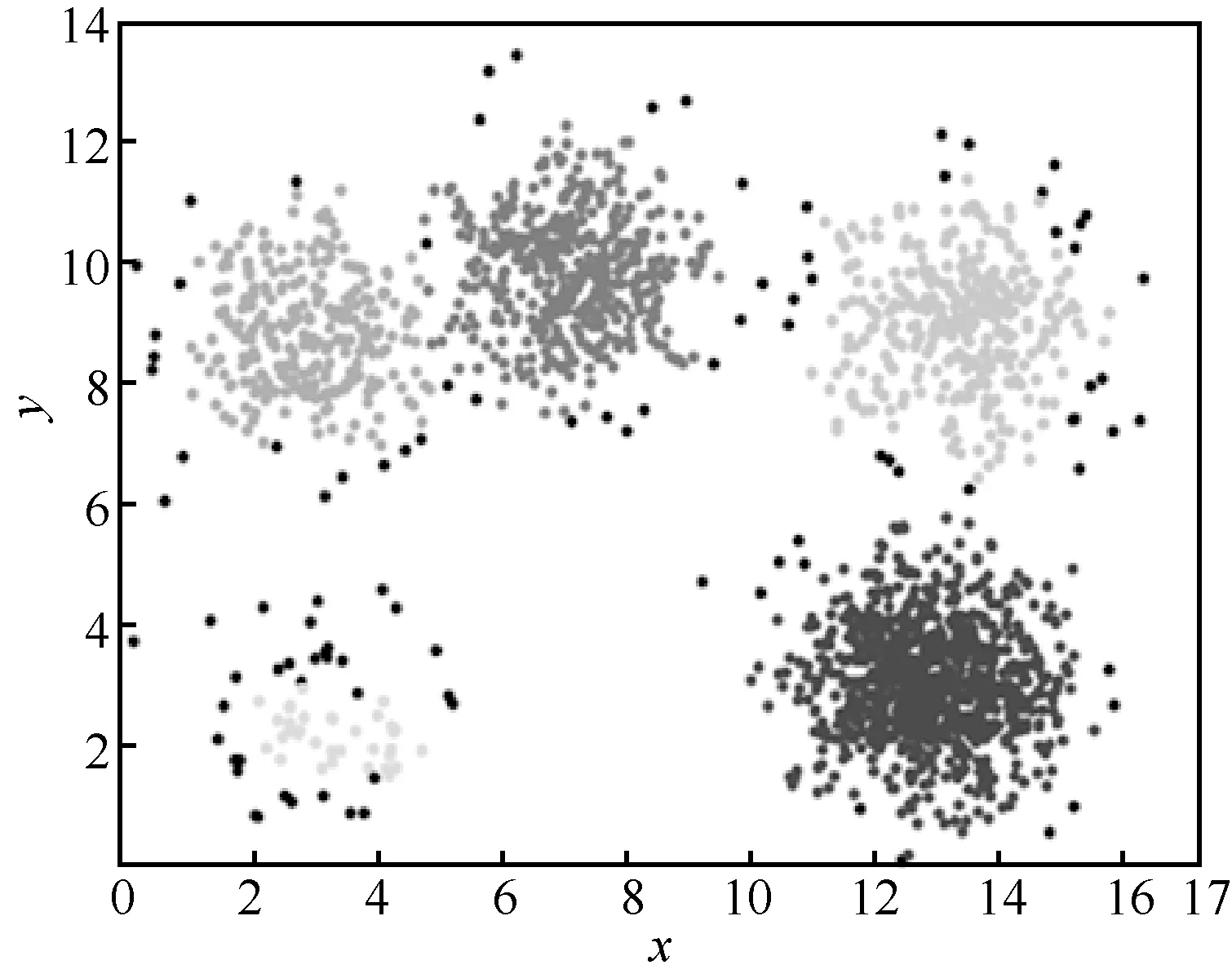
图11 数据集A 保留5 位小数密文聚类结果

图12 数据集B 密文聚类结果

5 方案评估

5.1 实验结果分析

本节分别对比数据集A和数据集B的明文和密文聚类结果，得出方案准确率如表2 和表3 所示。

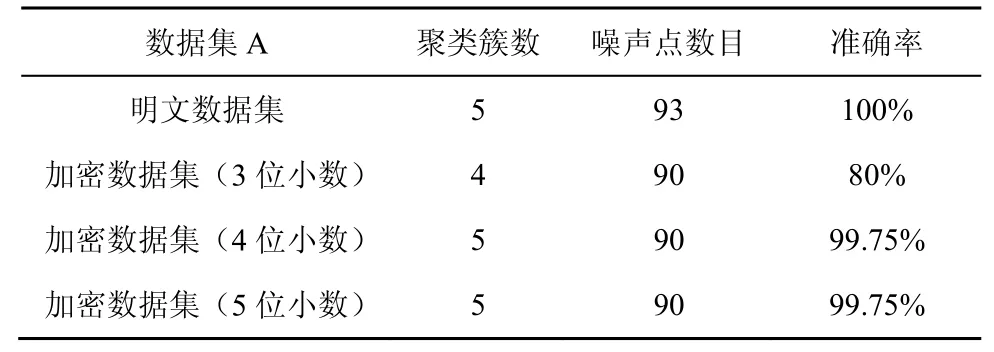
表2 数据集A 明文和密文聚类结果对比

表3 数据集B 明文和密文聚类结果对比

从表2 可以看出，预处理时保留3 位小数的加密数据集的聚类簇数与明文有较大差异，准确率仅为80%；进一步保留精度的加密数据集（4 位小数和5 位小数）具有更好的聚类准确性，这2 种情况下的准确率约为99.8%。表3 结果显示，在数据集B 的聚类结果中，明文和密文聚类簇数相同，噪声点数目接近，准确率在99.7%以上。文献[20]给出了现有其他使用同态加密实现机器学习隐私保护方案的准确率，平均准确率为95%，最高准确率为99.8%，因此相较于此前的方案，本文方案实现了较高的准确率。

时间开销方面，方案[8]对数据进行逐比特加密，导致运算时间较长，对400 条密态二维数据的处理时间长达15 h；本文方案时间开销较低，在处理数据集B 时，对750 条密态二维数据进行同态聚类算法仅需45.28 s。

聚类结果出现误差的主要原因包括2 个方面：一方面是实际数据的舍入误差，考虑到后续加密时间开销问题，在数据预处理阶段对数据的精度进行了一定程度的舍弃；另一方面，由于本文方案中的密文比较协议仅能得出两密文之间的大于或小于关系，对于等于关系直接将其归入大于的范围内，这会造成一定误差。针对第二个问题，可以考虑采用数值比较器进行改善。HElib 已有相关函数，但该函数需要多次密文乘法操作，大大影响计算效率。

5.2 安全性分析

本节将对本文方案的安全性进行评估。在本文方案中，将云服务器设定为诚实但是具有好奇心的半诚实模型，选取的BGV 算法是满足语义安全的同态加密算法。

本文方案希望达到的安全目标为云服务器和具备窃听能力的敌手无法获取用户的数据信息，也无法通过同态DBSCAN 算法倒推出原始数据。在以上设定的前提下，下文将给出几个定理并进行证明，以说明本文方案的安全性。

定理3云服务器或具备窃听能力的敌手根据他们获取的信息成功恢复用户原始数据的概率是可忽略的。

证明云服务器或具备窃听能力的敌手能够获得的数据为和参数〚ε〛、MinPts。从数据的组成来看，除了MinPts 之外，其他都是通过BGV 同态加密得到的密文。云服务器和敌手在不知道私钥的情况下成功获得用户原数据的概率等同于攻破BGV 算法的概率。由同态加密算法的语义安全可知，攻破BGV 算法的概率是可忽略的，因此云服务器和敌手成功获取用户数据的概率也是可忽略的。云服务器或敌手能够获得的数据中唯一的明文是MinPts，而此明文只是表示聚类簇中包含的最小数据个数，并不会泄露用户的任何数据。

此外，本文方案中涉及云服务器与用户之间的一个协议。本质上来说，在此协议中云服务器将一个BGV 密文发送给用户，用户返还给云服务器0或1。云服务器或敌手在不知道私钥的情况下，无法获得该密文的具体内容，并且此时的用户返还的明文（0 或1）和其对应的云服务器发送的密文也不构成密码学中定义的“明密文对”，因而无法在获取足够多的0 或1 明文与其对应密文的情况下推测出密钥。证毕。

定理4云服务器或具备窃听能力的敌手获取同态DBSCAN 算法后，能够成功获得用户原始数据的概率是可忽略的。

证明云服务器或具备窃听能力的敌手可能通过窃听等手段获得在云端执行的同态DBSCAN算法的具体内容。DBSCAN 是一种无监督型机器学习算法，即不需要通过设立训练集预先构建出模型再利用该模型对其他数据进行处理，而是直接在数据上进行聚类操作得到结果。本文方案保留了DBSCAN 算法的这一特点，直接作用于密文数据来获得同态聚类结果，并不存在模型。与分类器的隐私保护方案不同，利用模型参数倒推用户原始数据这类攻击无法应用于本文方案。另外，本文方案实质上进行的运算是依据密文数据同态计算距离，然后给每个数据点标记其归属的聚类簇或将其标记为噪声点，因而攻击者即使获取了算法过程，也无法通过算法内容来推测出原始数据信息。因此，本文方案的数据安全性立足于加密算法的安全性。

综上，攻击者获得同态DBSCAN 算法后，能够成功获取用户原始数据的概率等同于攻破BGV 算法的概率，由定理4 可知，此概率是可忽略的。证毕。

6 结束语

本文提出了一种在加密数据集上进行同态DBSCAN 聚类算法的方案，用于解决数据外包计算过程中的隐私保护问题。该方案针对不同数据集精度，提出了多种编码预处理方式，并且给出了一种基于数据集特点、综合考虑数据精度和计算开销等方面的数据预处理方式的选取策略；依据同态加密算法支持的运算类型和实验测试结果，选取变形欧氏距离作为算法中的距离测度；针对同态加密算法

不支持的比较运算，设计了一个交互协议来实现此功能。本文方案具有可靠的数据安全性、良好的聚类效果和计算性能。