基于分时MDP 的出租车载客预测推荐技术研究

王桐，高山，龚慧雯，孙博

（1.哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001；2.哈尔滨工程大学先进船舶通信与信息技术重点实验室，黑龙江 哈尔滨 150001）

1 引言

出租车空载时间是影响运营收益的主要因素之一。据调查，一些大型城市的出租车空载率已经高达40%～50%[1]，造成这一现象的主要原因是出租车在寻客时具有随机性，司机对寻客路线和寻客地点缺乏足够的认知。虽然打车软件使出租车司机有了明确的载客地点，但仍属于被动寻客模式，即在收到乘客的需求订单后才能出发，当没有乘客需求时，出租车又会处于盲目寻客状态。针对上述问题，需要从全局优化角度出发，为出租车提供明确的主动寻客策略。

出租车轨迹数据挖掘是智能交通领域研究的主要方向之一[2-3]。传统的方法[4-6]利用模糊聚类定义隶属度值，模糊地将对象划分为多个簇，无法保证在复杂城市环境中实现高准确度的预测和推荐。结合历史轨迹进行数据分析并用于优化出租车系统已经得到了广泛的研究[7-8]。目前，对该问题的多数研究根据热点信息及热点间距离进行推荐[9-13]，而没有考虑空载时间，不能更好地反映出租车载客情况。由于出租车之间存在竞争性，即使热点乘客数量多，也未必容易载客，即缺少对热点载客概率等影响因素的充分考虑[14-15]，载客热点间转移概率的研究缺乏实时性。因此，构建更合理的“智能”出租车推荐策略是十分必要的。

本文以北京市出租车载客为例，对出租车空载时主动寻客、载客系统乘客预测及出租车载客策略推荐展开研究，主要贡献如下。

1)载客热点区域聚类研究中，考虑实际出租车载客点的分布特征，结合K-means 与DBSCAN（density-based spatial clustering of applications with noise）提出KAD（K-means and DBSCAN）聚类方法，使载客点聚类更合理。

2)在乘客预测方面，提出基于循环神经网络（RNN,recurrent neural network）的分段预测（SPBR,segment prediction based on RNN）算法，通过实验与支持向量回归（SVR,support vector regression）、CART（classification and regression tree）和BP 神经网络（BPNN,back propagation neural network）等算法进行对比，以证明SPBR 算法预测的准确性以及多次分段预测的合理性。

3)提出了基于分时马尔可夫决策过程（TMDP,time-varying Markov decision process）的载客推荐策略，引入回报函数来衡量出租车收益，通过仿真验证一个时段内TMDP 策略下出租车期望回报与历史期望相比的优势。

2 相关工作

出租车载客研究主要包括对出租车的路径选择、载客效益、载客推荐实时性等方面。

出租车路径选择方面[16-17]的研究内容主要为向空载出租车司机推荐一条最短时间或最大概率载客的路线。路径研究中主要依据司机的驾驶偏好、指定出发点、目的地和出发时间，从大量轨迹数据中实现个性化的路线推荐[18]。Ge 等[19]提出了一种LCP（longest common prefix）算法，开发了一种高效移动推荐系统，该系统能够为司机推荐一系列可能的乘客潜在点，系统从GPS 轨迹中提取出租车位置痕迹，并将这些位置聚集成多个有代表性的小区域，这些小区域被称为从高利润出租车司机的轨迹中学习的提升点，但这种算法为司机推荐驾驶方向而不推荐具体路线。针对寻客途中出现的道路拥堵现象，主要有2 种不同类型的查询最短路径的算法[20]：Query_FiST 基于堆的Bellman-Ford 算法和Query_BeST 扩展的Bellman-Ford 算法。这2 种算法只考虑了实时交通信息，没有考虑乘客对出租车的需求量。Rong 等[21]考虑目的地对出租车的影响，使用马尔可夫链为寻客过程建模，找到空载出租车的最佳行程，但是热点之间的不确定因素会导致推荐结果的不准确。

在出租车载客效益方面，相关研究[22-23]主要侧重于出租车运营收益，这主要与乘客供求关系、交通状况等信息有关。此外，一些研究从出租车历史收益角度出发，在大规模历史出租车轨迹中挖掘高效运营出租车所行驶的路线，从而提高整体利润[24]。文献[25-26]根据经验丰富的司机产生的历史出租车轨迹，设计了一种两阶段路由算法，为最终用户计算实际速度最快的定制路由，建立智能驾驶方向系统。Yuan 等[27]从乘客角度考虑，基于出租车产生的大量GPS 轨迹检测停车位的方法，设计了一个概率模型来描述与时间相关的出租车行为（上下车、巡航、停车），并为出租车司机和乘客提供全市范围的推荐系统，使其尽可能迅速地载客，并最大化下一次行程的利润。但由于乘客的随机性、流动性过强，在实践中效果不佳[28]。上述方法多数只考虑短期收益，而未考虑未来时间连续载客规划。

载客推荐实时性是研究出租车系统的又一个重要条件，路径动态更新可以保证推荐策略的有效性[26]。Qian 等[29]利用在线地图实时查询方法，定义了3 种路线评价原则，分别为priority principle、decaying principle、sharing principle，进而设计了一个符合出租车司机需求的评价函数，提出了一种路径分配机制来保证出租车司机推荐的公平性，并根据用户需求和实时交通状况给出最佳路径。Huang 等[30]制定了一种TDVRP-PF（time-dependent vehicle routing problem with path flexibility）模型，采用Route-Path近似方法在随机交通条件下为TDVRP-PF 生成近似最优解，将道路网络中的路径选择和时间选择因素相结合，确保了推荐的实时性。Lei 等[31]提出了“虚拟车辆”的概念，通过实时客流分布为出租车提供寻客时间短并且载客概率高的出行方案。“虚拟车辆”之间可以相互通信，了解周围司机的驾驶行为，根据动态交通信息做出决策，从而达到整体车辆的最佳通行效率，但由于使用导航软件的司机都存在自私行为，因此可能导致更严重的交通拥堵。胡昊然[32]提出了一种称为cabrec 的路线推荐系统，提取载客热点，利用启发式算法构造热点树，热点树以当前位置为根节点，连接所有的载客点；同时，提出了一种估计各路线权重的概率模型，并给出了一组加权循环推荐方法。但是，其仅考虑了热点和寻客时间的影响，忽略了热点间的关系，缺乏整体性。

针对上述问题，本文采用回报函数衡量热点区域价值。

3 基于RNN 的载客热点分段预测和TMDP寻客策略推荐

由于乘客具有流动性和随机性[28]，常用算法（如支持向量机、决策树等）很难挖掘乘客数据的内在联系，因此降低了预测的准确性。针对这一问题，本文提出SPBR 算法对出租车行驶区域进行乘客热点分布预测，为出租车推荐寻客策略，实现出租车载客路线的长距离规划。

为更加准确地预测以及合理地推荐，本文设计了出租车载客预测和推荐框架，如图1 所示。该框架分为线下处理过程和线上处理过程两部分，具体流程如下。

1)清洗出租车历史轨迹原始数据，删除无效、重复信息。

2)采用聚类算法处理出租车GPS 信息中的载客点（即乘客上车点）信息，得到载客热点区域。

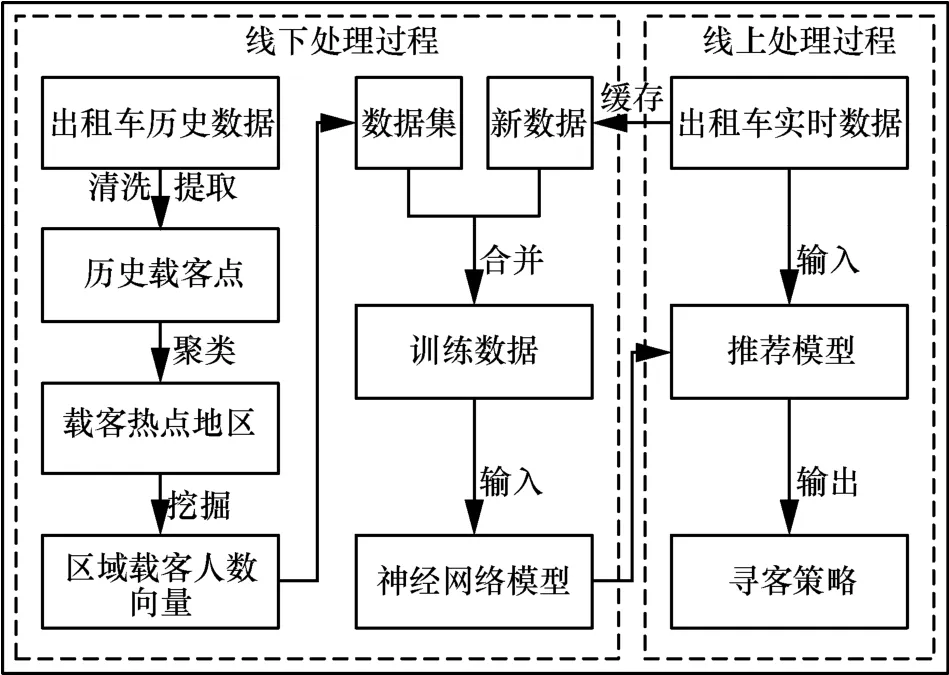
图1 出租车载客预测和推荐框架

3)根据轨迹中的时间戳信息，统计每个区域各时间段的载客人数，得到区域载客人数向量，进而建立载客人数预测模型。

4)获取载客区域最新的载客信息，输入训练好的预测模型中，模型的输出即为预测的乘客数量。

5)将预测结果输入推荐模型，推荐模型结合热点间相关信息实现寻客推荐。

3.1 线下处理过程

由图1 可知，本文算法在对出租车乘客预测和推荐时，需先对数据进行线下处理，包括数据预处理、必要信息的提取以及预测模型的训练。

3.1.1 数据预处理和载客人数向量挖掘

由于出租车原始历史数据中存在大量冗余及无效的信息，需要对其进行清洗以减少存储空间、加快运算速度。本文所用数据来源为北京市28 000 辆出租车在2015 年12 月产生的GPS 轨迹数据，局部清洗后的数据格式如表1 所示。最终提取的载客轨迹为323 752 条，在此基础上分析出租车载客点轨迹的分布情况[33]，选择合适的聚类算法。本文采用KAD 的方式对北京市出租车不同场景下的载客点聚类。

K-means 聚类时，按照载客点之间的距离来区分不同的簇。K-means 算法收敛速度快、易实现，当不同热点区域之间有较明显的区别时，K-means 算法有很好的聚类效果。通过K-means 聚类流程可以发现，算法需要的参数仅目标热点数K，不受其他参数影响。但K值的确定往往比较困难，需要提前对样本集分析来选取较好的K值。根据K-means 算法流程可知，质心的迭代更新是在初始随机选择质心的基础上进行的，这就导致最终聚类结果会受初始质心的影响，所以聚类结果具有一定的不确定性。另外，K-means 算法默认将所有载客点都视为样本，导致其对噪声和异常点比较敏感，如果样本中离散和随机的载客点比较多，会对结果会产生较大的负面影响。

表1 局部清洗后的数据格式

K-means 算法和DBSCAN 算法对郊区载客点的聚类效果如图2 所示。K-means 算法虽然将不同的热点区域明显地进行区分，但由于郊区载客点的稀疏性，一些随机的载客点被划分到不同热点中，导致载客热点区域范围变大，但这些载客点本身不具有可分析性，会导致出租车在某个区域寻客困难而失去推荐的作用。DBSCAN 算法将某些离散点排除，只将密集的载客点聚为一类，每个区域范围较小，提高了对区域进一步处理的准确度，因此，郊区载客点聚类适合采用DBSCAN 算法。

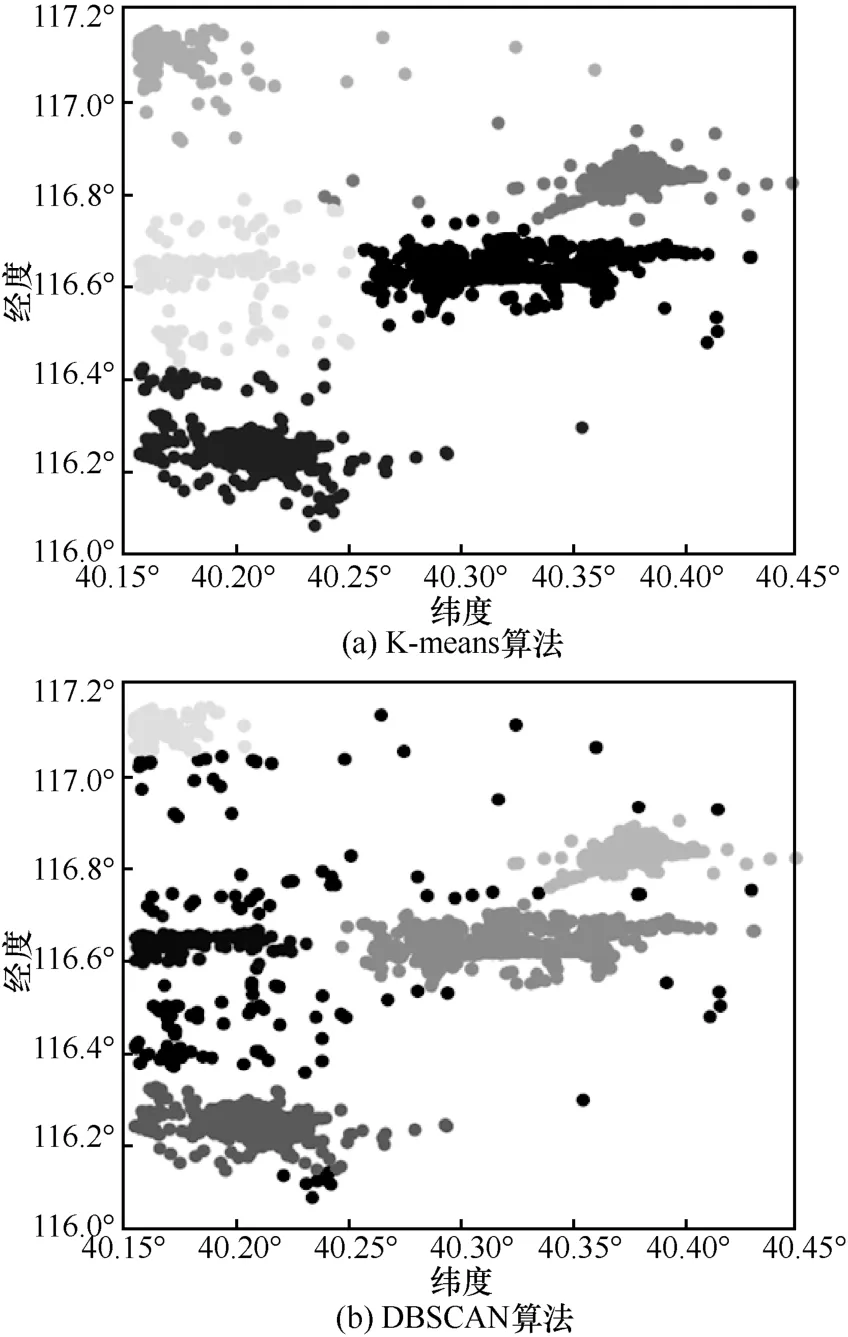
图2 K-means 算法和DBSCAN 算法对郊区载客点的聚类效果

K-means 算法和DBSCAN 算法对市区载客点的聚类效果如图3 所示。从图3 可以看出，在市区中，载客点沿道路呈网络状分布，由于DBSCAN 算法按照密度可以将簇聚类为任意形状，因此DBSCAN 算法最终形成的簇集沿道路分布而不是形成区域，而且由于道路的相互交叉，簇集之间也会以不规则的形状相互交错，这种形式的簇集不适合作为载客热点区域。K-means 算法避免了上述问题，其把载客点划分成相对均匀的若干个载客热点区域，区域间相邻但不发生交错，能够很好地对载客区域进一步处理。

图3 K-means 算法和DBSCAN 算法对市区载客点的聚类效果

DBSCAN 算法的载客热点之间往往相隔一定的距离，这将导致在进行出租车载客推荐时不仅需要载客热点的相关信息，还要考虑从某个热点到另一热点所经路径的有关信息（如路径上的载客概率），这会大大增加数据处理的难度。因此，市区内载客点聚类适合采用K-means 算法。

本文采用KAD 方式对北京市出租车不同场景下载客点进行聚类。已知北京市总面积s=16 410 km2，根据相关文献，出租车平均寻客时间z=15 min[34]，假设出租车行驶的平均行驶速度为v=30 km/h[35]，则划分的区域半径r=vz/60，则载客区域个数n=s/r2=93，为便于分析和计算，本文将载客区域数量设为n=100。郊区采用DBSCAN 算法，调整参数进行仿真，直到每一簇都具有较好的聚类效果，此时聚类结果为32 个热点区域；基于K-means 算法的市区载客点聚类设定热点数量为K=68。依次标记郊区热点区域为0～31，市区热点区域为32～99。

为保证时间有效性，出租车载客区域还需与每个区域不同时间段历史载客人数相对应。根据平均寻客时间，令每段时间z=15 min，即将每个区域全天划分成24×60/15=96 个时间段。根据GPS 轨迹所包含的时间戳，统计各个时间段内载客点的数量，对每个区域进行向量化处理构成96 维的向量。以区域i为例，每天载客人数向量为Vi={b0,b1,…,b95}，扩展到一个月（即30 天），则Vs={b0,b1,…,b2879}，得到区域i的载客人数向量数据集为

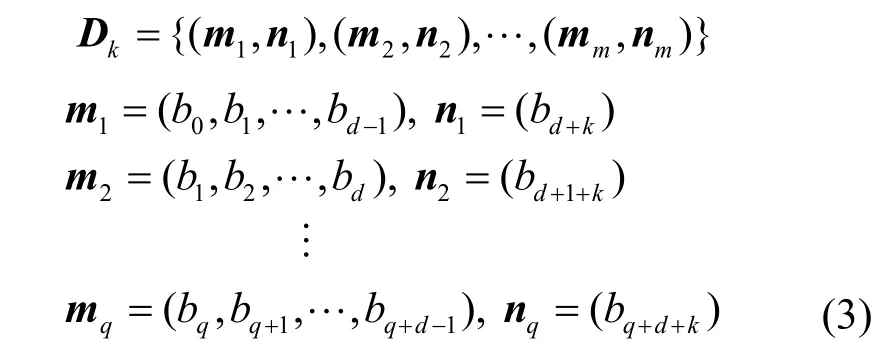
其中，m表示预测模型的输入；n表示输出对比；d表示用于预测的时间长度；k表示当前时间段与预测时间段的间隔数，例如，k=0 表示通过前d段数据预测第d+1 段的载客人数，k=1 表示通过前d段数据预测第d+2 段的载客人数，即输入和输出时间段距离为2。

3.1.2 神经网络预测模型

对于出租车载客热点预测问题，由于大数据的复杂性，用传统机器学习算法进行预测会达到极限，而神经网络在海量数据面前能够展示自己的潜力。另一方面，在出租车乘客预测中，载客人数具有时序性，经典BPNN 难以表征时间序列数据的内在联系，神经网络中隐藏层的值只取决于当前输入，不同样本间的输入、输出相互独立，许多情况下不能实现很好的预测，因此本文结合RNN 的思想，对出租车乘客数量进行预测。

本文出租车乘客数量的预测中，采用RNN 作为预测模型，模型输入为历史前d段载客人数，输出为第d+1 段的载客人数，即循环神经网络输入层为d维向量，输出层为一维向量。考虑出租车载客系统长期的优化，仅得到未来最近一段时间的预测结果是不够的，因此，本文进一步地提出SPBR 算法对出租车系统进行未来多个时间段的人数预测。

各个区域乘客信息通过式(3)提取处理得到数据集Dk，k=0,1,2,…。将数据集Dk的70%作为训练集输入RNN，剩余的30%作为测试集。在实际训练中对隐藏层层数、每层神经元个数以及神经元激活函数等参数不断优化，训练得到与k有关的K_RNN 模型。预测出租车乘客数量时，从当前每个区域数据中获取最新d段载客人数，根据预测目标段加载对应K_RNN 模型，模型的输出即为相应时间段的预测值，最后将所有预测值生成向量作为推荐的基础。SPBR 算法预测模型结构如图4 所示。

图4 SPBR 算法预测模型结构

根据k的不同取值，SPBR 算法能够有效地挖掘某一时间段输入与输出值的内在联系。通过多次分段预测准确获取热点区域未来每个时间段的载客人数，并将预测结果生成向量用于推荐。同时，对训练集进行更新，采集区域产生的实际载客信息进行缓存，当缓存数据达到一定量时，将其加入训练集并重新训练K_RNN。随着训练数据的不断积累，得到的乘客预测模型将具有更强的拟合能力，进而保证了数据集的有效性以及预测结果的准确性。

3.2 线上处理过程

由图1 可知，通过线下处理，乘客数量预测可以为出租车司机提供更准确的载客参考，但考虑到载客区域之间的联系以及出租车长期的收益，单纯将所有区域的乘客预测信息推荐给司机缺乏实际依托。因此，本文拟建立一个出租车载客推荐模型，对实时数据进行线上处理。当出租车处于空载时，依据所在区域及其他各区域的相关信息（包括载客、转移概率等信息），结合SPBR 算法预测的各区域未来可能的乘客数量，共同输入推荐模型，以计算出更优的载客策略进行推荐。

3.2.1 基于MDP 的载客推荐模型

出租车载客推荐框架的难点在于如何构建合理的推荐模型。该模型需考虑出租车载客推荐的特点，模型输出的载客策略相当于司机所采取的行为，并且最终载客结果只由当前所在区域及采取的行为决定。该推荐模型具有随机性策略与回报，为序贯决策的数学模型，因此本文采用马尔可夫决策过程（MDP,Markov decision process）为出租车司机提供合理的载客策略。

将MDP 表示为一个五元组(S,A,Psia,γ,Rsia)。MDP 方法与出租车载客推荐问题相结合，则司机在载客点的行为集合A={等待,移动到其他区域}，而出租车司机对下一载客点的选择取决于当前所在位置，符合MDP 无后效性的性质；Psia为载客区域si∈S下司机进行动作a∈A后转移到下一载客区域的概率矩阵；γ∈(0,1)为折扣因子；Rsia是在状态si∈S下进行a∈A后的回报；S在MDP 中表示可能的状态集合，此处结合出租车推荐问题表示载客区域集合，数量N=100。

3.2.2 分时马尔可夫决策过程

MDP 中状态转移概率矩阵Psia是固定不变的，即载客区域之间的转移概率固定。该假设显然不符合出租车载客的实际情况，区域之间的转移概率在一天之中会随着时间的变化而改变。例如，早上的乘客偏向从生活区到工作区，而傍晚的乘客更偏向由工作区返回生活区。因此，通过传统MDP 寻找最优载客策略缺乏合理性。为满足区域之间的转移概率随时间段变化的特点，本文提出TMDP 用于推荐司机寻找最优载客策略。

TMDP 中的转移概率矩阵Psia如表2 所示。将15 min 划分为一个时间段，TMDP 将每个载客区域扩展为96 个时段。(0≤i≤99，0≤m≤95)表示区域i的第m个时间段的状态，因此状态集合S的数量扩展为N=100×96，行为a下的TMDP 转移概率矩阵为9 600×9 600 的矩阵。

表2 TMDP 中的转移概率矩阵Psia

TMDP 中将状态集合由单纯区域集合扩展为区域加时间段集合，状态转移概率矩阵Psia的复杂度随之提高。当行为是等待时，区域不会发生变化，且出租车不可能由未来回到过去，所以在a为等待的情况下，只有当i=j且n不是m之前的时段时有意义，其余为0；在a为移动到其他区域的情况下，只有当i≠j且n不是m之前的时段时有意义，其余为0。

当时间段m=95 时，未来时段从第二天的m=0时段算起，因此，表2 是可循环的。例如可以表示在区域0 从第一天的第95 个时间段到区域0第二天的第0 个时间段的转移概率，可以表示在区域0 从第一天的第95 个时间段到区域1 第二天的第0 个时间段的转移概率。由于分时马尔可夫决策过程和马尔可夫决策过程一样为无限步骤，即

因此，表2 的可循环性能够很好地满足分时马尔可夫决策过程。在出租车系统中，出租车的收益受到各种因素干扰，所以回报函数应考虑多方面的影响。出租车的空载对其收入回报呈负面影响，而载客区域的预期载客人数及载客概率对收入呈正面影响。定义从状态到的回报为

其中，表示在时段n中所有经过区域sj时发生空载状态的出租车数量，即在区域sj的时段n内，出现过载客状态为0的出租车数量；表示时段n内在区域sj寻到客的出租车数量，即在区域sj的时段n中，载客状态由0 跳变为10 000 000 的出租车数量。

由式(5)可知，出租车的载客回报与下一载客区域的预测载客人数以及载客概率成正比，与从当前区域到下一区域的空载寻客时间成反比，考虑所有区域和所有时间段，通过式(5)得到的回报函数可以表示为矩阵R∈9600×9600。参照3.1.2 节，由于预测得到的未来多个时间段的载客人数因输出段与输入段距离增加导致预测误差扩大，且出租车司机更注重较近时段的收益。因此，在TMDP 中引入折扣因子，累计回报表示为

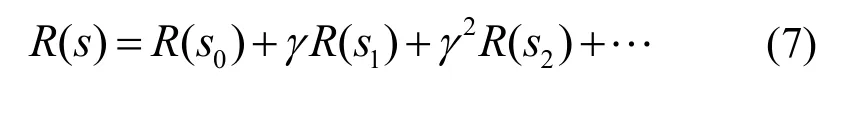
其中，R(s0)表示在当前状态s0采取行为后达到下一状态s1的回报，R(s1)表示在状态s1采取行为后到达下一状态s2的回报，依次类推。状态、行动、转移概率和回报间的关系如表2 和式(5)所示，转移概率以及回报由初始状态和采取的行动决定。TMDP 可以表现出各区域各时间段之间的关系，因此能够得到更加合理的载客策略推荐结果。综上所述，TMDP 推荐模型可以表示为五元组(S∈1×9600,A∈ℜ1×2,P∈ℜ9600×9600×2,γ,R∈ℜ9600×9600×2)，其中，折扣因子γ由具体情况决定。

3.2.3 状态转移概率矩阵的提取

构建TMDP 的模型后，需要获取状态转移概率矩阵P。线下处理清洗数据后，从表1 中可知，在同一出租车ID 下，载客状态由0 到10000000 表示出租车的空载到载客的过程，载客状态由10000000到0 表示出租车从载客到空载的过程。针对出租车载客策略，对表1 数据进一步过滤，使每辆出租车的起始状态都从空载开始，到载客结束。

由于热点的划分按照不同区域由KAD 方法聚类得到，分别用0～99 代表聚类得到的100 个载客区域，计算每条寻客轨迹的所属区域，并将区域标号作为新的字段添加到轨迹信息中。基于TMDP 的推荐是随时间变化的，区域间的转移概率可根据时间步长Ts=15 min 划分的时间段来求得。又因为TMDP 的状态转移概率与行为a有关，求解转移概率矩阵（a为移动）的具体步骤如下。

1)查找出租车在区域s中某一时间段t的轨迹点。遍历数据集D，如果D中某条轨迹所属区域为s，其时间戳对应所属时间段t，且该轨迹为空载状态，将其标记为(s,t)。

2)求(s,t)在a为移动时的转移概率。(s,t)下一条为同一出租车在载客状态下的轨迹信息，判断载客状态的轨迹点所属区域，若不属于s，则说明该出租车在其他区域s'寻到乘客，根据时间戳求得在s'时所属时间段t'。统计从(s,t)出发到所有其他(s',t')载到乘客的轨迹点数量，并计算概率得到执行动作a为移动时(s,t)的转移概率p1(s,t)。具体判断的条件为

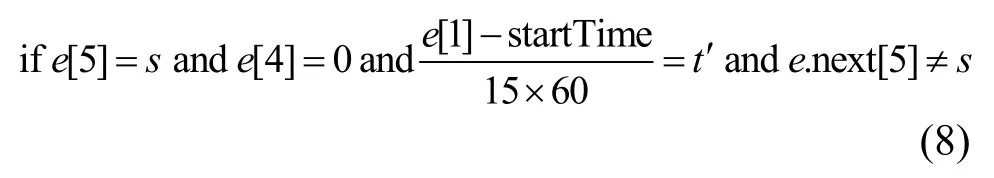
其中，e是数据集D中的一条轨迹，e[0]是出租车编号，e[1]是时间戳，e[0]是纬度，e[3]是经度，e[4]是载客状态，e[5]是轨迹所属区域，e.next 是轨迹e的下一条轨迹，startTime 是一天的初始时间戳。

3)求(s,t)在a为等待时的转移概率。如果(s,t)下一条载客状态的轨迹点仍属于区域s，说明该出租车接到乘客，根据时间戳求得在区域s载到乘客时所属时间段t'。统计从(s,t)出发到所有其他(s,t')载到乘客的轨迹点数量，并计算概率得到执行动作a为等待时(s,t)的转移概率p2(s,t)。判断的具体条件为

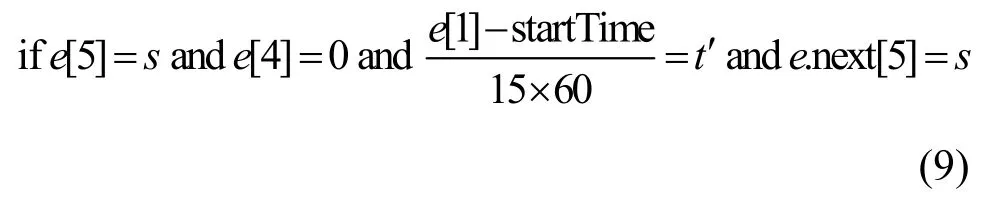
4)求转移概率矩阵。将s扩展成S=[0,100]，t扩展成T=[0,96)，得到a为等待时的概率转移矩阵P1，a为移动时的概率转移矩阵P2。生成和行为有关的状态转移概率矩阵的具体方法为

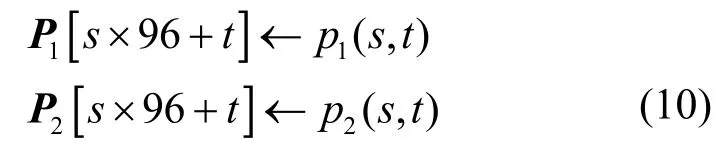
可见P1和P2是不同行为对应的9 600×9 600转移概率矩阵，最终状态转移概率矩阵表示为P=[P1,P2]。

3.2.4 TMDP 回报矩阵分析

由式(5)可知，回报矩阵R需根据载客概率矩阵Q、寻客时间矩阵E及预测的载客人数矩阵X得出。

1)载客概率矩阵Q

每个区域的载客概率由历史轨迹数据统计得到，与当前所执行的行为无关，因此载客概率矩阵不需要划分不同行为。根据式(6)分别求出100 个区域在96 个时间段的载客概率矩阵Q∈ℜ100×96，则回报函数矩阵表示为R∈ℜ9600×9600，为保证数据形式的一致性，需要先将Q∈ℜ100×96转化为Q∈ℜ1×9600，然后对Q∈ℜ1×9600复制9 600 次得到Q∈ℜ9600×9600。

2)寻客时间矩阵E

从状态到的平均寻客时间为

其中，当从状态sim不可能到达sjn时，，从而说明该情况下达到最差回报。为了避免过小引起计算的不方便，引入参数3 600。

3)载客人数矩阵X

Xjn是通过SPBR 预测得到的区域sj在未来第n个时段的乘客人数。TMDP 的状态−值函数为

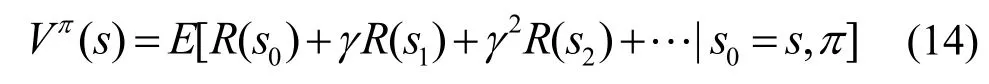
随着SPBR 输入时间段和输出时间段距离的增加，预测未来无限个时间段的载客人数误差会越来越大，考虑到出租车司机对近期收入的注重，因此没有必要预测距离当前过远的时间段。适用于TMDP 的Xjn为

其中，l为确定输入段和输出段的临界距离。当距离小于或等于l时，Xjn由SPBR预测得到；当距离大于l时，Xjn取训练集数据对应时间段的平均值。

3.2.5 TMDP 求解过程

TMDP 的状态−值函数可表示为

TMDP 的目的是求解最大期望回报，即最优状态−值函数V*(s)，从而得到最优策略π*(s)，最终将最优策略推荐给出租车司机。本文采用策略迭代算法求解TMDP，策略迭代算法如算法1 所示。

TMDP 求解过程从初始化策略出发，实施策略评估，改进策略，经过持续迭代更新，直到策略收敛。具体步骤如下。

1)初始化所有状态的V(s)以及π(s)（初始化为随机策略）。

2)用当前的V(s)对策略进行评估，计算出每一个状态的V(s)，直到V(s)收敛。

3)用步骤2)得到的当前策略评估函数V(s)进行改进，在每个状态s时，对每个可能的动作a，计算采取这个动作后到达下一状态的期望，选取期望价值函数最大的动作来更新策略π(s)，然后再次循环步骤2)和步骤3)，直到V(s)和π(s)全部收敛。

策略迭代过程如图5 所示，该过程是一个反复优化状态−值函数V和策略π的过程，当V(s)和π(s)全部收敛时即可得到最优策略π*和最优状态−值函数V*。

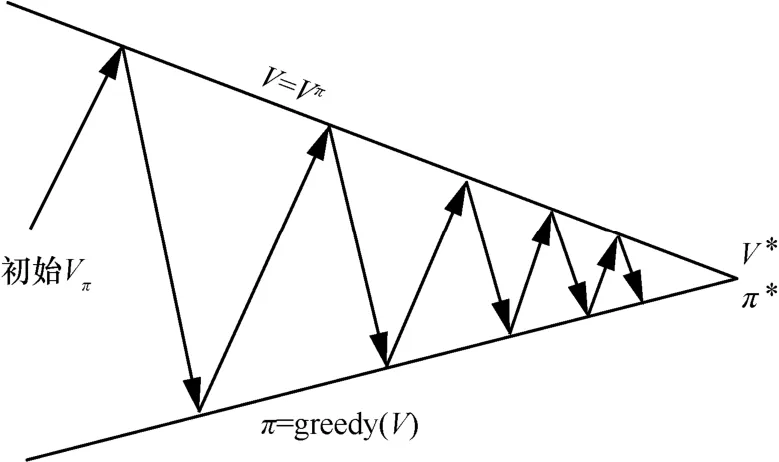
图5 策略迭代过程

通过TMDP 求出最优策略的矩阵形式如表3 所示。表3 为出租车在每个区域每个时间段下应选的最优载客策略，其中，1 代表在当前区域等待，2 代表去其他区域寻客。出租车处于空载状态时，确定所处区域和对应时间段，通过与表3 匹配得到最优策略。当推荐的最优策略为2 时，出租车应在当前区域继续等待。当推荐的最优策略为1 时，出租车应主动到其他区域寻客。

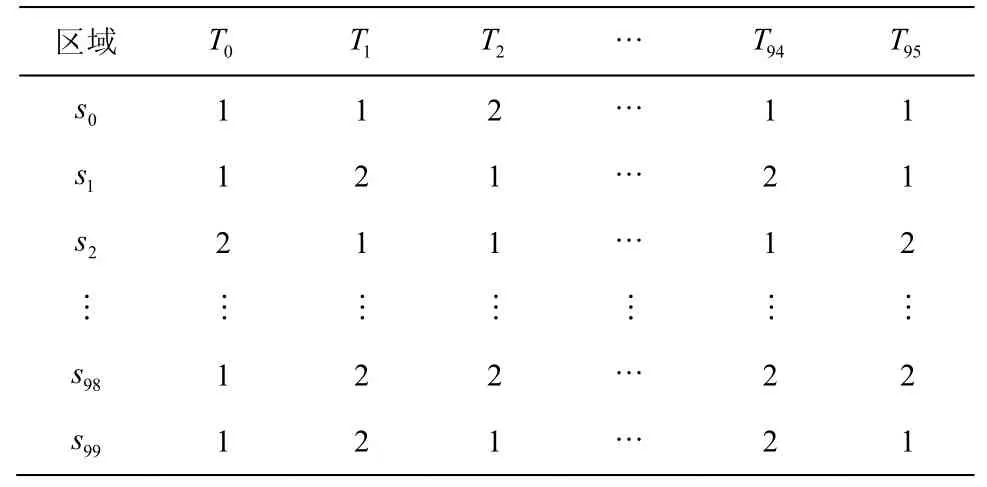
表3 TMDP 最优策略矩阵形式

4 实验结果与分析

4.1 乘客热点区域的预测结果及误差分析

通过对出租车预测模型进行仿真，本文进一步对影响预测结果的因素进行讨论，并将其准确性和实际要求相结合进而确定相关参数，以达到准确度与实用性的统一。

4.1.1 预测结果及性能比较

在预测模型中基于RNN 对出租车历史载客数据进行分段训练和预测，将载客数据集的70%（21天）用于神经网络的训练，剩余30%（9 天）作为测试，设每段时间步长Ts=15 min，用于预测的历史时间长度e=1，令k=0，即SPBR 输入和输出的数据没有时间段间隔。SVR、CART 和BPNN 作为比较算法。利用相同数据集分别训练SVR、CART、BPNN 和SPBR 模型并进行预测，结果如图6 所示。

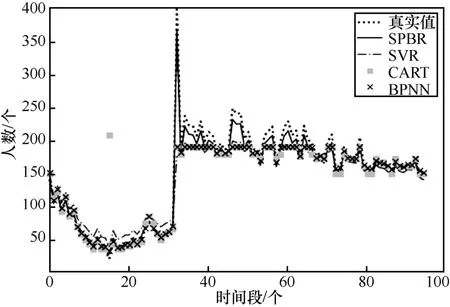
图6 预测结果对比

从图6 可以看出，SPBR 整体预测性能较好，能够准确还原每一时间段的乘客数量变化趋势。为进一步评估算法预测效果，采用均方根误差（RMSE,root mean square error）和平均相对误差（MRE,mean relative error）衡量预测算法性能。

其中，pre 为算法预测结果序列，true 为实际序列，m为序列长度。SVR、CART、BPNN 和SPBR 预测结果误差对比如图7 所示，相较于SVR、CART、BPNN，SPBR 的RMSE 分别降低了67.6%、71.1%、64.5%，MRE 分别降低了59.1%、58.3%、6.0%。

图7 算法误差对比

结合图6 和图7，在00:00～06:00（即时间段0～24），乘客稀疏并且偶然性较大，在SVR 中很难找到完全契合本数据集的核函数，导致SVR 的预测结果出现一定程度的偏离；基于CART 的预测结果在该时间段有着较高的拟合程度，但由于异常突发值的存在导致误差扩大；BPNN 和SPBR 在该时段可以很好地拟合。

6:00 之后的时间段，SVR、CART 和BPNN 的预测结果比真实数据的波动平缓，但只能在大致趋势上还原，尚缺乏局部准确性。SPBR 由于其强大的自组织能力以及针对时间序列的递归性，可以捕捉到前后数据间的关系，对全天数据可以很好地拟合。

4.1.2 历史时间长度对预测结果的影响

本节对e的最佳取值进一步讨论。历史数据中，各时间段的载客人数有潜在的联系，因此历史时间长度的选取对预测结果有着不可忽略的影响。

历史时间长度e决定RNN 输入层的纬度，即输入层神经元的个数，所以选取不同的e，RNN 的结构会发生改变并需要重新训练。令e=1,2,3,4,5,6。设k=0，处理数据得到数据集Dke。Dke的70%用于训练RNN，30%用于测试，图8 为测试集不同e下的平均误差比较。根据图8，对于SVR 和CART，当e=2 时误差达到最小，但误差仍大于RNN；SVR和BPNN 的RMSE 随e的变化不明显，但MRE出现较大起伏。因此，结合RMSE 和MRE 衡量各算法的预测误差是合理的。当e=1 时SPBR 误差最小，因此用SPBR 进行载客数量预测时只需要根据前一段历史数据即可保证对下一段预测的最小误差。

图8 测试集不同e 下的平均误差比较

4.1.3 分段预测

基于RNN 的多次分段预测方法中，输出层神经元数量为1，每次预测只得到未来某一个时间段的载客人数。SPBR 通过多次预测可得到未来每个时间段的预测数据，进而得到多段预测结果。使用回归预测时，神经网络本身可以通过增加输出层神经元数量实现对未来的一次性多段预测，例如预测某个区域未来6 个时间段的载客人数，只需将RNN 输出层神经元数目设定为6 就能一次性完成预测。

将Dk的70%作为训练集，30%作为测试集，令k=0,1,2，e=1，即利用某个区域历史时间段的载客人数分别预测未来最近3 个时间段的载客人数，RNN 输入和输出层神经元个数都为1，分别训练得到与k有关的K_RNN 模型，9 天数据的平均预测结果作为测试集，对应误差如图9 所示。随着RNN输入时间段和输出时间段距离的增加，SPBR 模型预测误差变大。

图9 分段预测结果对应误差

作为对比算法，多段预测的数据集设置方式选用与分段预测相同，令历史长度e=1，k=2，即一次性预测时间段数为3，得到的每个时间段平均预测结果及误差如图10 所示。

对比图9 与图10 的预测结果可知，多段预测能一次性得到未来多段的结果，且3 个时间段的预测误差很接近。但由于训练时要兼顾多段预测的准确度，导致不能充分学习每段输出与输入之间的关系，因此预测误差整体偏大。SPBR 通过单独训练每段数据能够最大限度地拟合。同时在实际情况中司机更注重的是近期收入，因此要保证第一段预测的准确性，SPBR 对每个时间段分别预测满足了这一要求。通过比较发现，即使输入段与输出段的距离增大后SPBR 预测结果的误差也随之增大，但相同时间间隔下仍比一次性多段预测更准确。

4.1.4 时间步长对预测结果的影响

前文分析中，时间划分默认为15 min/段，但实际中选取时间步长对预测结果的影响需要进一步讨论。令时间步长Ts分别为10 min/段、15 min/段、20 min/段、30 min/段，用于预测的历史时间长度e=1，预测目标是下一段的载客人数。

图10 多段预测结果及误差

基于SPBR 的不同时间步长的预测结果及误差如图 11 所示。当时间步长Ts=10 min 时，RMSE=9.46，达到最小，但此时MRE=0.133，远远大于其他情况。这是因为当Ts较小时，每段步长所对应的累计载客人数同样较少，导致即使预测偏差较大也会因为基数小而使RMSE 较小。综合RMSE和MRE 可知，步长Ts=15 min 最合适。

4.1.5 过拟合对预测结果的影响

由于训练数据包含抽样误差，在训练时神经网络将训练集中独有的特征视为整个数据集的共有特征，由此产生的过拟合是神经网络中的常见问题，即在训练时误差不断下降但测试集误差却上升。为避免过拟合，在网络中添加了Dropout 层，其原理是模型每次更新参数时随机断开一定百分比的输入神经元连接。

图11 基于SPBR 的不同时间步长的预测结果及误差

经过多次调参和训练发现，更新参数时随机断开20%的输入神经元连接可以实现有效改进。如图12 所示，添加Dropout 层的RNN 的拟合效果明显优于未添加Dropout 层的RNN。

4.2 载客推荐结果分析

本文采用TMDP 算法实现基于SPBR 预测结果的出租车司机载客策略推荐。假设当前时刻为t0，历史长度e=1，时间步长为15 min/段，因此获取t0时刻前15 min 各载客区域的上车人数作为SPBR 预测模型的输入，预测结果中未来多段的乘客人数作为TMDP 的推荐基础。

图12 Dropout 层对预测误差的影响

4.2.1 TDMP 回报矩阵分析

本节实验分析TMDP 回报矩阵中载客人数矩阵的X临界距离l。训练集21 天的载客人数求平均值与测试集一天载客人数的对比结果，如图13所示。

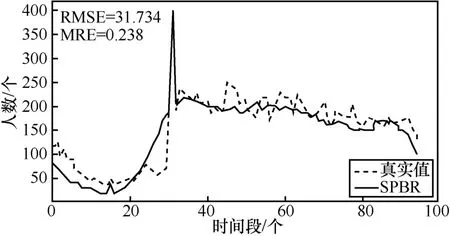
图13 训练集平均载客人数与测试集一天载客人数对比

对比图13 与图9 可知，训练集平均载客人数与实际误差较大，远远不如通过SPBR 预测数据准确；当SPBR 输入段和预测段距离增加，预测误差大于训练集平均值误差时，可用训练集平均值代替SPBR 预测。SPBR 预测误差随输入段和预测段距离的变化如图14 所示。

当预测距离大于6 时，基于SPBR 预测的RMSE和MRE 都大于测试集平均值的误差。式(13)的具体形式可写为

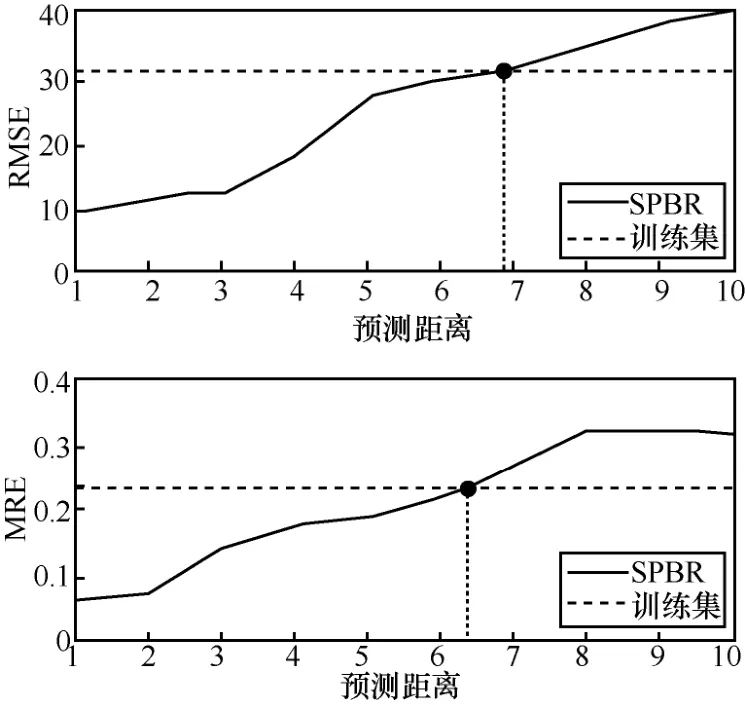
图14 SPBR 预测误差

载客人数矩阵X∈100×96，为了保证数据形式的一致性，与载客概率矩阵相同，将X∈100×96转化成X∈9600×9600，可求得回报矩阵R=XQG，即矩阵对应位置元素相乘。

4.2.2 TMDP 推荐结果分析

当预测距离大于6 时，SPBR 预测的误差大于历史平均误差，所以在TMDP 推荐时，折扣因子要尽可能减少预测距离大于6 的阶段所占比重。根据MDP 原理，当预测距离为7 时的回报项为γ6R(s)，因为0.56=0.015≈0，所以令折扣因子γ=0.5。获取TMDP 的五元组(S,A,Psia,γ,Rsia)各个参数。

通过策略迭代求得状态−值函数V(s)达到最大值的最优策略函数π*(s)。

TMDP 推荐结果策略如表4 所示，si(0≤i＜100)表示出租车所在区域，Tj(0≤j＜96)表示出租车所在时间段。策略为1 表示出租车空载状态下TMDP 建议在当前区域等待。策略为2表示出租车空载状态下TMDP建议去往其他区域寻客。基于表4 的推荐策略，每个状态可得到的最大期望回报矩阵如表5 所示。

表4 TMDP 推荐结果策略

表5 TMDP 最大期望回报矩阵

每个区域每个时间段都有对应的最大期望回报，但有些区域的期望回报普遍较大。例如，经过推荐，s2和s99各时间段的回报都要高于其他区域。因为每个载客区域由载客点聚类得到，区域s2和s99的聚类中心点分别为(116.42224,39.89670)和(3991071,11645097)。

载客热点s2在北京站附近，s99在中国国际贸易中心附近，这些区域客流量大，出租车处于空载状态时只需选择在当前区域等待就会得到最大的期望回报。该例在一定程度上证明了TMDP 推荐符合实际情况。

采用历史平均回报作为对比，分析TMDP 推荐的效果，令判断条件为

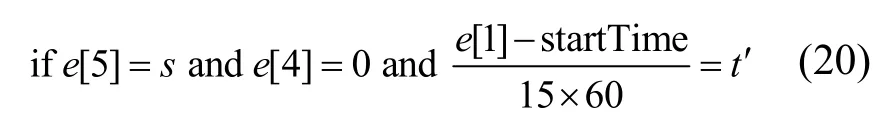
可从历史数据中求得与行为无关的状态转移概率矩阵P'，当最大预测距离为6 时，对应TMDP中折扣因子γ=0.5，定义矩阵Z为

其中，R为回报矩阵；Z∈ℜ9600×9600，其每一行代表从相应状态出发经过6 次转移分别到9 600 个状态产生的期望回报。将Z的每行所有元素相加得到Z′∈ℜ9600×1，表示从每个状态出发总的期望回报，为了方便对比，将Z'转换为历史期望回报矩阵H，如表6 所示。

表6 历史期望回报矩阵

为了整体分析TMDP 的推荐结果，分别求表5和表6 中每列的平均值，得到TMDP 所有区域平均期望回报∈ℜ96×1和历史所有区域平均期望回报∈ℜ96×1，和的对比如图15 所示。

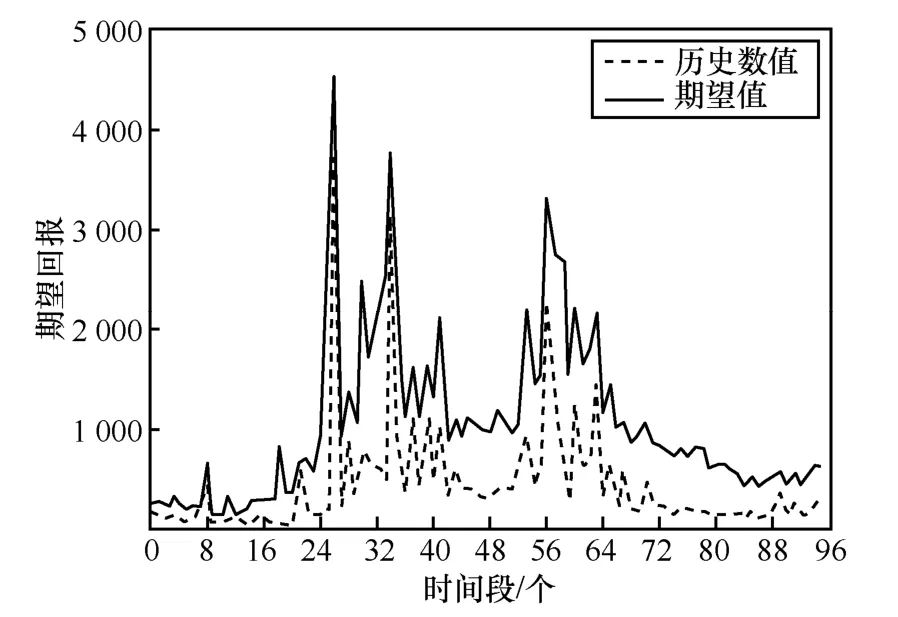
图15 区域平均期望回报

在每个时间段，基于TMDP 推荐的载客策略平均期望回报普遍大于历史平均期望回报。由式(22)计算，结果表明基于TMDP 推荐的平均一个时间段（15 min）的回报增长率为35.9%。

综上所述，通过TMDP 推荐的载客策略，出租车在15 min 内的预期回报相比原来平均增长了35.9%，所以TMDP 能够使司机收入得到大幅提升。由于TMDP 推荐是基于历史载客数据，因此TMDP推荐的实质是将挖掘出的历史乘客信息与出租车行为进行有效分析，实现对出租车的合理调度，有助于降低出租车空载时间、提高出租车司机收入、缓解交通拥堵等。

5 结束语

本文的研究内容包括预测和推荐两部分。针对乘客预测，本文提出了SPBR 算法，在传统出租车载客预测算法的基础上考虑了数据的时间序列性，将循环神经网络运用到载客预测中。通过仿真分析，与SVR 算法、CART 算法和BPNN 算法进行对比，验证了SPBR 算法预测的准确性；通过与一次性多段预测比较验证了多次分段预测的合理性。针对载客推荐，与以往只考虑即时收益不同，本文研究了如何对出租车载客进行长远规划从而最大化期望回报，结合马尔可夫决策过程和出租车推荐系统的特点，提出了分时马尔可夫决策过程实现推荐。仿真结果表明，采用推荐策略的出租车期望回报相比历史期望回报在一个时间段内提升了35.9%。