分布式排队中退避树的深度优先遍历算法

王文鼐，张延贺，吴炜，柏琛，王斌

（南京邮电大学通信与信息工程学院，江苏 南京 210003）

1 引言

分布式排队（DQ,distributed queuing）是综合了时分复用（TDM,time division multiplex）和随机多址接入（RMA,random multiple access）2 种手段的媒质访问控制方法，其最初目标是高效解决有线电视电缆的多站接入冲突[1]。由于DQ 的吞吐性能和重载稳定性接近理想的无冲突M/D/1 排队系统[2]，其近年来被扩展到各类无线接入网，特别是终端密度高、业务突发性强、功能复杂度低的物联网（IoT,Internet of things）[3-8]，甚至被视为ALOHA 技术的终结者[9]。

DQ 系统包含一个集中式协调者和2 个分布式虚拟队列，分别为争用请求队列（CRQ,contention request queue）和数据发送队列（DTQ,data-transmit queue）[1]。CRQ 的离队站点随机争用共享信道，争用成功时进入DTQ，否则返回CRQ 退避。DTQ 的离队站点以TDM 方式无冲突地占用信道。共享信道的争用状态由协调者监测和反馈，其功能可以由小区制基站或接入点（AP,access point）实现[3-4]，也可以由自组织网络的簇头临时实现[5]。DQ 时隙结构和争用信号方式有很大的灵活性，能适应不同的应用环境。

文献[3]针对长期演进技术（LTE,long term evolution）物理随机接入信道（PRACH,physical random access channel）提出了一种基于前导信号的DQ 应用方案，发现用户设备的接入阻塞率、吞吐量和能耗都有显著优势，尤其是在重载时阻塞率保持为零。文献[4]发现DQ 用于窄带物联网（NB-IoT,narrow band Internet of things）时，在保持100%接入成功率的同时，通过资源分组能进一步减少接入时延。文献[5]针对IEEE 802.11 WLAN 提出了一种基于请求发送（RTS,request to send）控制帧的DQ争用时隙方案，发现吞吐量至少能提升25%。文献[6]将DQ 用于Ad-Hoc 网络，发现重负载时DQ 吞吐量可比传统的IEEE 802.11 技术提高85%。文献[7]针对LoRaWAN 设计了一种DQ 验证原型，估算发现，在增大TDM 时隙的占比后，相同性能条件下能将接入容量从1 500 个终端提高到5 712 个终端。本文的先期工作提出另一种DQ 结合LoRaWAN 的方案，通过数值仿真发现，与现有技术标准的接入方案相比，吞吐量可增大2.6 倍，500 个终端并发时的平均时延可降低54%[8]。

相比于ALOHA，DQ 表现出全方位的性能优势，原因有以下2 个方面：1)DQ 将争用冲突压缩在相对短时长的争用时隙；2)DQ 采用树型退避算法以指数形式递减并发站点数。相比于早期的树型随机多址[10]，DQ 分配了多个争用时隙。争用时隙数目m越大，冲突解决时效性越好，但相应的时间开销也越大，反而会降低有效吞吐量。文献[2]的理论分析发现，m=3 是较好的折中条件。文献[8]的数值仿真发现，m=3 这一条件仅适用于中等规模的多站并发。在不增大m的前提下提高冲突解决时效，目前尚未见公开报道。

DQ 调度的重载性能稳定，功能相对简单，对以ALOHA 技术为基础的物联网接入等新型业务有很大的应用潜力[9]，因此受到研究者的关注。本文分析DQ 退避树遍历的计算优化，以进一步提高冲突解决时效性，研究用深度优先方法代替传统的广度优先方法。

2 DQ 工作机制

2.1 系统组成与时序

ALOHA 完全由数据站组成[10]，而DQ 系统则引入一个集中式协调者站点。为叙述方便，以下假设协调者功能部署在小区中心基站或AP，数据站为小区终端，DQ 的调度对象是并发终端至基站上行的数据传输。

DQ 以时分复用方式共享信道，重复的DQ 周期包含上行争用时隙（CS,contention slot）和数据时隙（DS,data slot），以及协调者至所有终端的下行反馈时隙（FS,feed-back slot）[1]。CS 嵌套m个小时隙/子时隙（MS,mini-slot）。DQ 时域共享信道的时隙划分结构如图1 所示。

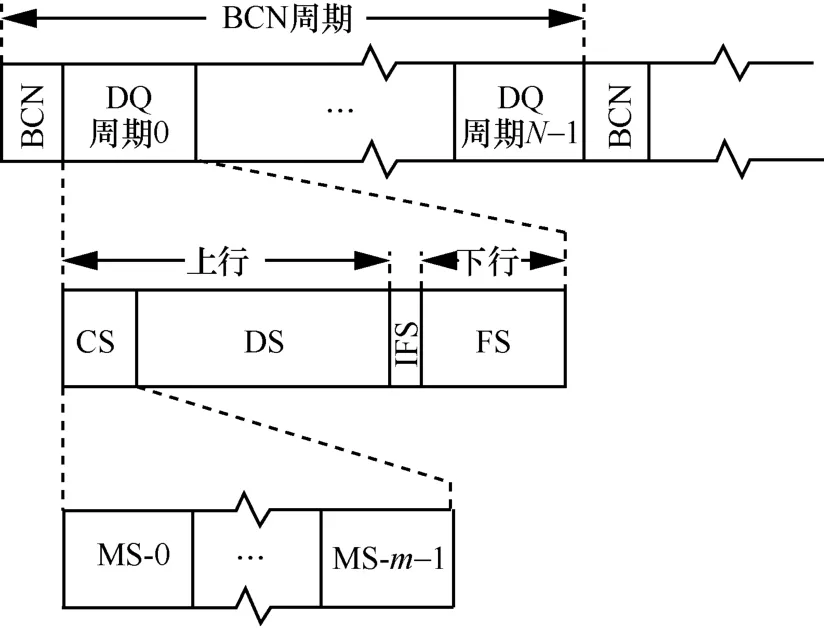
图1 DQ 时域共享信道的时隙划分结构

图1 中，信标（BCN,beacon）广播起到定时同步的作用，帧间空隙（IFS,inter-frame space）用于容纳上下行传播时延。N个DQ 调度周期构成一个BCN 周期，N值由BCN 广播通告或者动态配置。

在一个BCN 周期内新到的终端发送请求，并推至下一个BCN 周期。争用时隙包含m个子时隙供终端随机争用，其中m≥2。一个DQ 调度周期只包含一个数据时隙，多个争用成功的终端顺序排队占用多个DQ 周期内的DS。

静态系统配置固定的子时隙数m，以及固定时长的MS、CS、DS 和FS。

2.2 分布式排队过程

为方便说明，DQ 终端标识记为k，k∈[0,Kn−1]，其中，Kn为第n个DQ 周期内并发争用DS 的终端总数，n∈[0,N−1]。争用终端k在m个MS 中以等概率随机选择一个发送请求帧或请求信号，选中的MS 索引记为rk，rk∈[0,m−1]。

协调者监听CS 内所有MS。当仅有一个终端占用MS 时，由于可以正确恢复出请求信息，因此易被判定为争用成功；当2 个及2 个以上终端占用MS 时，由于存在互干扰，因此易被判定为争用失败；当没有终端占用MS 时，因无载波信号而易被判定为空闲。

协调者在FS 以广播方式反馈MS 的监听结果或MS 状态，记为ai，i∈[0,m−1]。不失一般性地，设ai=0 表示空闲，ai=1 表示争用成功，ai=2 表示冲突或争用失败。

所有争用终端在每个DQ 周期FS 接收来自协调者的ai反馈结果，独立计算式(1)。

其中，G为争用成功的终端个数，C为争用失败的终端组的个数，gk为终端k争用成功时的次序号，ck为终端k争用失败时的次序号。当ai=n时δ(ai,n)=1，否则δ(ai,n)=0。

协调者在监听MS 状态的同时，同理计算G和C，并分别累加到由其集中维护的DTQ 长度LT和CRQ 长度LC。

如果ai=1，且rk=i在G个成功者中的次序为gk，gk∈[0,G−1]，则终端k进入DTQ 队尾，并由该终端自身记录其在DTQ 中的位置为

其中，LT由协调者统计和广播通告，其随G递增、随DQ 周期递减；gk是对ai的统计结果；pk随DQ周期递减。

如果aj=2，且rk=j在C个失败组中的次序为ck，ck∈[0,C−1]，则所有选中j的终端返回CRQ 队尾，并由这些终端自身记录其在CRQ 中的位置为

其中，LC由协调者按DTQ 相同的方法计算和通告，ck是对ai的统计结果，qk随DQ 周期递减。

式(1)～式(3)的计算依赖于协调者在FS 的广播反馈，FS 和m个MS 的总时长是分布式排队的系统开销。

2.3 冲突解决过程

队列CRQ 和DTQ 在DQ 中并无物理实体，排队功能分布在各个终端，所以是虚拟的。LT和LC由协调者在FS 中随ai一起广播给所有终端。显然，每个DTQ 位置上最多只能有一个终端，而每个CRQ 位置上的一组终端至少有2 个成员，它们是后继DQ 周期参与争占的终端数，即Kn。

以m=2 为例，设初始时K0=18，有LC=0，LT=0。在初始DQ 周期T0，假设2 个MS 各有9 个终端选中，则G=0，C=2，LC=2，LT=0。由式(1)～式(3)可知，协调者将队列长度LC和LT以及MS 状态以广播方式反馈给所有终端，冲突终端依此分为两组退避重入CRQ。结果是，CRQ 队首2 个位置各有一组终端，每组各有9 个终端。因此，在DQ 周期T1和T2，有K2=K3=9。

在DQ 周期T1，设2 个MS 各有5 个和4 个站点，可得G=0，C=2，LC=3，依次类推。变量Kn、G、C、LT、LC，以及终端k在队列中的位置pk和qk，取决于该终端选取MS 的具体情况。图2 描述了其中一种可能的过程。其中，矩形框表示小时隙，其中数字表示争用终端的数量，粗边框表示冲突，细边框表示成功；细箭头线表示终端组的树型分割，粗箭头线表示树的遍历次序。

图2 DQ 冲突退避与解决的过程示例

图2 中，2 个一组的矩形框表示2 个MS，中间数值表示并发争用的终端数。争用失败的终端按所选MS 的序号，进入CRQ 队尾退避等待和重新争用。从图2 给出的特定时序可以看出，在第8 个DQ 周期T7，冲突得到部分解决，LC开始减小，DTQ有成功者入队。

需要说明的是，图2 对应于终端以大概率平均选择MS 的情况，如果终端选择出现随机偏离，将增加退避树的深度及调度的遍历时长。

3 改进算法

3.1 树遍历的优化机会

DQ 冲突退避采用了树型分割方法对一组终端迭代细分，对应的遍历次序具有宽度优先搜索（BFS,breadth first searching）特点。当初始终端数远大于MS 配置数，即K0＞＞m时，到达冲突解决的叶节点需要遍历大量存在冲突的树的中间节点。

从图2 可以直观地看出，在相同MS 配置数的情况下，换用深度优先搜索（DFS,depth first searching）可以更快地到达冲突解决的叶子节点，竞选出DTQ的入队终端。图3 描述了一个可能的遍历过程。

图3 DFS 遍历冲突解决叶子节点示例

图3 中，虚边框表示MS 未被任何终端选中，即空闲状态。为简化绘制，图3 主要给出DFS 搜索至前2 个叶子节点的过程，省略了后继的遍历细节。

从图3 可以直观地看出，在第4 个DQ 周期（T3）得到2 个DTQ 入队终端，这比BFS 提前了4 个DQ周期。因此，基于DFS 的CRQ 退避规则能更快地解决争用冲突。

3.2 算法设计

改进算法沿用与BFS 相同的MS 监听和DTQ调度规则。协调者在得到MS 状态后，同样将LT、LC和MS 的状态反馈给所有终端，同时进行队列长度更新。

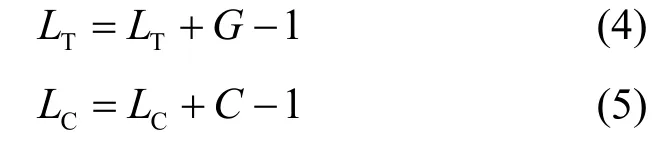
其中，G是争用成功的MS 个数，C是冲突失败的MS 个数，减1 对应于队首离队情况。另外，队列长度减至0 时不再减小。

DFS 的作用主要体现在冲突时终端的CRQ 位置更新和计算。BFS 中，终端返回CRQ 队尾，而在DFS中则进入CRQ 队首以获得优先重试机会。这就要求在CRQ 中排队的终端后移位置，具体计算式为

其中，C由各终端独立地从FS 反馈信息计算得出，减1 计算对应于排队前移。

对于从CRQ 离队但争用失败的终端k，返回CRQ 的位置就是计算前述的变量ck，即终端所选rk在C个冲突MS 中的次序。算法1 给出了分布的终端独立执行DFS 退避的伪代码，其中，a[i]=0、1、2 分别表示MS 处于空闲、成功、冲突状态，r=0,1,…,m−1 表示终端所选MS 的索引号，q表示终端在CRQ 中的位置。

算法1 中CRQ-POS 针对退避等待和争用状态分别处理。第2)～9)行是已处于退避等待终端的位置后移，第12)～14)行及函数DTQ-POS 是对争用成功计算DTQ 位置，第15)～22)行针对争用失败按序进入CRQ 队头。需要注意的是，以上伪代码省略了MS 为空闭和通信出错的处理。

CRQ-POS 的唯一预设条件是在调用CRQ-POS之前，当终端CRQ 位置q=0 时，该终端独立地以一致概率在区间[0,m−1]生成随机整数，并记录在参量r中。

算法1 中第13)行调用的函数DTQ-POS 的主要功能是确定争用成功的终端在DTQ 中的位置，按式(2)计算。

相比于BFS，以上基于DFS 的改进算法的复杂度仅增加了终端在CRQ 队内排队等待的后移计算，即算法CRQ-POS 的第2)～9)行。如图3 所示，这种极小量的计算开销带来了改善系统吞吐性能的预期。当然，这里的后移计算，其前提是CRQ 队内的退避终端要持续不断地监听和处理来自协调者的反馈信息。

4 吞吐性能对比分析

4.1 吞吐量最大条件

图1 表示的DQ 周期中，将MS 的时长记为TM，DS、FS 和IFS 的时长分别记为TDS、TFS和TIFS，则共享信道的吞吐量为

其中，u表示有数据传输的DS 总数，v表示无数据传输的DS 总数。

设一个BCN 周期正好容纳所有终端的数据发送，则u=K0，N=u+v。

从式(7)可知，v和m越小，S越大。但m越小，对应于CS 内嵌的MS 越少，终端争用的冲突概率越大，导致v越大。所以，以吞吐量最大为目标，最佳m需满足

4.2 完全树的对比分析

图4 给出了K0=32 时冲突退避构成完全二叉树的特例。图4(a)对应BFS，图4(b)对应DFS。

图4 K0=32 时冲突退避构成完全二叉树的特例

图4 中，树中圆节点表示MS 冲突的情况，方形叶子节点表示冲突解决。树遍历过程只涉及圆节点，实心圆表示v的贡献项，空心圆表示因DS 内有数据传输而对v无贡献的情况。

图4(a)树根对应树的第0 层，初始时DS 无数据发送，v=1，2 个MS 各分16 个终端；第1 层2 个中间节点，对应DS 同样无数据发送，所以v=1+2=3；第3 层，v=15；第4 层左侧第1 个节点仍有冲突，v=16；第5 层为2 个叶子节点，所以第4 层后继节点遍历时DS 有数据发送，它们对v无贡献。因此可得v=16。

图4(b)树根至最左侧叶子节点，深度为4，其中DS 无数据发送，所以v=4。该树的后继遍历中，所至中间节点均有对应的叶子节点，如图4(b)中序号为1～16 的节点所示，它们对v无贡献。因此可得v=4。

以上针对K0=2L的完全二叉树，从图4(a)表示的BFS 遍历可得，v=2L−1=16，从图4(b)表示的DFS可得，v=L−1=4，其中，L=lbK0为树的深度。对于m≥2 的一般情况，可得L=logm(K0)，且

对于DFS，从式(13)可知，因为m＞1，所以dvDFS/dm＞0。代入式(8)，左侧总是大于0，所以吞吐量最大条件是mDFS_MAX=2，有

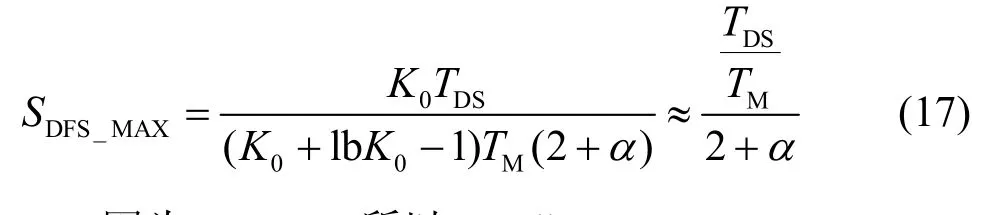
因为K0＞＞2，所以K0+lbK0−1≈K0。

定义加率比f=SDFS_MAX/SBFS_MAX，则有

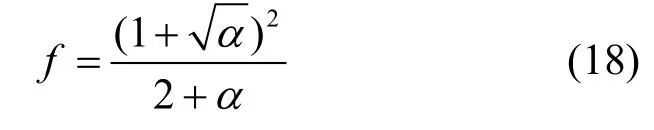
易得，当α=4 时，有最大加速比f=1.5。

4.3 一般随机树的对比分析

以上推算虽然只适用于完全树的特例，但DFS性能优于BFS 的结论适用于一般性情况。这是因为，当K0＞＞m时，终端均匀争用各小时隙的概率最大，完全树分布对性能贡献权重也最大。此外，一般随机树的情况可等效于完全树的随机重构。

从K0=mL完全树出发，随机选取一个叶子节点，将其修减，得到K0−1 的随机树；将其移接到其他随机选取的叶子节点，则得到一个非平衡的随机树。修减一个叶子节点，对变量v至多贡献一次正计数。移接一个叶子节点，将对BFS 的v增加一个计数，而对DFS 的v，只在前驱遍历LT=0 时才有一次加1 的贡献。总体上，完全树随机重构后，基于DFS 的冲突解决仍然快于BFS。

当然，完全树随机重构后，式(16)和式(17)最大吞吐量条件会存在偏离。相应地，式(18)给出的加速比只可视为一个近似估计。下面，通过随机化网络仿真说明更一般的情况。

5 数值仿真验证

5.1 仿真软件设计

如前文所述，传统基于BFS 的DQ 调度和本文设计的基于DFS 的改进算法采用相同的时域信道划分结构和相同的DTQ 排队规则，而CRQ 排队规则有所差别。因此，本文基于开源NS-3 离散事件仿真软件，设计了的状态机和事件类型，DQ 仿真的状态迁移与事件如图5 所示。

图5 DQ 仿真的状态迁移与事件

图5 中的仿真对象类DqChannel 按固定的定时事件分别调用协调者和终端网络接口的接口函数，完成信标帧的收发、CS 争用与监听和反馈帧Fbp的收发。

协调者和终端网络接口派生于对象类ns3::NetDevice，DqChannel 派生于ns3::Channel。终端在争用接入（CsAcc）状态随机选占一个小时隙（SelectMs），协调者统计争用请求（RxCres）并在状态FsBcast 发送反馈帧（TxFbp）。所有终端数据发送完成后，协调者再次发送信标，以支持连续多次仿真。

终端网络接口在每个BCN 周期内发出一次数据帧，在状态FsListen 收到反馈帧后，依据DQ 规则进行CRQ排队（CrqWait）或DTQ排队（DtqWait）。终端属性p和q分别记录终端在DTQ 和CRQ 中的位置，并利用NS3 的变量跟踪机制提供监测和统计。当p=0 时，终端迁移至数据发送状态DsTx，在紧随其后的DQ 周期的DS 发送数据TxData，然后进入状态BcnListen 等待下一轮仿真。

针对DQ 调度性能的仿真，图5 设计的简化模型假设所有数据长度固定不变，时长均为TDS。而共享时域信道的划分由DqChannel 相应属性提供配置接口。本文仿真实验设置TDS=0.3 s，TBCN=TFS=0.1 s，TIFS=2 ms，TM=0.01 s，相应地，TF=0.4 s，α=40。

5.2 争用时隙优化条件

图6 和图7 分别给出了BFS 和DFS 中CRQ 和DTQ 排队长度随时间变化趋势。

图6 描述了BFS 解决信道争用的排队长度变化。初始时刻（T=0），并发终端数K0=1 000，DTQ长度LT=0，CRQ 长度LC=1。

图6 BFS 中DTQ 和CRQ 排队长度随时间变化趋势

从图6(a)的LT曲线可以看出，LT随时间增加先增大，达到最大值后线性递减至0。m=2 时，210 s左右LT达到最大值，650 s 左右LT减小至0。m=20时，LT达到最大值和0 值的时间分别约为210 s 和600 s，LT达到最大值时间对应于LC=0。这是因为，CRQ 内退避终端清零时，后继没有入队而只有出队的DTQ 只会随时间递减。

从图6(b)的LC曲线可以看出，随着时间增加，LC先增大，达到最大值后再逐渐减小到0。m值越大，最大值和0 值出现时间越小。m=2 时，250 s 左右LC达到最大值，650 s 左右LC减小至0。m=20 时，LC达到最大值和0 的时间分别约为30 s 和210 s。

从图6 可见，当m=4、5、6 时，LT=0 的时间最小，即K0个终端全部完成数据发送的时间最少。根据式(15)，吞吐量最大的理论条件是mBFS_MAX≈6，这与仿真结果是吻合的。

图7 描述了相同初始条件下DFS解决信道争用的排队长度变化，其中LT的变化趋势与图6 相似，但LC的变化幅度比图6 小一个数量级。因曲线重叠，图7(b)分别给出了m=2、3、20 的LC时变曲线。同样的规律是，当LC=0 时，LT达到最大；当LT=0时，K0个终端全部完成数据发送。

图7 DSF 中DTQ 和CRQ 排队长度随时间变化趋势

从图7 可以看出，m=3 的DTQ 排队长度LT最先减少至0，这与式(17)的估算结果吻合。

文献[2]在忽略CRQ 与DTQ 的相互耦合的情况下，为传统DQ 给出的乐观估计是，吞吐量最大条件是小时隙配置m=3。依据仿真实验，传统DQ 最佳条件应为m=4，基于DFS 的改进算法的最佳条件为m=3。这是因为，DFS 能更快地搜索到退避树叶子节点，为冲突解决提供同时进行数据传输的机会，减少DS 空转概率。

5.3 吞吐性能对比

本节以小时隙最佳配置为条件，对DQ 吞吐性能随并发终端数的情况进行随机实验，统计结果如图8 所示。

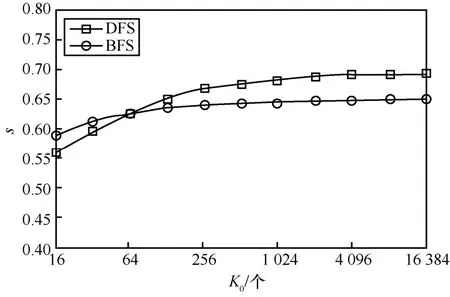
图8 归一化吞吐量随并发终端数的变化

图8 所示的仿真中，DFS 中设置m=3，BFS 中设置m=4。仿真总时长设为8×105s，针对K0=16 384，得到10 组BCN 周期；针对K0=16，得到9 000 组以上BCN 周期。归一化吞吐量为，其中Ttot为所有BCN 周期完成的仿真时间。

当K0=16 384 时，DFS 和BFS 仿真中的Ttot平均值分别为7 085.291 s 和7 537 s。对应ALOHA，按G=K0(Ttot/TDS)−1计算归一化负载分别为0.96 和0.69。依文献[10]，可得归一化吞吐量分别为0.141和0.173，均小于理论上的最大值0.184。

从图8 可见，DQ 的归一化吞吐量大于0.55，重负载时超过0.65，反映出远好于ALOHA 的稳定性。当并发终端数K0＞64 时，相比于DQ 原有算法，改进算法的吞吐量有最大6%的提升，接近信道物理容量的70%。表1 给出了BFS 和DFS 算法下所有终端完成数据发送的总时长及加速因子计算结果。

表1 BFS 和DFS 算法下所有终端完成数据发送的总时长及加速因子计算结果

6 结束语

分布式排队综合了ALOHA 随机多址和时分复用的技术手段，通过树型退避方法压缩多终端接入的连续冲突概率，使共享信道的有效利用率得到大幅提高。共享信道的争用时隙配置与优化是DQ 技术的应用关键。本文分析了DQ 工作机制，针对争用请求队列采用的宽度优先遍历树，设计了基于深度优先的改进算法，并给出了理论和仿真的分析结果，证明了改进算法可以进一步提高吞吐性能。此外，本文采用了随机树分析法估算出DQ 争用时隙数的最佳配置条件，并通过仿真实验进行了验证。本文预设DQ 系统具有理想的定时同步性能，这在实际应用中，特别是应用于因休眠节能而不能持久同步的物联网时，是值得进一步深入探索的问题。