界面追踪和拉格朗日粒子追踪耦合计算方法

刘 静，殷 义，时明伟

（北京航化节能环保技术有限公司，北京100176）

根据研究目的和需要可以将气液两相流动的数值模拟方法分为两大类。 （1）拉格朗日粒子追踪方法：这种方法发展历史长，应用也比较广泛。 拉格朗日粒子追踪方法也称为离散颗粒模型， 颗粒被看作离散相，而气相被视为连续相。这种方法对每个颗粒与气体以及颗粒与颗粒间的作用都详细考虑。 对于离散颗粒的破碎、 蒸发等物理过程都有相应的子模型进行描述。 （2）界面追踪方法：这是一种较新的研究两相流动的方法。 该方法可以通过计算两相交界面的运动，再现液相在气相作用下的详细雾化过程，从而达到研究气液雾化机理的目的。 目前常用的有体积分数方法和Level Set 方法等。

本文首先分别采用以上介绍的两大类方法对射流和液滴进行了计算，针对两种方法的优缺点，提出了新的改进的计算方法。 结合实验测量结果,对采用改进方法的计算结果与两种常用计算方法的结果进行了对比分析。

1 计算方法

1.1 拉格朗日粒子追踪方法

拉格朗日方法中，气相控制方程为三维N-S 方程。液相采取拉格朗日颗粒跟踪方法。液滴对周围气相的影响表示为气相方程中的源相S。 而气相对液相的影响则通过在计算液滴状态的过程中， 当用到气相参数时直接采用液相所属当地网格的气相参数来实现。

三维气相N-S 方程为：

式中: U—守恒变矢量

F—x 方向的无粘矢通量

G—y 方向的无粘矢通量

H—z 方向的无粘矢通量

Fv—x 方向的粘性矢通量

Gv—y 方向的粘性矢通量

Hv—z 方向的粘性矢通量

t—时间变量，s

x—x 坐标方向，m

y—y 坐标方向，m

z—z 坐标方向，m

S—液相影响源相矢量

液滴在运动过程中受到了空气阻力和重力，液滴单位质量受力用下式计算：

式中：下标g—气相参数

下标d—液相参数

u—速度矢量，m/s

r—液滴半径，m

g—重力加速度，m/s2

阻力系数CD计算公式为：

气相雷诺数Re 为：

式中，μ 为气体黏性系数。

单个液滴的运动速度计算公式为：

得到液滴的运动轨迹计算公式为：

液滴在运动过程中的雾化和蒸发由相应的子模型来描述。本文中只考虑雾化过程，液滴的雾化采用K-H 和R-T 混合雾化模型。

计算流程如图1 所示。

图1 计算流程示意图

1.2 界面追踪方法

假定在多介质的界面上，压力和速度为常数，而其它物理量在界面上可能存在着间断。 以此假设为出发点， 可以得到多介质可压缩流动的一维模型方程组，具体推导过程可以参考文献[4]、[6]、[7]。

简便起见， 这里给出采用体积分数形式描述的一维多介质可压缩流动的欧拉方程组：

各介质的状态方程采用如下形式：

式中：ρ—密度，kg/m3

u—x 方向速度，m/s

p—压强，Pa

e—单位质量的内能，kJ/kg

E=e+u2/2，单位质量的总能量，kJ/kg

N 为介质种类总数，Y（i）为第 i 种介质的体积分数。 在一个网格中，N 种介质的体积分数总和为1。

若已知各组分的物理量 ρ（i），u（i），p（i），γ（i），p∞（i）。 各组分压力与网格压力相等 p=p（i），i=1，…，N。 网格中的平均物理量计算方法为各组分物理量的体积加权平均值。

状态方程可表达为

求解方法采用的一维Lagrangian-Remapping 型PPM（Piecewise Parabolic Method）方法。 具体可分为以下四步：（1）各物理量的分段抛物差值；（2）近似黎曼问题求解网格边界上时间平均的压力和速度；（3）拉格朗日方程组推进求解；（4）将物理量转换到静止的欧拉网格上。 对于三维方程的求解采用Strang 分裂方法， 将多维的求解转化为多个一维方向交替计算。 采用Strang 分裂计算简单而且有助于编制并行效率很高的程序，对开展大规模并行计算很有帮助。

2 计算结果和分析

2.1 计算条件

算例一：矩形超声速风洞长762 mm、宽152 mm、高 127 mm，来流 Ma 为 1.94，流场总温 T* 为 533 K，总压P* 为206 kPa，喷注器为直流形式，出口直径d为0.5 mm，安装在风洞底部，动压比为10。

算例二：液滴在激波管中发生破碎，气流速度为432 m/s，液滴直径为2.6 mm。 该工况为文献[9]中的实验工况，对于该工况文献[9]还给出了实验结果，以便于对比分析。

2.2 拉格朗日粒子追踪法计算结果

图2 为三维喷雾流动的液雾分布图。 当液体射流从喷嘴喷出后不久，在与高速气流的相互作用下，一边不断地发生破碎生成新的液滴， 一边随着气流向下游运动。

图2 液雾分布图

图3 为液雾雾化过程中的滴径分布图。 可以看出，当等于喷口直径的大液滴从喷口喷出后，在KH 不稳定波的作用下， 逐渐从上面剥离出直径较小的液滴，并跟随气流向下游运动，形成液柱后的一片液雾， 此时大液滴在运动过程中随着小液滴的逐渐剥离直径也慢慢减小，这就类似于液柱在刚喷出后，由于气流的作用会从其上面剥离走一部分小液滴。而当大液滴运动到其累计时间大于破碎特征时间时，R-T 不稳定模型此时也加入竞争。 在此之后，大液滴进一步被剥离或破碎成较小的液滴， 液雾外围的液滴直径大于靠近壁面的液滴。

图3 液雾雾化分布图

采用拉格朗日粒子追踪法，优点是计算量较小，占用的计算存储资源少。但在计算雾化子模型中，需要引进一些计算经验常数， 有时在计算中经验参数的选择对计算结果影响较大。

2.3 界面追踪方法计算结果

图4 为射流从底部垂直于来流方向喷入燃烧室后的形态图。 可以看出，当射流从下底面喷出后，在来流的压力作用下， 圆柱流由刚喷出时的圆形截面迅速展开呈现一个拱形的包络面， 液柱在随着气流弯向下游的同时，由圆形截面展成了片状截面。可以看到在液柱迎风面距离下底面一定距离处有明显波动的起伏。 而在液柱的两侧由于气流对液体的剪切作用，呈现出一些条状的凸起，有一些大的液块已经脱离主液柱随流运动。

图4 射流形态对比图

对算例二液滴雾化过程也进行了计算。 在高速气体的作用下，液滴迅速雾化完毕。图5 为液体体积分数为0.01 的液滴雾化过程的等值面图。 当45 μs时，圆形的液滴被气流逐渐压扁，边缘被气流撕扯出一些不规则边缘；当75 μs 时，边缘上的液膜和凸起进一步被气流作用， 液滴被压得更扁；130 μs 时，液滴的凸起伸长，呈现规则的八角形；当时间达到170 μs 时，液滴已经伸展成一片状结构，且迎风面明显出现一圈规则的凹坑；到290 μs 时，凹坑处破裂，液滴完全分解成块状。

通过对比计算结果图与实验结果图（见图6）发现， 计算结果对液滴主体的追踪基本上与实验观测结果相一致， 但对于更加细小的液雾的追踪用目前的界面追踪方法就无能为力了。 因为细密的液雾已经达到了微米量级， 理论上来说要想捕捉这些细小的液雾， 需要比液雾直径还要小的网格分辨率才能实现， 而这对于目前的计算条件来说是不可能实现的。而且本文所采用的体积分数模型在计算过程中，本身对界面的捕捉并不是清晰的， 而是跨越了几个网格，所以这也是目前计算存在的局限性。

3 改进方法和计算结果

3.1 改进方法

图5 液滴二次雾化体积分数等值面图

图6 液滴二次雾化实验结果图

前面分别用界面追踪和拉格朗日粒子追踪方法对雾化过程进行了计算， 在对结果的分析过程中发现，界面追踪方法能够真实地再现雾化过程，是研究射流或液滴的变形破碎、 不同的因素对雾化结果的影响程度以及进一步的雾化机理分析的有效工具。界面追踪随着计算机技术的发展而不断发展起来，但它同样存在自身的不足之处， 比如为了精确的捕捉气液界面，需要在界面附近布置极细的网格。如果需要捕捉剥离的液滴，那么就需要更加细密的网格。在高速气流中，雾化后的小液滴通常是微米量级的，所以如果想对整个雾化过程（一次雾化和二次雾化）进行计算， 那么最小的网格尺度必须小于雾化后的小液滴的尺寸，可以想象，如果想捕捉整个液雾的分布，那么对网格的细密程度要求是极高的，这将造成巨大的计算量， 甚至可以说这样的计算是不经济也是几乎不可能实现的。 而拉格朗日粒子追踪方法是工程计算中常用的一种方法，它的优点是计算量小，以追踪多组典型的液滴分布来代替整个液雾的计算。它虽然不能对具体的雾化过程进行描述，但对于更关心液雾运动和分布等宏观现象的研究， 这种方法更具有优势。在拉格朗日粒子追踪方法中，对雾化过程的模拟用一些雾化模型来代替。 由于对雾化机理研究的缺乏， 有限的雾化模型并不适用于所有的雾化过程。特别是对于一次雾化过程，到目前为止也没有一个专门针对一次雾化的雾化模型可供使用。一般的做法是省略一次雾化， 认为在出口处一次雾化已经结束， 直接在出口处给出实验测量的液雾尺寸分布；或认为出口处液滴尺寸近似等于喷孔直径，即“Blob 模型”，总之都是一种近似。

为了更精细的模拟雾化过程， 综合两种方法的优缺点， 尝试把界面追踪和拉格朗日粒子追踪方法结合起来。 对于无法用雾化模型描述的一次雾化过程采用界面追踪的方法来直接模拟， 而对之后的雾化过程采用拉格朗日粒子追踪的方法。 这样做的好处是：（1）采用界面追踪的方法很好的解决了一次雾化过程的模拟；（2）用拉格朗日粒子追踪方法对雾化后细密粒子的追踪极大节约了计算网格， 提高了计算效率。这样做结合了两种方法的优点，而且避免了各自的不足之处。表1 对几种计算方法进行了对比。

表1 几种计算方法对比

界面追踪和拉格朗日粒子追踪方法在前面已经详细介绍过， 这里主要介绍一下两种模型在结合过程中的一些具体方法。 主要的问题是两种方法的转换方式，需要确定的重要参数如下。

（1）转换位置。 扫描全场，转换位置发生在同时满足以下条件的网格中： ①该网格内的液相体积分数大于0，具体量值可根据具体情况输入；②该网格正后方的网格非纯液体网格， 即该网格正后方是气体或气液混合区。若满足条件后，每个网格生成一个液滴组，其中所有的液体或部分液体转化为液滴。

（2）转化后液滴的初始速度。若相邻网格有纯液网格，则速度等于纯液网格的速度中最小的那个；若相邻没有纯液网格， 则按体积分数取当地气相网格速度的一部分。

（3）液滴初始位置。 生成该液滴的当地网格位置。

（4）粒子大小。 由二次雾化模型求得，若已知液滴直径，则液滴数也就可以得到。

（5）气液相对速度的计算。由前面得到的液滴速度，可以计算出转化液滴后当地气相的速度，从而得到相对速度。

（6）当地网格计算考虑剥离液滴带走的动能，并设体积分数为0，并相应地修改密度。

3.2 计算流程

图7 为耦合计算方法流程图。 由于界面追踪的计算时间步长远小于拉格朗日粒子跟踪计算时间步长， 所以在进行了若干步界面追踪计算后进行一次拉格朗日粒子追踪计算， 使二者的推进时间保持一致。拉格朗日粒子追踪计算完成后，将体积分数和气相场源相的变化传递给界面追踪流场计算。 如此交替计算，直至满足计算条件为止。

3.3 计算结果

对气流中的横向射流破碎和液滴雾化进行界面追踪和拉格朗日粒子追踪方法的耦合计算。 计算工况与前面相同。射流从喷注器喷出后，在气流的作用下迅速破碎成液块和小液滴。 图8 是两种方法耦合后的计算结果。 图8（a）是xy 向液雾分布，三角形和圆形的标记点分别表示的是实验测量拟合结果，三角形为阴影法的结果，圆形为PDPA 的结果。二者之所以出现差别， 是由于PDPA 捕捉到一些分布稀疏的用阴影法无法观察到的外围液滴， 所以PDPA 的穿透深度高于阴影法。 本文的计算结果对于液雾浓密区其穿透深度与阴影法接近。 而外围扩散的稀疏的液滴分布在液雾前端与PDPA 结果吻合， 后面有个别的液滴分布偏高于PDPA 的计算结果。 图8（b）显示的是xz 向俯视图。 液雾分布呈现中间浓密两侧稀疏的趋势。从整体来说，计算结果与实验测量结果基本吻合。

图7 耦合计算方法流程图

图8 液柱破碎液雾分布图

图 9（a）是图 8（a）中方框区域放大图。和图 9（b）纯界面追踪计算结果相比， 液柱的部分转化为液滴并随流运动。这也是耦合方法的优势所在，纯界面追踪在液柱部分模拟得很好， 但对于射流后部浓密液雾的计算却无能为力。采用耦合方法，能自然地根据射流特性计算出其穿透深度， 而不再需要像使用混合雾化模型时， 须给出液柱破碎时间判断标准或破碎点的判断标准。

图9 耦合法和单纯界面追踪法对比图

通过耦合计算， 对于液滴雾化的整个流场进行了数值模拟。前段母液滴采用界面追踪法进行计算，之后的液雾区采用拉格朗日粒子追踪方法进行计算。 图10 为计算结果与实验结果的对比。45 μs 时，开始有液雾从液滴上剥离生成；75 μs 时， 液雾继续发展，且由实验结果看到，液滴上下两侧的液雾浓度较中间区域偏高；随着时间的推移，母液滴生成的液雾越来越多，浓度也越来越大。由图11 可见，从始至终液雾始终产生于整个母液滴的边缘区， 也就是变形最剧烈的地方，液雾分布呈现环状。

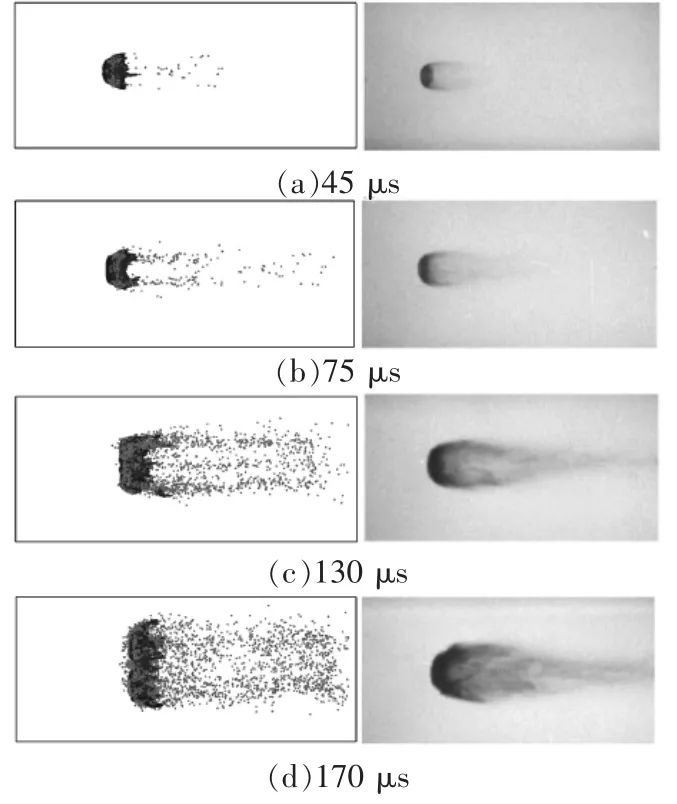
图10 二次雾化计算结果与实验结果对比图

图11 yz 向界面分布图

4 结论

为对雾化过程进行全面而准确的模拟， 结合界面追踪和拉格朗日粒子追踪的优点， 采用两种方法耦合的思路对射流破碎和液滴雾化进行了数值模拟。 射流破碎的计算过程在初始段采用界面追踪方法，比采用简单的一次雾化简化模型（Blob 模型）的计算结果更符合实际。与之前采用的混合模型相比，优点在于减少了经验参数的使用， 不再需要在使用混合雾化模型时给出经验破碎时间或破碎点的判断标准。液滴雾化的结果更显示了耦合方法的优越性，对于单个液滴雾化过程的模拟， 如果单独采用界面追踪或拉格朗日粒子追踪方法都不能够得到真实的雾化现象， 用耦合方法得到的计算结果与实验结果定性符合较好。 耦合方法结合了两种计算方法的优势，摒弃了不足，有助于研究一些对于两相界面形状和液雾分布都很重要的问题。