变式教学要多让学生“变”①

崔志荣

(江苏省东台市安丰中学 224221)

1 现象呈现

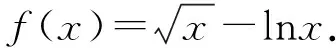
(1)若f(x)在x=x1,x2(x1≠x2)处导数相等，证明：f(x1)+f(x2)>8-8ln2；

(2)若a≤3-4ln2，证明：对于任意k>0，直线y=kx+a与曲线y=f(x)有唯一公共点．

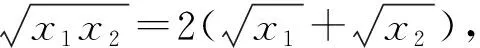
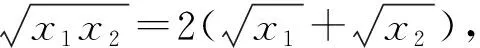
2 原因剖析

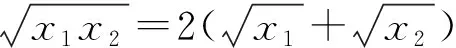
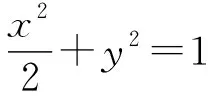
3 教学对策

怎样增强学生由二元等式主动分析发现其相关代数式取值范围的意识呢？笔者觉得仍可采用变式教学的手段，但不能是教师“变”，而应该是学生“变”.对于一个二元等式，要引导学生变换代数式，再分析求其取值范围，这能让学生明白一个道理：一个二元等式蕴含无数不等关系，我们能用所学知识求出一些有价值的代数式的取值范围；还要引导学生变换等式，让学生自己找出一些常见的二元等式，再研究其相关代数式的取值范围，能增强他们由“等式”主动转化到“不等式”的意识；最后再引导学生思考：为什么一个二元等式(或多元)中蕴含着众多不等关系呢？从而揭示问题的本质，提高学生的认知水平.若从基本不等式的新授课开始，经常这样变式教学，久而久之，学生的主动意识自然增强.

4 教学展示

针对以上分析，笔者就上述考题的第(1)小题设计了一个教学流程，并已用于实际教学，自感教学效果不错，故整理成下文，与读者交流研讨.

4.1 理性分析

问题1本次考试中的函数解答题的第(1)小题，同学们都有证明思路，但很多学生未能证明，请大家再思考：我们证明过程中疏忽了什么？

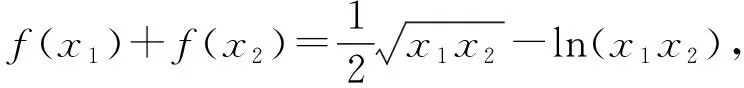
当然，该小题的教学不能就此结束，否则，以后再遇到类似的问题，学生还会犯同样的错误.上述逻辑反思，能够促进学生准确求出新元t的范围，但笔者估计不会起普遍性作用.若在教学中，加强学生理解二元等式(或多元)中蕴含不等关系的内涵，增强他们的转化意识，则会大幅降低该类问题的失误.

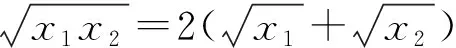
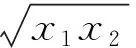
问题2揭示了一类数学题的本质，理解问题2虽对解题能力没有太大的提高，但能提高学生的认知水平，对解题思路的分析有指导意义.

4.2 “变”代数式

问题3对于等式ab=2(a+b)，其中a,b>0，则在关于a,b的所有代数式中，我们能求哪些常见代数式的取值范围(或最值)？

提出问题3，主要是让学生进一步感悟二元等式中蕴含相关代数式的取值范围；同时让学生回顾一些常规的基本不等式题；还能得到一些较陌生的基本不等式题.

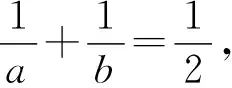
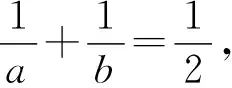
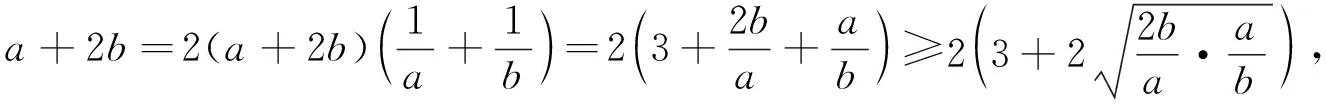
4.3 “变”等式

问题5求二元一次代数式(如a+2b)的取值范围，是高中数学常见的问题，除了上述等式ab=2(a+b)作为条件外，还有哪些二元等式可以作为条件？

问题5的目的，一是说明不同的二元等式可求同一代数式的取值范围；二是再加深理解一些常规的基本不等式题方法.

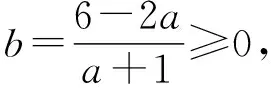
问题6同学们还知道哪些等式可以求a+2b的取值范围呢？

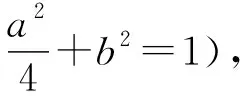
4.4 增强意识

问题7通过以上问题的思考，我们再反思一下这道函数检测题，怎样才能做到证明不失误呢？

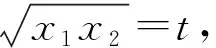
5 教学反思

变式教学毫无疑问是一种行之有效的教学方法，它能培养学生运用数学方法的灵活性，是教师日常教学常用的教学方法.但如果变式教学只是教师“变”，那还不能充分发挥其教学优势.教师还应多让学生“变”，让学生自己变换条件或提出新问题，不仅有助于学生深刻理解知识方法，使他们真正认识这些知识方法的本质，而不是在解题中机械套用；也有助于培养学生的问题意识，能让学生更深刻地认识一些数学问题，甚至能独立提出新问题、新观点；还有助于培养学生的主动运用意识，使学生面对一些数学现象，能联想其隐含条件，从而促进问题的解决.