神坛上的达·芬奇*——以达芬奇的数学手稿为中心

代 钦

(内蒙古师范大学科学技术史研究院 010022)

1 前言

列奥纳多·达·芬奇(Leonardo da Vinci，1452-1519)，是意大利文艺复兴时期最具创造力的艺术家、建筑师、工程师、科学家和数学家.他是意大利文艺复兴时期的象征，在那个年代里没有人能够有比达·芬奇更广阔的世界(1)[瑞士]雅各布·布克哈特.意大利文艺复兴时期的文化[M].何新，译.北京：商务印书馆，1997:40..由于达·芬奇为艺术作品蕴含思想和表现方法方面做出的开创性的划时代的贡献，人们认为达·芬奇是新观念的创始人，揭示艺术家是沉思与创造的思想家，并非是仅按每天涂抹的面积计酬的工匠.“16世纪种种关于艺术家的尊严的观念，显然都可以追溯到他所树立的榜样.”(2)黄才郎.西方美术辞典[M].北京：外文出版社，2002：480.达·芬奇没有某一科学技术领域的正式出版的著作，他关于解剖学、生物学、数学、物理以及力学方面的研究成果留在其浩瀚的手稿和笔记中.

达·芬奇于1452年4月15日出生在意大利皮斯托亚地区芬奇镇.他母亲卡泰丽娜(15岁)与职业公证人、贵族男子瑟·皮耶罗·达·芬奇(25岁)未婚生下达·芬奇.因为卡泰丽娜处于社会底层，被达·芬奇家族打发走之后与他人结婚.达·芬奇在其爷爷家成长，他父亲后来先后娶了4位妻子，为达·芬奇带来了13位同父异母的弟弟和妹妹.迄今为止，尚未发现达·芬奇在芬奇镇生活16年的详细历史记载.仅有的信息是“在学习计算法的几个月里，他获得了长足的进步，因此不断地向老师提出质疑并与老师探讨难点，但通常老师也会被他的问题难住.”(3)[意大利]恩里卡·克里斯皮诺.达·芬奇[M].田丽娟，张惠，邢延娟，译.南京：译林出版社，2018:12在其他的达·芬奇传记中也有类似的记载(4)欧仁·明茨.列纳奥多·达·芬奇(第一卷)[M].陈立勤，译.北京：人民美术出版社，2014:22..这也说明达·芬奇在16岁之前没有受到良好的数学教育.1468年达·芬奇爷爷去世，16岁的他离开了芬奇镇到意大利文艺复兴中心佛罗伦萨，进入韦罗基奥的画室学习.1473年，达·芬奇完成了自己的第一幅画作——《阿诺河风光》.达·芬奇在韦罗基奥画室工作了8年，24岁离开.1481年到米兰以后，达·芬奇开始接触解剖学、光学、动力学、静力学、地质学、数学等多个学科领域.1494-1495年，绘制《最后的晚餐》，1497年完成.1500年，第二次移居佛罗伦萨时期，达·芬奇对几何学、光学、水学和解剖学进行了深入研究，开展阿尔诺河改道工程，创作《安吉亚里之战》、《岩间圣母》等作品.1513年又去米兰，后又定居罗马，得以潜心于数学、科学和工艺技术的研究，并创作了手稿《几何游戏》.之后开展排水工程工作.1515年，达·芬奇所进行的科学研究被认为是“妖术”，遭到圣灵医院驱逐.1516年绘制《摧毁世界的大洪水》系列图稿.1517年前往法国为国王弗朗索瓦一世服务，进行土地规划研究，并完成了一座巨型城堡的建筑设计工作.此时达·芬奇右手已经瘫痪.1519年5月2日，达·芬奇去世，8月12日，埋葬，骨灰后来遗失.

至于达·芬奇是否为数学家，研究者们有不同看法.1545年“加迪亚诺无名氏”编辑的《莱奥多纳·达·芬奇》中说达·芬奇“精通数学和透视学”(5)[意]莱奥纳多·达·芬奇.绘画论[M].[法]安德烈·夏斯塔尔，编译.邢晓声，译.长沙：湖南美术出版社，2019:34..1550年，乔治·萨瓦里的《莱奥纳多·达·芬奇》中说：达·芬奇“花费数月功夫弄数学，进步神速，甚至经常出难题让老师受窘.”(6)[意]莱奥纳多·达·芬奇.绘画论[M].[法]安德烈·夏斯塔尔，编译.邢晓声，译.长沙：湖南美术出版社，2019:39.美国的麦克·怀特认为达·芬奇是一位不娴熟的勉强及格的数学家(7)麦克·怀特.达芬奇：科学第一人[M].徐琳英，王晶，译.北京：中国人民大学出版社，2011:146.，英国丹尼尔·史密斯认为达·芬奇是“当时杰出的数学家”(8)[英]丹尼尔·史密斯.天才的另一面：达·芬奇[M].肖竞，译.北京：电子工业出版社，2016:133.，有人认为“相比其他学科，列奥纳多在纯粹数学领域的想法较平淡无奇.”(9)欧仁·明茨.列奥纳多·达·芬奇(第二卷)[M].陈立勤，译.北京：人民美术出版社，2014:74.我们根据上述观点和达·芬奇各种手稿中丰富的数学内容，特别是几何作图及其应用以及当时的数学发展水平等因素，认为达·芬奇是一位应用数学家，而且他的数学工作倾向于几何学.

达·芬奇作为数学家，对数学有深刻的理解和认识，并对数学的研究内容的特点、数学价值等方面提出了很多独到见解.他强调：“不是数学家，读不懂我作品中的原理.”(10)[意大利]达·芬奇.达·芬奇艺术与生活随笔[M].戴专，译.北京：光明日报出版社，2012：128.可以换句话说，“不懂数学，勿读吾书.”于是很自然地让人联想到古希腊哲人柏拉图学园匾额上的“不懂几何，不得入内”的千古名言.“不懂数学，勿读吾书”，间接地告诉人们达·芬奇的作品皆以数学原理为基础，因此数学是认识达·芬奇天才智慧的一把钥匙.

2 达·芬奇手稿、笔记和藏书

探寻达·芬奇艺术、科学技术的学习和研究成长道路时，他丰沛的手稿会提供关键信息，丰富的藏书也揭示了他学习研究的广度.因此有必要简要介绍其手稿、笔记和藏书情况.

2.1 达·芬奇手稿

达·芬奇手稿是我们去认识他伟大而辉煌成就的窗口.达·芬奇的手稿可以用“浩如烟海”来形容，多达3万页，所涉及学科领域非常广泛.1519年达·芬奇去世后，其手稿全部由达·芬奇学生弗朗西斯科·梅尔兹继承，一直保存到1570年.遗憾的是梅尔兹的儿子奥拉齐奥对这些手稿毫无兴趣，于是这些手稿遭遇了四散流落的厄运.目前只有五分之一的手稿被保存下来，现藏于意大利、美国、法国、英国和西班牙等国家.达·芬奇手稿完成时间顺序如表1.

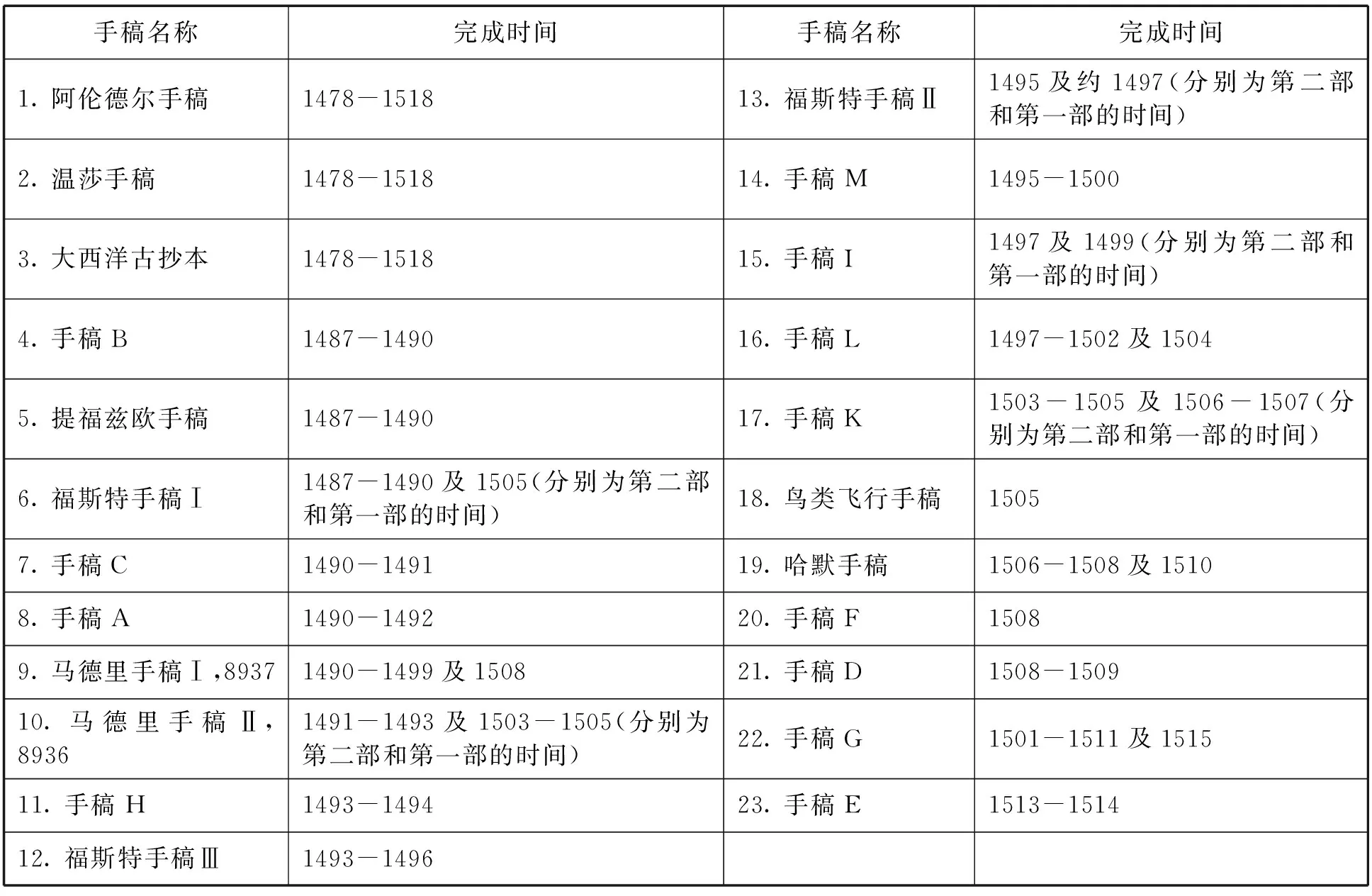
表1 达·芬奇手稿一览表

从目前我们掌握的情况看，在《大西洋古抄本》《马德里手稿》《哈默手稿》《福斯特手稿Ⅰ》《手稿L》等手稿中有数学内容，内容不重复，侧重点不同.其中，《大西洋古抄本》《马德里手稿》中的数学内容最多，因此这里主要以这两本手稿为重点论述达·芬奇的数学工作.

《大西洋古抄本》(11)Leonardo Da Vinci.DISEGNI DI MACHINE ET DELIE ARTI SECRET ET ALTRE COSE DI LEONARDO DA VINCI RACOLTI DA POMPEO LEO NI(1478-1519)[M].Milan,1964.是达·芬奇举世闻名的手稿，自1637年以来保存在安布罗西亚纳图书馆，分12卷，1119页，羚羊皮装订，尺寸为60.5 cm×46.0cm，如图2.莫皮奥·列奥尼巴·达·芬奇将达·芬奇的1750页手稿和零散的碎片粘在大规格纸张上并装订成册.由于大规格纸张像地图册一样大小，因此起名为《大西洋古抄本》.手稿包括武器设计、民用装置、建筑与几何、飞行与运动四个领域，可以分为24个主题，其中数学手稿至少有220页.每一个领域均用到几何学作图知识，但是只有在“建筑与几何”中有几何学研究内容.即编号849v“建筑与几何学研究”、编号762v“建筑设计与几何学研究”、编号696r“圆规和几何设计”、编号471v“几何游戏”、编号505r“用曲线切割方形”、编号307v“从圆到星型结构”、编号518r“几何学研究”等.从整体上看，所谓的几何学研究就是几何作图、几何证明和几何应用，但是达·芬奇没有给出作图步骤，每一幅作品中呈现的几何图形特点各自相异.

图1 达·芬奇肖像

图2 《大西洋古抄本》

《马德里手稿》是达·芬奇两卷手稿的总称，均藏于西班牙马德里国立图书馆，其索引号分别是8937和8936，为第I卷和第II卷，如图3.1966年这两本手稿在西班牙国家图书馆偶然发现.1830年，由于当时两卷手稿被皇家图书馆收入并进行分类编目时出现标识错误，长期以来人们对两卷手稿的存在一无所知.

图3 《马德里手稿》

《马德里手稿I，8937》，184页，尺寸为21cm×15cm.第I卷第一部分内容为各种机械绘图，其中包括各式钟表，第二部分内容则主要是对理论力学的研究和几何学研究.

《马德里手稿II，8936》，157页，尺寸为21cm×15cm.该手稿由两个部分组成，在内容和撰写时间方面两部分手稿都迥然相异.该手稿包括河道设计、透视法、光学、比例理论、几何学等内容.在几何内容中有欧几里得《几何原本》的学习心得、几何概念的界定以及对数学研究对象的分类.在该手稿中立体几何内容较多.

2.2 达·芬奇笔记

达·芬奇笔记并不是我们所想象的那样——整齐井然写出来的内容，而是后人从其手稿的不同段落中甄选并按内容分类而形成的笔记.目前在世界上流传的达·芬奇笔记有多种.我们从他的笔记中可以了解其对艺术、科学技术、数学等方面的思想.我们现在掌握的达·芬奇笔记有以下几种：

(1)Edward MacCurdy.The Notebooks of Leonardo Da Vinci [M]. London ：The Reprint Society London，1954.(该书为两卷本，自1938年初版问世以来在美国和英国等国家多次出版.)

(2)Edward MacCurdy.The Notebooks of Leonardo Da Vinci [M].New York：George Braziller，1958. (该书初版是1939年由Reynal &Hitchcock Incorporated，Inc出版.)

(3)H.Anna Suh.Leonardo’s Notebooks:Writing and Art of the Great Master[M].New York：Black Dog &Leventhal Publishers，2005.

(4)[意]列奥纳多·达·芬奇. 达·芬奇笔记[M].[美]H·安娜·苏，编.刘勇，译.长沙：湖南科学技术出版社，2015.

(5)[意大利]达芬奇.达·芬奇艺术与生活笔记[M].戴专，译.北京：光明日报出版社，2012.

(6)[意]莱奥纳多·达·芬奇. 达·芬奇笔记[M].周莉，译.南京：译林出版社，2018.

(7)[意] 达·芬奇. 达·芬奇笔记[M].杜莉，编译.北京：金城出版社，2011.

(8)[英]艾玛·阿·里斯特. 达·芬奇笔记[M].郑福洁，译.北京：生活·读书·新知三联书店，2007.

从数学的角度看，Edward MacCurdy整理的笔记中有“数学”章，30多页，主要是达·芬奇关于数学思想方法及其价值的论述.这是我们宏观地了解达·芬奇的数学工作和数学观的重要文献，但是微观认识达·芬奇数学工作和数学观方面还是有些欠缺，因为在整理笔记时把相关的几何图形全部忽略了.另外，中译本笔记中关于数学内容很少，甚至翻译时译者把关于数学的内容给精简了.因此，中译本笔记给我们提供的信息非常有限.

2.3 达·芬奇藏书

藏书也会反映一个人的阅读兴趣、研究志向、视野广度和思想深度.我们从达·芬奇的藏书可以窥见这一切.达·芬奇是一位藏书家，在那个年代来说他的藏书量是极其丰富的，有116种图书(12)Leonardo Da Vinci. Tratados Varios De Fortificacion Estatica Y Geometria Escritos En Italiano Ⅱ：Library Number 8936[M].Tokyo: Iwanamisyoten, 1975： 2-4.オレナルド·ダ·ヴぃンチ.マドリッド手稿第Ⅲ巻[M].小野健一，訳.東京：岩波書店，1975：95-110．，涉及的领域有数学、天文历法、医学、生物学、工程、建筑、语言、文学、水力学、圣经、哲学等.在他的藏书中有但丁的《神曲》、克雷森齐的《农事书》、阿尔伯蒂的《论绘画》、阿维森纳的《医典》、博纳蒂的《众星之书》、阿玛迪奥的《建筑之书》、欧几里得的《几何原本》和马尔西利奥的《柏拉图神学》等经典著作.不太了解书籍历史的人也许会认为仅藏有116种图书的人还算什么藏书家.让我们从另一个角度看达·芬奇是否是藏书家.如，在15世纪，剑桥大学图书馆的藏书仅有几百册图书(不是几百种)，而且只涵盖了当时人类知识相当有限的方面，且这些藏书主要是宗教方面的，用以培养出识字的牧师(13)[英]杰克·古迪.文艺复兴——一个还是多个？[M].邓沛东，译.杭州：浙江大学出版社，2017：33..

就达·芬奇所藏数学书而言，包括与他工作有关的重要数学书，具体如下：

1.欧几里得几何学(EUCLIDE IN GEOMETRIA)：Euclides, Elementa geometriae(Erhardus Ratdolt,1482年)、Campanus Novariensis(Leonardus Acha-tes & Gulielmus de Papia, 1491年) (Sim. Bivilaqua,1502年).达·芬奇没有说明版本，它可能是以上三种版本之一.

2.Libro de abbaco che insegna a fare ogni ragione mercantile, Stampato nell’inclita citta di Milano per Jo. Antonio Borgo(没有出版年代)，这可能是木板装订的算术教科书Libro d’abaco da Milano， grande， in asse.

3.La nobel opera de arithmetica. . . compilata per Piero Borgi da Veniesia(威尼西亚版，1484年).

4.Filippo Calandri, Ad nobilem et studiosum Julianum Laurentii Medicem,De aritmethrica opusculum(Lorenzo da Morgiani et Giovanni Thedesco da Magonza，1491-1492年).

5.Abaco, ossia maniera facile per apprender ogni conto(1478年).

6. Paolo Dagomari(1281-1374).Trattato d’abbaco,d’astronomia e di segreti naturalie medicinali.

7.透視法概論(PROSPETTIVA COMUNE)：Joannes Cantuariensis, Prospectiva comunis. . . castigata per Facium Cardanum (Petrus Cornenus，约1480年).

8.历法(CALENDARIO)，Joh. Regiomontanus, Calendarium (有1476年、1478年、1482年等版本).

9.Joh. MuellerEphemerides (天体位置推算历).

10. Luca Pacioli de Borgo, Summa de arithmetica. ..(…，Paganino de Paganini, 1494年)

11.圆的求积法(QUADRATURA DEL CIRCULO).

12.算术小册子(LIBRETTO VECHIO D’ARISSMETRICA).

3 达·芬奇的数学定义观及其渊源

达·芬奇认为数学是一门具有确定性的学科，其概念界定明确，内容分类清晰.他说：“那些对数学至高无上的确定性提出质疑的人，只能让自己陷入困惑之中，他永远无法平息那些由矛盾和诡辩术所导致的无休止的争论.”(14)[意大利]达·芬奇.达·芬奇艺术与生活随笔[M].戴专，译.北京：光明日报出版社，2012：128.数学的确定性是判断是非的基准，学习数学也是提高判断能力的过程.判断力在达·芬奇思想中占有至关重要的位置.他认为“‘首先，学习科学，判断力落后于技艺的人是无能的，判断力超越手艺的人才走在追求完美的道路上.’——没有理论支持的行动，就像没有指南针和船舵的水手.”(15)欧仁·明茨.列奥纳多·达·芬奇(第二卷)[M].陈立勤，译.北京：人民美术出版社，2014：55.

达·芬奇对数学确定性的观点是来自于古希腊的毕达哥拉斯、苏格拉底、柏拉图和亚里士多德等贤者的经典著作.他的数学知识多来自于古希腊数学家欧几里得《几何原本》和意大利数学家卢卡·帕乔利的Summa de Arithmetica，Geometria，Proportioni et Proportionalita(《算术、几何、比及比例概要》，1494年).他继承了古希腊数学之“四艺”说，将数学分成算术、几何、天文学和音乐.达·芬奇认为，算术处理的是不连续的量，几何处理的是连续的量.算术是一门计算科学，它有真实和精确的数字，但是对于处理连续量却无济于事.(16)[美]沃尔特·艾萨克森.列奥纳多·达·芬奇传[M].汪冰，译.北京：中信出版社，2018:202.在他的《马德里手稿》中进一步论述时除了连续与不连续之外还有有理量和无理量的概念(17)Leonardo Da Vinci. Tratados Varios De Fortificacion Estatica Y Geometria Escritos En Italiano Ⅱ：Library Number 8936[M].Tokyo: Iwanamisyoten, 1975：46.：算术的研究对象是离散的有理量，几何的研究对象是连续的量，这种量包括无理量和有理量；天文学的研究对象是连续而变化的量；音乐的研究对象是连续的量.达·芬奇对音乐概念的界定与毕达哥拉斯“四艺”中的界定有所不同，毕达哥拉斯认为音乐是研究连续但偶尔离散的量的科学.达·芬奇进而介绍了算术比例、几何比例、调和比例以及不连续比例和连续比例的概念.这些数学知识的获得来自于他的数学启蒙老师卢卡·帕乔利的著作.

达·芬奇的数学研究主要依靠他的超凡的空间直觉能力，详细的论证并不多，但是他非常注重数学概念的定义，而且极为详细.如，他对点、线、面、角、正方形、长方形、菱形、平行线、圆及其直径和半径、直线形中的三角形及其种类、四边形和多边形(18)レオナルド·ダ·ヴィンチ.マドリッド手稿Ⅴ[M].東京：岩波書店，1975：295-298.、曲线中的弓形、月牙形、镰刀形和叶子形等概念给出了详细的定义.

达·芬奇定义如下图4(19)Leonardo Da Vinci. Tratados Varios De Fortificacion Estatica Y Geometria Escritos En Italiano Ⅱ：Library Number 8936[M].Tokyo: Iwanamisyoten, 1975：140.，阐明了正方形、长方形、平行四边形、菱形、圆、半圆及直径、弓形、三角形及其种类.

图4 达·芬奇定义几何图形概念

这里有必要简要介绍达·芬奇的弓形定义.笔者在查阅大量与达·芬奇数学手稿有关的历史文献时发现，国内出版的不少数学工具书、数学史书、中译本的达芬奇传记和少量的达·芬奇手稿中将月牙形称为弓形，造成对弓形、月牙形等概念认识的混乱.事实上，达·芬奇严格区分了弓形、月牙形、镰刀形和叶子形四个概念.因为这四个图形在达·芬奇的整个创造工作中提供了不可替代的基本的工具性素材.如果达·芬奇离开了这四个几何图形，那么他的多数创造性设计就不会存在，换言之多数手稿也就不可能出现了.

弓形：所谓圆的弓形是不等于圆直径的线段将该圆分割两部分所形成的两个几何图形.(如果该线段等于直径，则将圆分成两个相同的部分，即半圆.)如图5(20)レオナルド·ダ·ヴィンチ.マドリッド手稿Ⅴ[M].東京：岩波書店，1975：139..

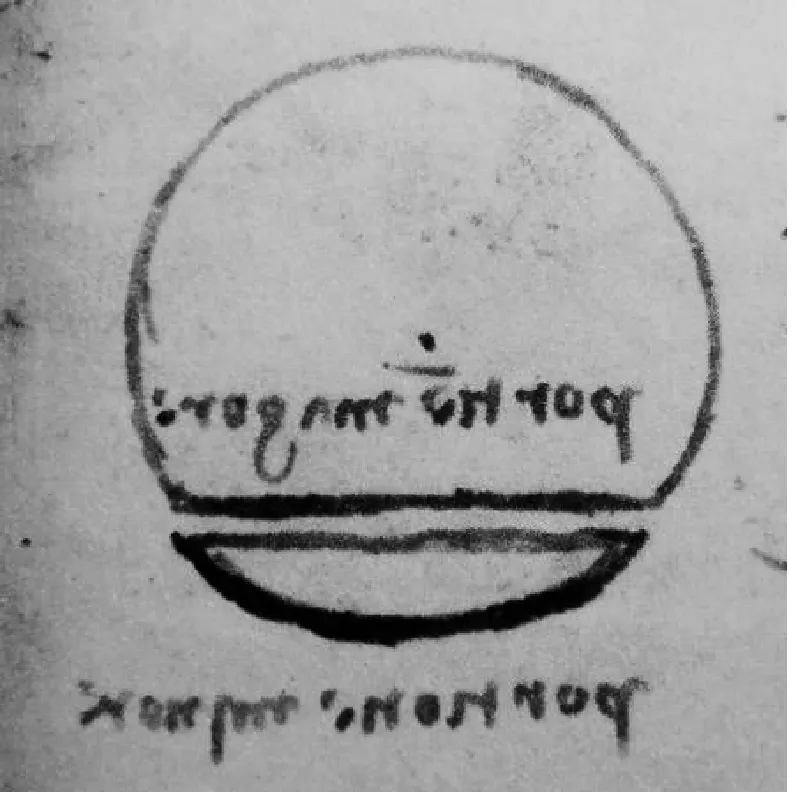
图5 弓形

月牙形：在直角三角形中，如果以两直角边为直径向形外作半圆，又以斜边为直径向形内作半圆，则斜边上的圆和两个直角边上圆相交所形成的非阴影图形叫做月牙形.直角三角形面积等于两个月牙形面积之和.如图6(21)达·芬奇.大西洋古抄本[M].第1563页.，图中的阴影部分就是弓形.

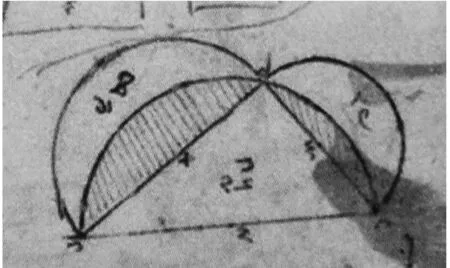
图6 月牙形

镰刀形：在一条线段上依次向左(或向右)作半圆，这些半圆直径的一个端点(右侧)是共同的，其他半圆直径的端点依次相隔等距离而成的图形，如图7(22)达·芬奇.大西洋古抄本[M].第1803页..关于镰刀形的研究并不是达·芬奇开创的，早在古希腊罗马时期已经有了，在那时用镰刀形所形成的圆的直径上被分割的线段长度关系表示音程(23)[古罗马]维特鲁威.建筑十书(典藏版)[M].[美]I.D.罗兰，英译，[美]T.N.豪，评注；陈平，中译.北京：北京大学出版社，2019:241..

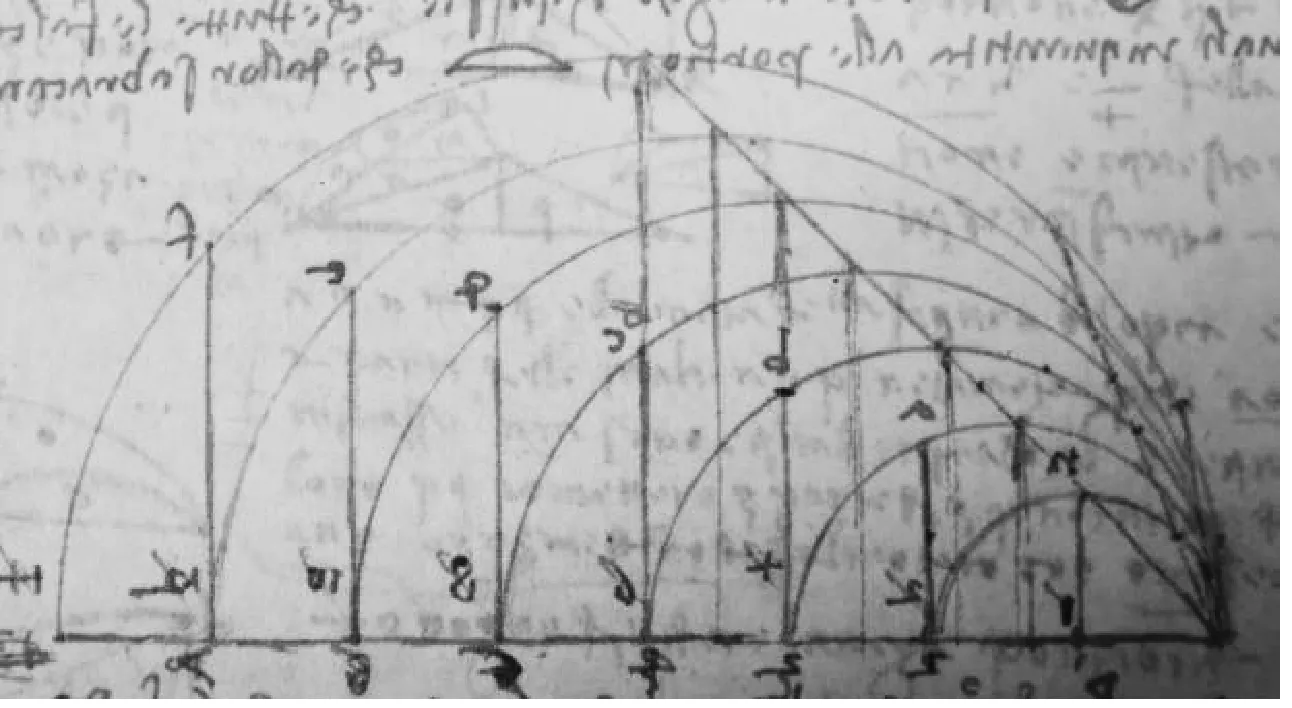
图7 镰刀形

叶子形：两个圆相交之后形成的公共部分，如图8(24)达·芬奇.大西洋古抄本[M].第1229页..叶子形是在达·芬奇手稿中出现最多的一种.

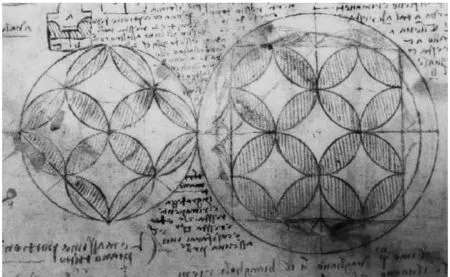
图8 叶子形

达·芬奇对概念下定义，在揭示概念内涵时以追究知识终极起源的哲学思想为基础的，他说(25)[意大利]达·芬奇.达·芬奇艺术与生活笔记[M]. 戴专，译.北京：光明日报出版社，2012：129-130.：

科学是大脑对事物终极起源原理的研究，除了终极起源，大自然没有其他的物质能够组成事物的各个部分.举例来说，在连续量中，也即几何学中，先是从物体的各个面开始，面的起始与终止都是线；我们不能满足于此，因为我们知道线终结于点，而点是最小的单位.因此点就成了几何学的第一起源，不论是在自然还是在人的头脑中，都没有什么能让点再次被分割了.如果你说，当一个平面与铁器的尖头发生接触后就创造了点，那是不正确的；我们只能说那个接触点是围绕着它的中心形成的面，而中心才是点.这个点并不是构成面的一部分，无论是它还是世界上所有的点，哪怕它们都组合起来——假设它们能组合起来——也无法构成这个面的任何一部分.你可以想象，假设一个完整的平面由一千个点构成，如果我们将这一平面分成一千份，我们仍然能说，分开后的每一部分其包含的点跟未分之前的平面，其点的数量是一样的；我们可以用无，也就是十进位算术中的零，来证明它.零代表着什么也没有，但将它放在其他数字后面，就会成为那一数字的十倍， 如果那一数字后面有两个零， 则是一百倍.每往数字后增加一个零，新的数字就是未加零之前那个数字的十倍，如此反复，可让数字到无穷大.但零本身就是无，全世界所有的零加起来，跟一个零在内容和价值上都是相同的.

这里对几何学中点的论述是颇为精彩的，认为点是没有大小只有位置的一个存在.他担心别人可能不易理解他的解释，进而将点、无、零这三个要素结合起来阐释.这实际上局部地揭示了几何学和算术之间的内在联系，体现了数形结合的思想方法.达·芬奇的这番阐释让人们联想到德国哲学家黑格尔，特别是恩格斯对零的解释.比达·芬奇晚300多年的恩格斯认为(26)恩格斯.自然辩证法[M].中共中央马克思恩格斯列宁斯大林著作编译局，译.北京：人民出版社，2018:191-192.：

零是任何一个确定的量的否定，所以不是没有内容的.相反，零具有非常确定的内容.作为一切正数和负数之间的界限，作为既不是正又不是负的唯一的真正的中性数，零不只是一个非常确定的数，而且它本身比其他一切以它为界限的数都更重要.事实上，零比其他任何一个数都有更丰富的内容.把它放在其他任何一个数的右边，按我们的记数法它就使该数变成原来的十倍.在这里，本来也可以用其他任何一个记号来表示零，但是有一条件，即这个记号就其本身来说表示零，即等于0.因此，零本身的性质决定了零有这样的用处，而且唯有它才能够这样应用.

在如何理解零的问题上，达·芬奇和恩格斯的观点基本相同，不同之处在于达·芬奇将零作为终极起源来看待的，恩格斯基于黑格尔的辩证法观点阐释了零.

另外，达·芬奇说：“如果我们将这一平面分成一千份，我们仍然能说，分开后的每一部分其包含的点跟未分之前的平面，其点的数量是一样的.”这段论述表明在平面任何一个小块上点数和原来平面的点数相等.达·芬奇的该结论让人们立即联想到实变函数中的相关理论，即实数轴上任何一个区间与实数集对等，即任何一个区间的基数与实数集的基数相等，它们都是阿列夫(连续基数或连续统势c)，同理，平面上任何一个小块和整个平面也具有相同的基数.

4 达·芬奇求面积及其思想内涵

达·芬奇的数学学习和研究的重点在于几何作图，但是作图并不是单纯的几何图案和各种设计中的作图，更不是简单的作图案.

这里主要介绍达·芬奇求三角形和圆面积的对称性“割补法”和等积变换法.在达·芬奇手稿中多处见到求三角形面积、圆面积和正方形加倍问题的图形.因此，在此主要以“762v建筑设计与几何学研究”为例论述，同时相应地阐述有关问题的历史渊源.

4.1 三角形面积

“建筑设计与几何学研究”中有26幅几何图形，可以分为四类：第一类为正方形内切圆，内切圆的内接正方形，依次做下去.并在圆和正方形之间所产生的同类几何图形中做阴影，形成有规则的建筑设计图案——弓形或叶子形.第二类为作圆内接正方形，并以第一类图形做法进行下去.第三类为现在小学数学教科书中的简单的等积变换的几何图形，即求三角形面积公式的“割补法”，如图10.图10是从图9中截取的.第四类为其他各种复杂的图形，这里不进行讨论.另一个几何图形就是“建筑设计与几何学研究”中间的正方形内接正方形(27)达·芬奇.大西洋古抄本[M].第786页..

图9 建筑设计与几何学研究

图10 三角形面积

由图9可以截取图10后可见，如果是直角三角形，则将直角三角形中位线上方小三角形旋转180°，直角三角形变成矩形，即矩形面积就是直角三角形面积.如果不是直角三角形，则作三角形高与中位线，将中位线上方两个小直角三角形旋转180°，使三角形变成矩形.矩形的面积就是三角形的面积.另外，从第二个三角形图也可以看到，以三角形高将原来三角形分成两个直角三角形，则分别以两个直角三角形斜边的中点为中心将两个直角三角形相反方向旋转180°，则得到的矩形面积等于原三角形面积的两倍.综上所述，达·芬奇实际上给出了求三角形面积的三种方法.

《马德里手稿》中也讨论了三角形面积和锥体体积.达·芬奇说：“任意三角形的面积是其底边与高的乘积的二分之一.任意锥体的体积是底面与其高的乘积的三分之一.”如图11(28)Leonardo Da Vinci. Tratados Varios De Fortificacion Estatica Y Geometria Escritos En Italiano Ⅱ：Library Number 8936[M].Tokyo: Iwanamisyoten, 1975：70..从图形看，三角形面积的表达直观清晰，但是锥体的体积的图形表达显得拙劣一些.

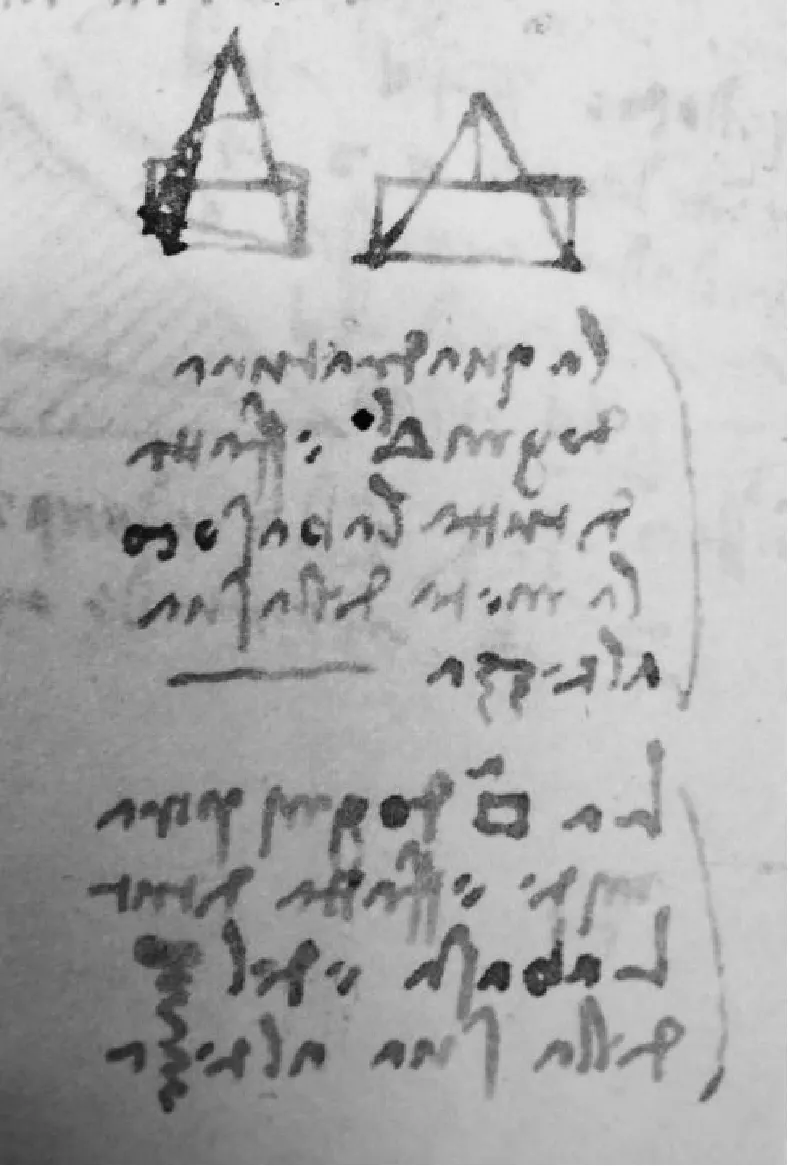
图11 《马德里手稿》中的三角形

这一方法与中国南宋数学家和数学教育家杨辉(字谦光，约13世纪中叶至后半叶活动于苏、杭一带)求三角形面积方法不谋而合.杨辉在《田亩比类乘除捷法》中用刘徽的“以盈补虚”方法来详细地阐明了三角形面积公式的推导，补充了各种可能的情况，使得推理方法更严谨、灵活.具体如下：

“广步可以折半者，用半广以乘正从.从步可以折半者，用半从步以乘广.广从皆不可折半者，用广从相乘折半.”

用几何图形表示如图12(已知△ABC，D、E分别为边AB、AC的中点).

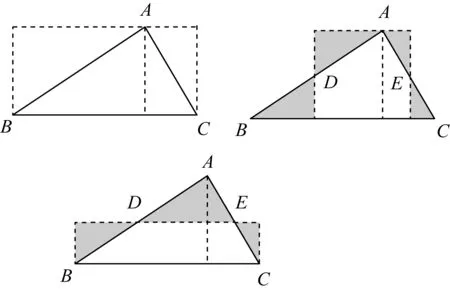
图12 杨辉求三角形面积法

4.2 圆面积

求圆面积是现在小学数学中常识性知识，但也是重要内容之一，因为它蕴含着深刻的数学思想方法——将曲线形变成直线形的辩证思想方法.西方数学教育史告诉我们，达·芬奇那个年代还没有像现在这样系统的学校数学教科书，虽然《几何原本》是公认的教科书，但是对一般的学习者来讲读懂它并不是一件容易的事情.达·芬奇对初等几何的兴趣浓厚而广泛，他热衷于圆面积的求法，在其手稿中也有不少相关内容.如图13(29)达·芬奇.大西洋古抄本[M].第1203页.所示，在图的左下角的将圆分割成若干个相等部分，并将它转化为平行四边形.这是我们所熟悉的求圆面积的方法.达·芬奇形象地描述圆面积，即圆如车轮，圆的半径相当于车条，假如车轮有16个车条，那么它们把车轮分成16个全等的扇形(看作小等腰三角形)，用16个等腰三角形可以制作一个平行四边形，于是圆面积可看作为平行四边形的面积.

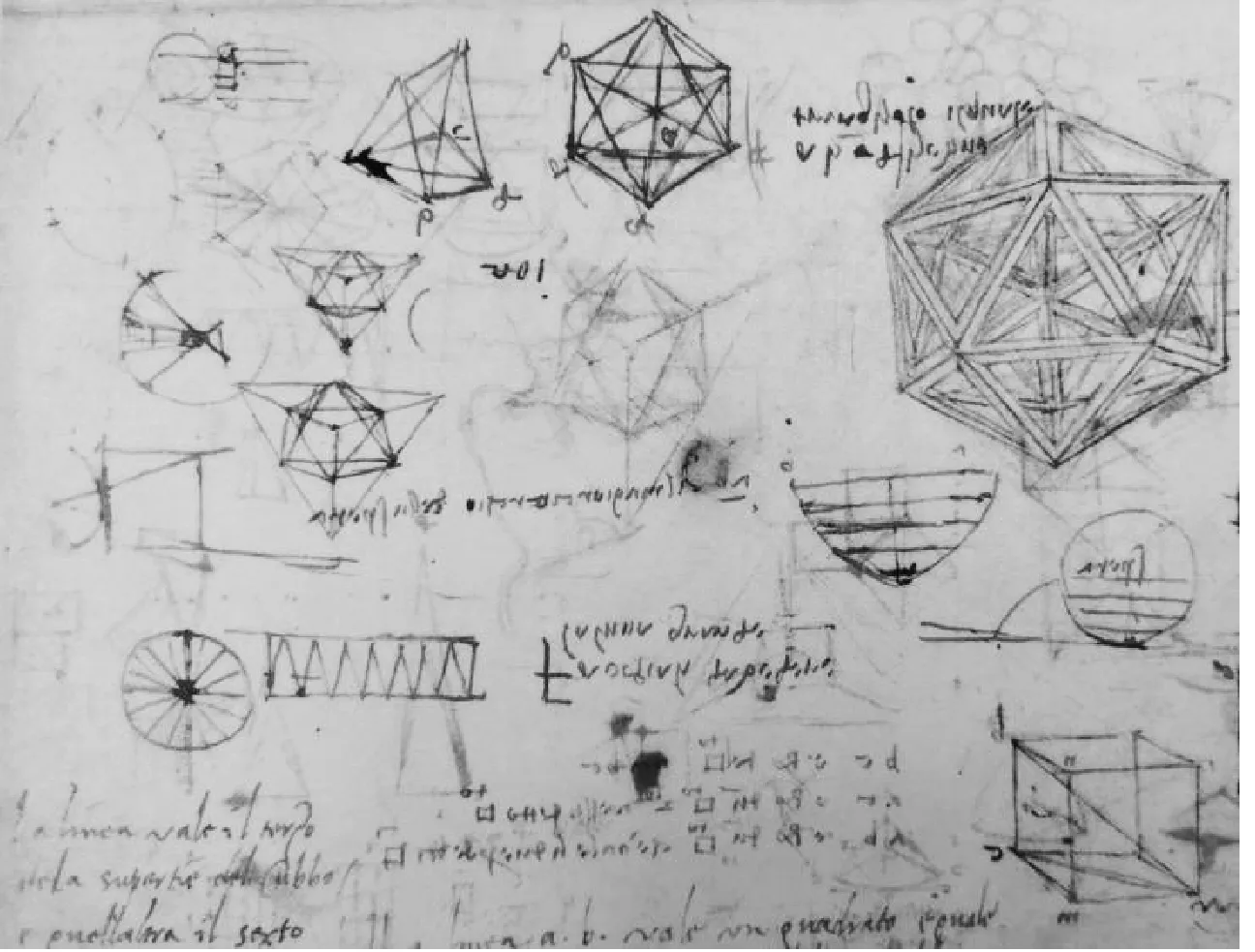
图13 圆面积与多面体

4.3 正方形面积加倍问题

正方形面积加倍或者用已知正方形制作其两倍面积的正方形的问题已有两千多年的历史，它也是勾股定理的特殊情形.这一问题也自然地成为达·芬奇研究的主题之一，在他的手稿中多处可以看到这一问题的各种直观表示.如编号为849v“建筑与几何学研究”局部中，有3个正方形面积加倍的几何图形，如图14.又如，编号为762v“建筑设计与几何学研究”中部有微小的正方形面积加倍的几何图形，放大后如图15.

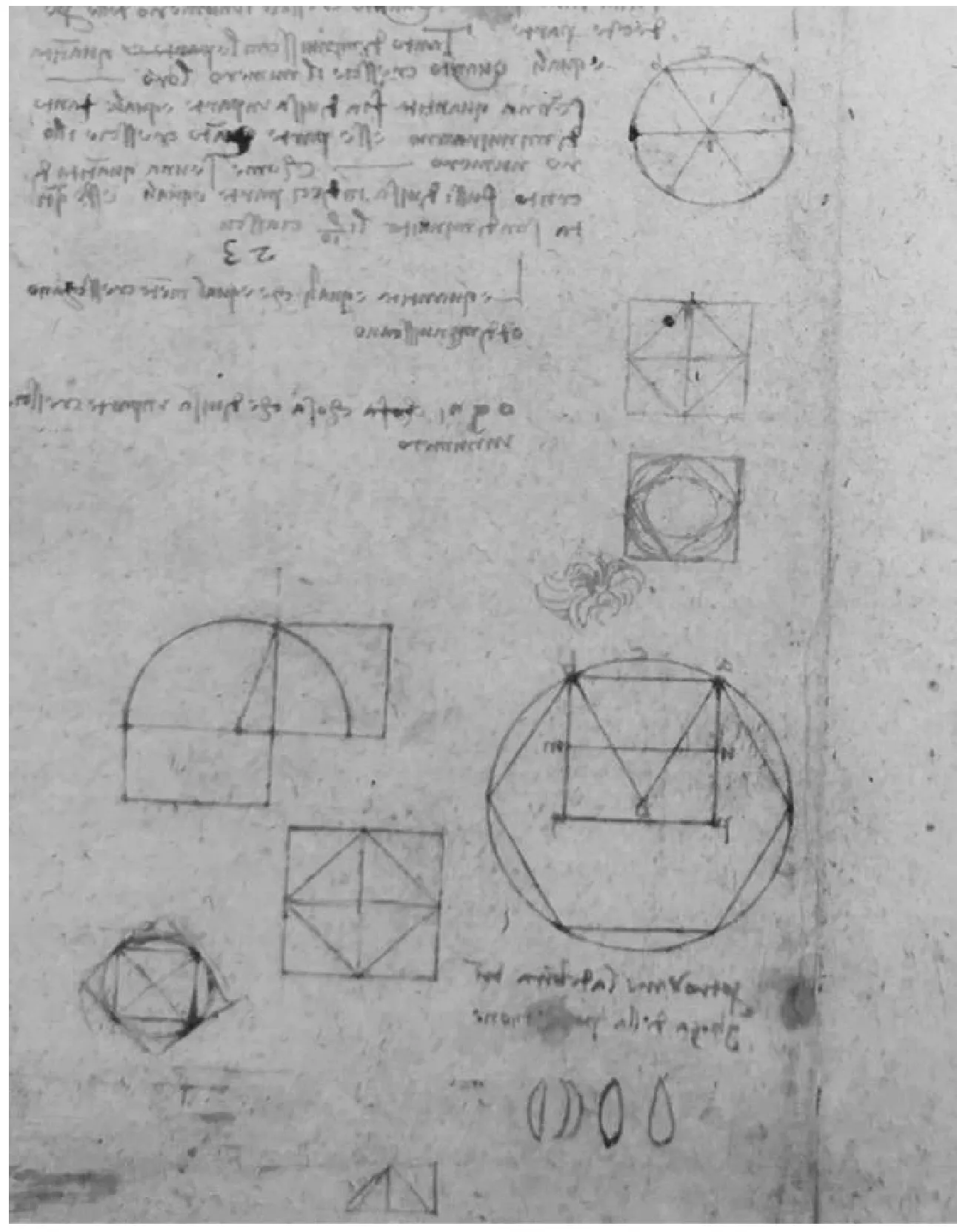
图14 编号849v“建筑与几何学研究”局部

图15 762v“建筑设计与几何学研究”局部

达·芬奇的正方形面积加倍问题的几何图形看似很简单，但是它让人们浮想联翩，引领人们在数学的历史长河中漫游.

首先，这个问题让达·芬奇本人也感到沮丧，因为边长为有理数的正方形的对角线是无法用他的直观理解表达出来的.“在正方形的正下方，达·芬奇用一行小字克制地表达了他当时沮丧的心情：‘如果我做成过什么事，请告诉我吧.’这句话在他的手稿中曾以不同的缩写形式出现过很多次.数学的神秘感和无穷无尽的谜题，常常令他感到沮丧.”(30)[英]马丁·肯普.达·芬奇100个里程碑[M].叶芙蓉，译.北京：金城出版社，2019:85.

其次，让人们联想到苏格拉底回忆知识的故事(柏拉图《美诺篇》)，苏格拉底用“产婆术”使一个奴隶小孩回忆起——制作已知正方形的两倍面积的正方形，即用两个相同的正方形制作一个正方形.不妨把这个问题简称“苏格拉底问题”.另一方面，该图形让人联想到勾股定理的特殊情形，即等腰直角三角形的斜边上正方形面积等于两个直角边上的正方形的面积之和.“苏格拉底问题”也引发更具有挑战意义的扩展问题：用两个不同的正方形能否制作一个新的正方形？用n个正方形能否制作一个正方形？

在维特鲁威的《建筑十书》中也有该故事的改编版，给正方形赋予了具体数字，具体如下(31)[古罗马]维特鲁威.建筑十书(典藏版)[M].[美]I.D.罗兰，英译，[美]T.N.豪，评注；陈平，中译.北京：北京大学出版社，2019:190.：

首先，我将举例柏拉图众多极其实用的发现之一，正如他所说明的.有一块正方形的基址或田地，各边长度相等，如果要它的面积成为原来的两倍，就需要一种数字，这种数字通过计算是求不出的，只有画出精准的线条才能求出.以下便是对这个问题的证明：有一块正方形的土地，十足长十足宽，面积一百平方足.如果需要使它的面积翻倍，成为一块二百平方足的土地，同时保持各边同长，那么这正方形的边长应该是多少.通过计算不可能求出此数的，因为如果边长定为十四，那么将边长相乘便得出196平方足；如果边长为十五，会得出225平方足.因此，答案靠数字是求不出的.

这里的所谓算不出来的数字，就是不可通约量，即为无理数.从维特鲁威的这段所谓的证明容易知道，柏拉图的《美诺篇》中的故事为西方古代建筑理论家提供了一个重要启示——有些数学问题不用计算而用几何知识就可以得出不同对象之间的数量关系.

最后，西方哲学家借助“苏格拉底问题”阐述自己的数学教育观点.如德国著名哲学家叔本华也曾经讨论该问题.叔本华提出(32)[德]叔本华.作为意志和表象的世界[M].石冲白，译.北京：商务印书馆，2018:114—119.：

欧几里得所证明的一切如此如彼，都是人们为矛盾律所迫不得不承认的，但是何以如此如彼，那就无法得知了.所以人们几乎是好像看过魔术表演一样，有一种不太舒服的感受；事实上，欧几里得大多数的证明都显著地像魔术.

通常在几何学中，例如在毕达哥拉斯定理中，需要作出一些直线，却不明白为什么要这样做；往后才发现这些原来都是圈套，出其不意地收紧这圈套的口，就俘虏了学习人的信服，学习人只得拜倒而承认一些他完全不懂个中情况的东西.事实竟至于此，学习人可以从头至尾研读欧几里得的著作，然而仍不能对空间关系的规律有任何真正的理解；代之而有的只是背诵一些来自此等规律的结果.这种原属经验的，非科学的知识就如一个医生，他虽知道什么病要用什么药，却不认识两者间的关系一样.

毕达哥拉斯定理也告诉了我们直角三角形的一种隐秘属性.(如图16)欧几里得那矫揉造作，挖空心思的证明，一到“何以如此”就避而不见面了；而下列简单的，已经熟知的图形，一眼看去，就比他那个证明强得多.这图形让我们有透入这事的理解，使我们从内心坚定地理解[上述]那种必然性，理解[上述]那种属性对于直角的依赖性；在勾股两边不相等的时候，要解决问题当然也可以从直观理解入手.

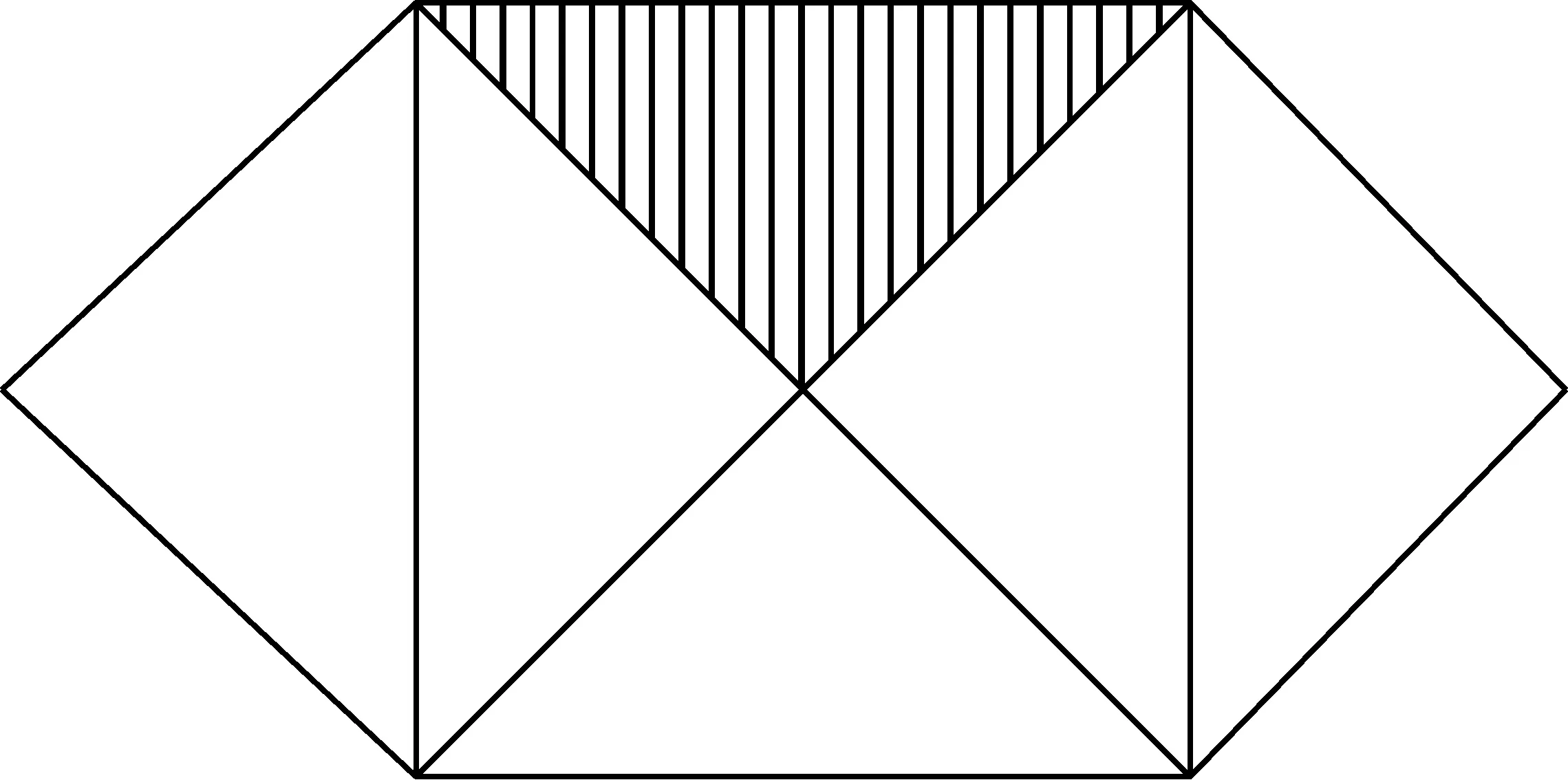
图16 毕达哥拉斯定理的特例

罗素借助苏格拉底的回忆说时也讨论过该问题(33)[英]伯兰特·罗素.西方的智慧——从社会政治背景对西方哲学所作的历史考察[M].温锡增，译.北京：商务印书馆，1999:69..(未完待续)