形涵并重，自然建构规律

■江苏省江阴市晨光实验小学 蒋新娅

一、解读剖析，寻根究因

乘法分配律到底难在哪里？学生出错的原因是什么？数学教师以前在教学中存在什么共同问题？笔者反复研读教材，查阅了相关资料，也对学生进行了访谈调查，与备课组的教师商讨分析，有了以下一些思考。

（一）结构复杂

学生以前学过的运算律都只涉及一种运算，等号两边都只有一种运算，结构简单，等号两边数的个数都不变。而乘法分配律等号两边数的个数、运算符号及运算顺序也不完全一样。如此复杂的结构特征，学生理解、记忆和运用的难度增加了。

（二）表述抽象

乘法交换律和乘法结合律直观形象，学生比较容易用语言归纳表达。而教材中乘法分配律是这样表述的：两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再把所得的积相加，这叫作乘法分配律。这样的定义对学生来说太长、太过抽象，阅读、理解记忆起来很有负担。

（三）负面迁移

前面学过的其他运算律对于乘法分配律的学习，虽然研究方法有一定的正迁移，但也会造成一定的负迁移。学生特别会将乘法分配律与乘法结合律混淆，在运用它们时经常会张冠李戴。

（四）变式多样

应用乘法交换律和乘法结合律简便计算时，等式的两边只是交换乘数的位置或者改变运算顺序，模式比较固定。而应用乘法分配律简便计算的题型多样，有分配形式的顺向应用，也有合成形式的逆向应用，还有其他形式的变式应用。学生既要关注算式中的数据特征，还要思考怎样运用乘法分配律灵活地拆分、合并数据等，使计算简便且结果不变，这对学生来说难度相当大。

二、实践尝试，探求良策

（一）联系生活情境，抽象等式

数学教师要设法挖掘生活素材，使学生在具体生动的情境中形象地理解所学知识，感受和体验数学知识形成的过程。教学中笔者创设了这样两个情境：

①农庄里有樱桃树7行，每行12棵；有杏树3行，每行12棵。果园里的樱桃树和杏树一共多少棵？

②一张桌子56元，一把椅子24元，15套这样的桌椅一共要多少元？

果树、桌椅都是学生熟悉的生活事物，他们根据题意列出了两种不同的综合算式解答。不同的算式求的是同一个问题，因此可以自然地抽象得出两个等式。这样的学习是生动的，学生真正体会到了数学与生活的联系，感受到数学的应用价值。

（二）采用数形结合，直观解释

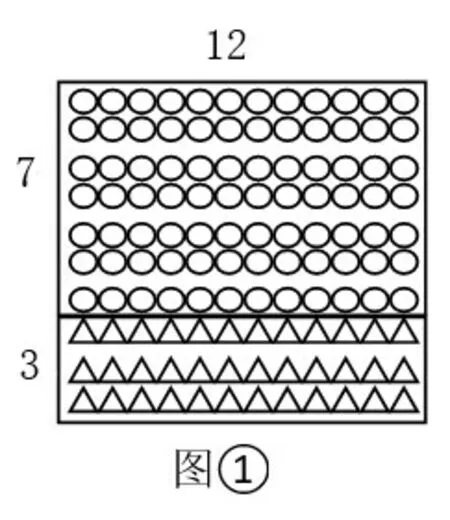
数形结合，可以使抽象的数学语言、数量关系变得具体形象，便于理解。笔者引导学生根据题意画出了如下两个示意图，从而理解等式左右两边不同算式的具体意义。

如图①所示，算式7×12＋3×12是分别算出樱桃树和杏树各有多少棵，再相加；因为樱桃树和杏树每行都是12棵，也可以先算樱桃树和杏树一共有几行，再乘每行12棵，算式是（7+3）×12。不管哪种方法，都是求两种树的总棵数，所以7×12＋3×12=（7+3）×12。

如图②所示，横着看，算式56×15＋24×15是先分别算出15张桌子和15把椅子的价钱，再相加；也可以竖着看示意图，先求出一套桌椅的价钱，再算15套的总价，算式是（56+24）×15。不管哪种方法，都是求15套桌椅的总价钱，所以56×15＋24×15=（56+24）×15。

算式与图形结合，丰富了学生的表象，也更加直观地解释了等式左右两边在形式上不同的本质原因。

（三）挖掘算式意义，理解内涵

在教学中，教师还应该引导学生脱离情境，对学习素材进行数学化的思考，从算式意义上究其本质。

笔者进一步引导学生从乘法的意义来理解等式的含义。如：7×12＋3×12=（7+3）×12，左边表示7个12加上3个12，也就是10个12，右边也表示10个12，所以相等。56×15＋24×15=（56+24）×15，左边表示56个15加上24个15，就是80个15，右边也表示80个15，所以相等。清晰的数学表象在学生的头脑中建立起来，他们透过表象挖掘规律的内涵，真正理解了等式两边结构变化与运算意义的密切联系。

（四）创编生活实例，丰富感知

情境不仅能抽象出等式，也是学生理解和思考的依托。教学中，教师应该将情境用好、用实，为数学学习提供有力的支撑。在上述两个情境的基础上，笔者进一步引导学生思考：如果调整梨树、杏树的行数和每行棵数（每行棵树要相等），桌椅的套数和单价（桌椅数量要相等），是否又能得出一些类似的等式？你能试着再创编出其他生活问题来解释等式吗？学生思维被启发，感知从单一到丰富，自然而然地明白：不管是这两个情境还是自己创编的例子，相关数据改变，还是能够得到类似等式。根据这些丰富的等式，学生自然有了猜想，再举例验证，最后归纳概括得出规律，学生头脑中一步步自然建构出了乘法分配律的模型。

（五）设计对比辨析，厘清本质

在简便计算时，学生将乘法分配律与乘法结合律混淆的错误频频发生，这说明学生只是单纯地机械记忆和模仿，没有厘清两个规律的本质区别。

针对这一现象，笔者设计了几个层次的对比辨析活动。第一个层次：引导学生对比乘法分配律和乘法结合律的字母表达式，比较它们有什么相同和不同？第二个层次：简便计算25×44，要求用不同方法，并比较两种方法的不同。25×44=25×4×11=100×11=1100；25×44=25×（40＋4）=25×40＋25×4=1000＋100=1100。学生通过对比分析，发现要根据算式特点决定用哪种运算律。三个数连乘，应该运用乘法结合律；算式中是两种运算，两个数的和乘第三个数，可以运用乘法分配律。通过这样的对比辨析，学生深刻理解并区分出了这两种运算律的本质区别，运用它们简便计算时就会更加自如。

总而言之，所有的教学研究都应该落实到具体的教学实践中，从而发现问题、解决问题。乘法分配律的教学，一定要聚焦数学的本质，引导学生经历规律的建构过程，从多个方面理解规律的外形结构与本质内涵，从而完善认知结构，感悟数学思想方法，提升数学学习能力。