基于改进粒子群人工鱼群算法的二维熵多阈值快速图像分割

伍蓥芮，张志勇

（山西农业大学农业工程学院，晋中030801）

0 引言

图像分割方法多种多样，其中阈值分割基于背景与目标在灰度上的差异实现图像分割。图像复杂或背景多样时需要选择多个阈值。多阈值分割与单阈值分割原理相似但计算量呈指数级增长，且多阈值分割应用范围更广。

常用的图像阈值分割方法，如大津算法（OTSU）、峰谷法和图像最大熵法等，都是根据图像的局部或全局信息来定位最佳阈值，步骤繁琐导致运算时间较长。为了加快阈值选择速度，程万胜等人[1]运用修正惯性因子的粒子群优化算法提升收敛速率，改善图像在线分割速度；何志勇等人[2]提出基于图像二维直方图直线分割思想的新算法，一定程度上避免传统算法的抗噪缺陷；张怀柱等人[3]提出以二维Fisher准则图像分割评价函数为适应度函数的改进遗传算法，该算法收敛快、鲁棒性强，具有一定实用性。由于信息熵本身能简单有效地表达图像的混乱程度，常将图像熵应用于图像分割。文献[4-5]提出利用图像二维熵来表达基于图像理论信息准则的背景与目标，便于两者分割，该方法仍存在耗时长的问题。文献[6]使用改进粒子群算法结合图像分割与其他算法对比，在不同指标下性能更好。文献[7]和文献[9]提出使用遗传算法（Genetic Algo⁃rithm，GA）来确定图像熵函数的最优值，但遗传算法的变异因子不便控制会影响熵函数的阈值精度。Ming-Huwi Horng[8]使用蜜蜂交配优化算法寻找基于最小交叉熵下的最优阈值。文献[10-11]使用萤火虫算法来选择阈值，该算法更接近穷举算法的结果，且时效性有一定的提升。上述方法都提升了阈值定位的收敛速度，但萤火虫算法、PSO算法与GA算法等智能算法都易陷入早熟无法自动跳出，不能有效拓展搜索范围，导致阈值挑选准确性不高进而影响图像分割效果。

人工鱼群算法（Artificial Fish Swarm Algorithm，AFSA）和粒子群算法都是群体智能仿生算法，AFSA对优化函数的性质要求不高，全局寻优能力灵活，一定程度上避免局部最优点；PSO是模仿鸟类觅食行为的仿生算法，不依赖问题信息，算法通用性较强，但局部搜索能力较差，搜索精度待提高，整体搜索性能对初始参数有一定的依赖性。文献[12]参考PSO的进化策略与信息策略得到一种改进的人工鱼群算法，并在理论上证明PSO-AFSA的收敛性。文献[13]利用高铁数据仿真验证了人工鱼群算法在列车运行调整中的收敛性与实用性，具有一定的应用价值。文献[14]引入方向算子改进的人工鱼群算法以减少局部极值出现的概率。

由于粒子群人工鱼群算法的搜索范围广和局部收敛快的优点和二维熵多阈值分割法的简单实用与分割效果良好，本文设定二维熵多阈值函数为粒子群人工鱼群混合算法的优化目标，基于图像熵对复杂图像和多目标进行分割。

1 基于改进算法的二维熵多阈值图像分割方法

1.1 二维熵多阈值分割原理

设原始灰度图像I(x,y)大小为M*N，M、N为图像横纵像素数，图像灰度级数为L（一般为255）。则可定义该图像每个像素点所对应n*n领域的平均灰度：

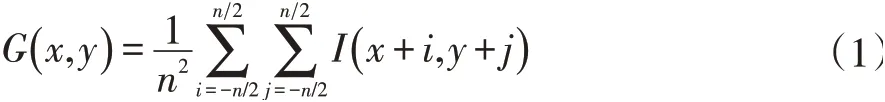
位于图像边缘的像素点，其领域像素点值与中心像素点相同。再设Rij为单个像素灰度值i与邻域某个灰度值出现的对应频数，可定义该像素点的联合概率密度为：

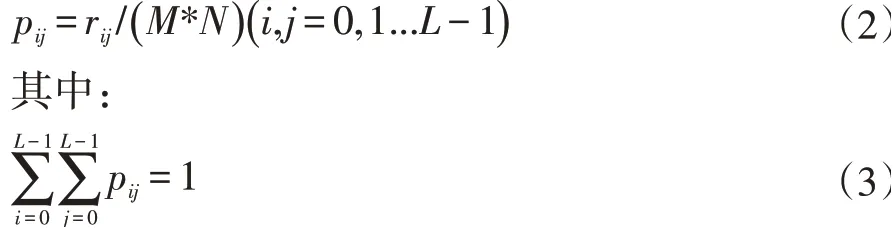
全部像素点Pij可构成原始图像的二维熵直方分布图，图1、图2分别表示单阈值与多阈值直方图。

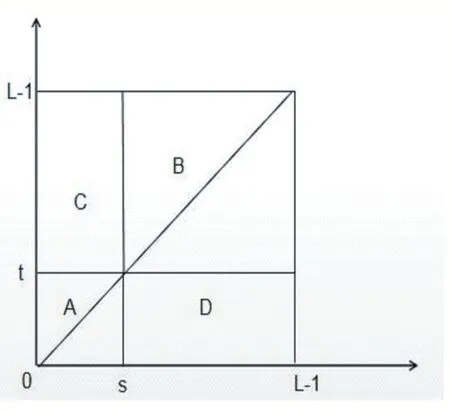
图1 二维直方图

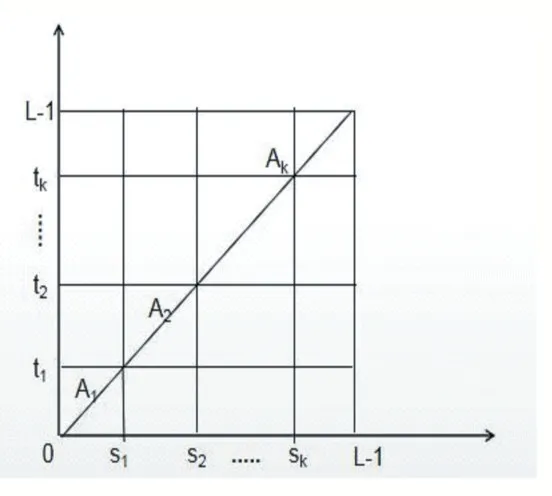
图2 二维多阈值直方图

图1 中，A区代表原图像背景，B区代表目标，C区表示背景与目标相切的边缘，D区表示图像中的噪声；图2与图1类似。A区和B区的灰度像素分布概率分别为：

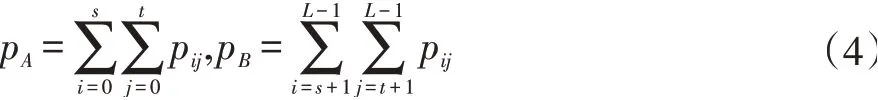
A区与B区域归一化概率为：

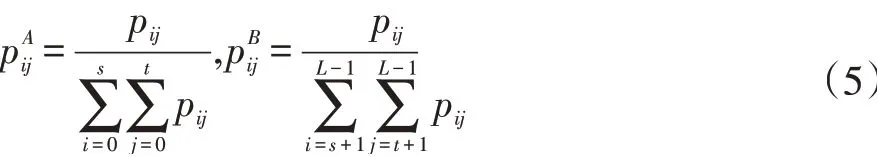
单阈值函数与多阈值函数二维熵分别如下式：

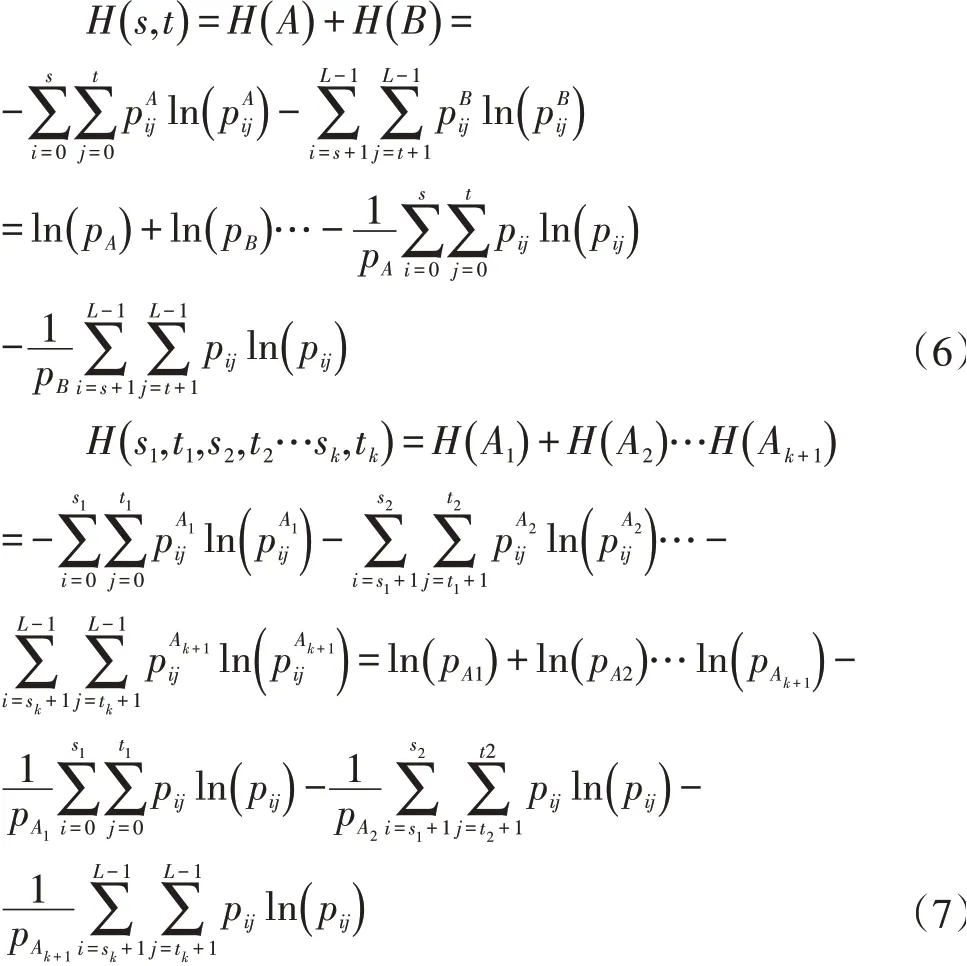
二维熵多阈值图像分割法的分割目标为求阈值（s1，t1）…（sk，tk）使得二维熵函数值为最大。

1.2 粒子群人工鱼群算法

（1）PSO原理

粒子群算法（PSO）是一种仿生优化算法，最初是模仿鸟类觅食运动来寻找适应度函数的极值。鸟类在一定范围内觅食过程中，能不断通过协同交流来寻找食物的位置并分享自己的位置，且每只鸟都有单独记忆。通过这种合作方式，能够将位置信息与食物信息传递至整个群体，提高了整体觅食的效率。在设定为D维的空间中有n只鸟组成的鸟群，在第k次迭代后，其中第i个粒子对应状态为：

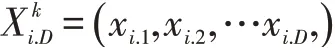
第i个粒子速度为：

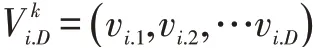
第i个粒子历史最优值：

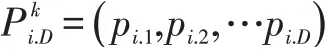
群体中最优点：

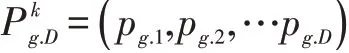
第k+1次迭代的粒子群的优化公式为：

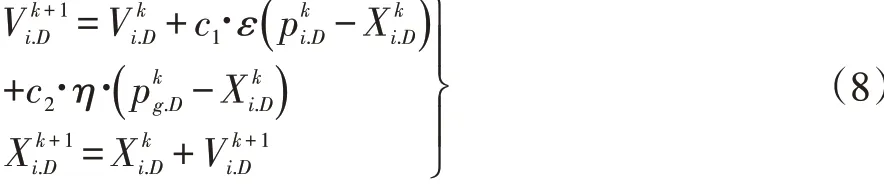
式（8）中，k为迭代次数；c1和c2分别为个体学习因子与群体学习因子；ε和η为0到1之内的随机数；初始化时设置粒子飞行速度最大值为Vmax。

（2）AFSA原理

鱼群算法通过模仿鱼群的觅食、追尾和聚群行为来寻优目标函数的全局极值。在指定水域中，鱼群通过上述三种基本行为能快速聚拢在食物最丰富的地方。鱼群算法对目标函数无特殊要求，且在寻优过程中用三种行为能更智能地定位最佳食物源，有着较快的收敛速度。

鱼类通过视野的变化不断调整行进方向或速度来寻找食物是它基本的生物学行为，设第i（i=1，2，3...n）只鱼在指定区域内不停搜索食物，其当前位置状态为，在其视野领域内随机选择下一个行进位置，则在当前位置与下一随机位置下对应的寻优函数值分别为，当求解优化问题的极大值时，若在当前状态下的所有解范围内，则向该区域前进一步；否则，重新选择下一个随机位置状态继续判断优化条件是否满足。若随机N步后依然未寻到更大解，则随机前进一步。觅食行为Fp的更新公式为：

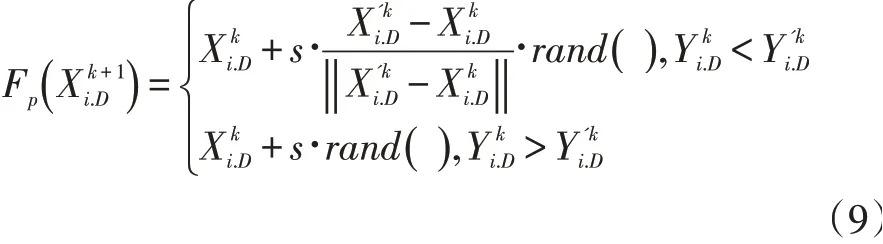
鱼群在活动过程中通过聚群可以保证鱼群的整体性以避免危险和合作觅食。设人工鱼当前位置为在指定视觉范围内确定鱼群数量nf与鱼群的几何中心如果nf/n＜δ（拥挤度因子）且适应度函数（fXc）>f（Xi），即此鱼群中心食物丰富且鱼群较少，则向该中心位置聚拢，否则继续觅食。聚群行为Fs更新公式为：

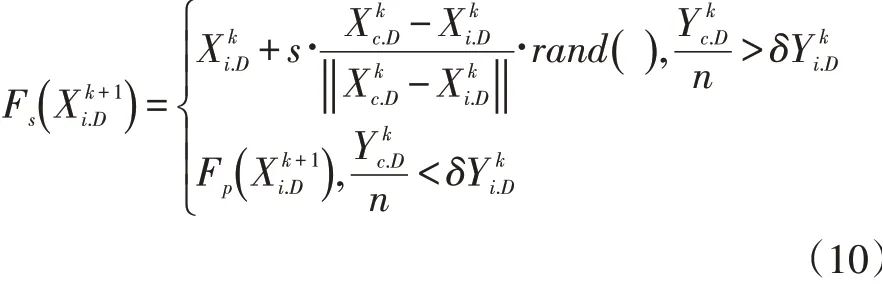
鱼群中一定数量的鱼群发现食物时，其周围的鱼群会紧随而至。设第i只鱼在寻找食物时状态为搜索临近范围内的鱼群数量与食物浓度最大的鱼群若伙伴食物浓度达到临界值且鱼群拥挤度系数低于设定值，则向该方向前进一步，否则执行觅食行为。追尾公式为：

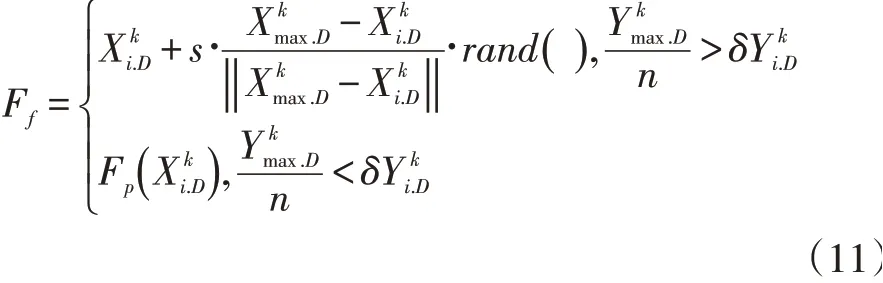
（3）PSO-AFSA混合算法

提出的PSO-AFSA算法综合了PSO和AFSA的优点，首先随机生成一定数量的初始鱼群，计算所有鱼群的适应度函数值以挑选出部分精英鱼群。先使用PSO对目标函数值较高的精英鱼群依次更新，设置Nmax为精英鱼群迭代次数；普通鱼群则执行AFSA更新，每一轮全体鱼群更新后依适应度函数值进行排序，筛选出新的精英粒子，直到迭代结束。PSO粒子通过学习本身历史最佳值与群体最佳值来改变行进的方向和速度，该属性能够大幅度加快算法的收敛速度；AFSA具备良好的全局收敛能力，能较快地跳出局部最优点，而挑选部分精英粒子可以综合两种算法的优点来加快收敛速度。

1.3 基于改进算法的二维熵多阈值快速图像分割方法

提出了基于改进粒子群人工鱼群的二维熵多阈值快速图像分割方法，将图像的多阈值选择问题定义为改进算法的目标函数，即对多维度函数H（s1，t1，...sk，tk）的最大值寻优问题。

将二维熵函数H（s1，t1，...sk，tk）设置为粒子群人工鱼群算法的目标函数，粒子群人工鱼群算法的寻优结果为使得二维熵适应度函数值最大的鱼群位置X（s1，t1，s2，t2，...sk，tk）。其中k为二维熵阈值个数；（s1，t1，s2，t2，...sk，tk）即为所求最佳二维熵阈值。基于改进算法的分割法具体步骤如下：

（1）初始化粒子群人工鱼群算法参数，随机生成全体粒子并计算出二维熵函数值，排序筛选出精英粒子和普通鱼群粒子，设置拥挤度因子、视觉范围、粒子群迭代次数及总迭代次数等相关参数；

（2）分别计算精英粒子和普通鱼群粒子的适应度函数值，即对应的二维熵函数值；

（3）对精英粒子进行PSO迭代更新，其最佳适应度值为Yb；

（4）对普通鱼群用聚群公式和追尾公式进行更新，排序后选择最大值Y为最佳更新结果；

（5）比较Y和Yb，判断适应度最大值是否发生改变，若变大则赋值给Yb，否则普通鱼群执行觅食行为；

（6）将更新后的精英鱼群最佳值与普通鱼群最佳值Yb比较，若更大，将该值赋予Yb；

（7）全部鱼群更新完成后，判断是否达到迭代最值，达到迭代最大值则输出最佳适应度值Yb，否则转至步骤（3）；具体流程图如图3。

2 实验结果与分析

2.1 基于改进算法的二维熵多阈值快速图像分割实验

为验证本文提出算法对二维熵多阈值分割的时效性与阈值选择的准确性，实验对Lena图、Peppers图、Baboon图、Terrace图和QFN（Quad Flat Non-Lead）芯片封装图像进行分割，并与穷举分割法和粒子群分割法对比。Lena、Peppers和Baboon图常用于图像处理，Terrace图含多个目标且背景不明显，QFN是常见芯片封装，使用时易受到刮划，造成外部伤痕，这些缺陷易造成焊接不牢、接触不良等现象，且返修难度大，检测其表面划痕能提高芯片的回收率，具有一定的现实意义。

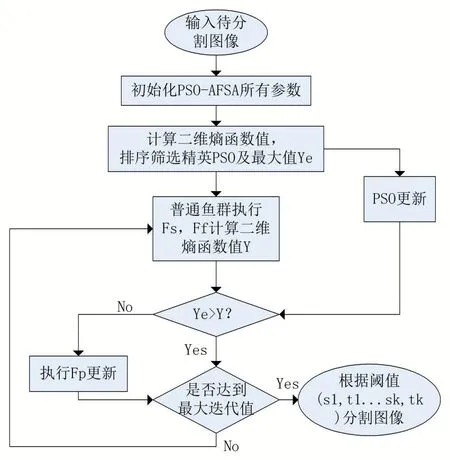
图3 基于PSO-AFSA的二维熵多阈值图像分割算法流程图

对五幅图像进行单阈值、双阈值及三阈值分割，初始化时，将PSO-AFSA具体相关参数设置如下：总粒子数N=50，精英粒子Ne=10，总迭代次数Nmax=100，单步步长s=0.1，速度范围[-Vmax，Vmax]=[-5，5]，随机数rand=0.5，个体惯性权重C1=1.5，群体惯性权重C2=1.5，随机量ζ=η=0.5，鱼群视觉最大范围V=10。分割后的图像如图4所示，最左为原始图，往右为依次增加阈值的分割图。

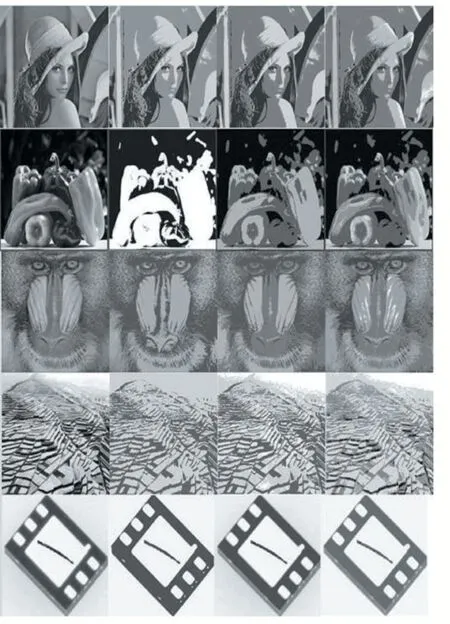
图4 分割实验结果图

2.2 二维熵穷举算法、粒子群二维熵多阈值分割法实验对比

为验证本文算法的准确性，将其与穷举分割法、PSO多阈值分割法进行对比实验。

二维熵穷举分割法在函数定义域内逐个计算最大值，保证目标函数最优值的准确性，穷举法的计算量随阈值增多而呈指数增长，本文计算复杂度依次为O（L2）、O（L4）、O（L6），L=255，可知，双阈值及以上时穷举法由于计算量过大将不再适用；PSO二维熵多阈值分割法是基于PSO的二维熵多阈值图像分割方法。

五幅图像分割后的阈值及二维熵值如表1所示。

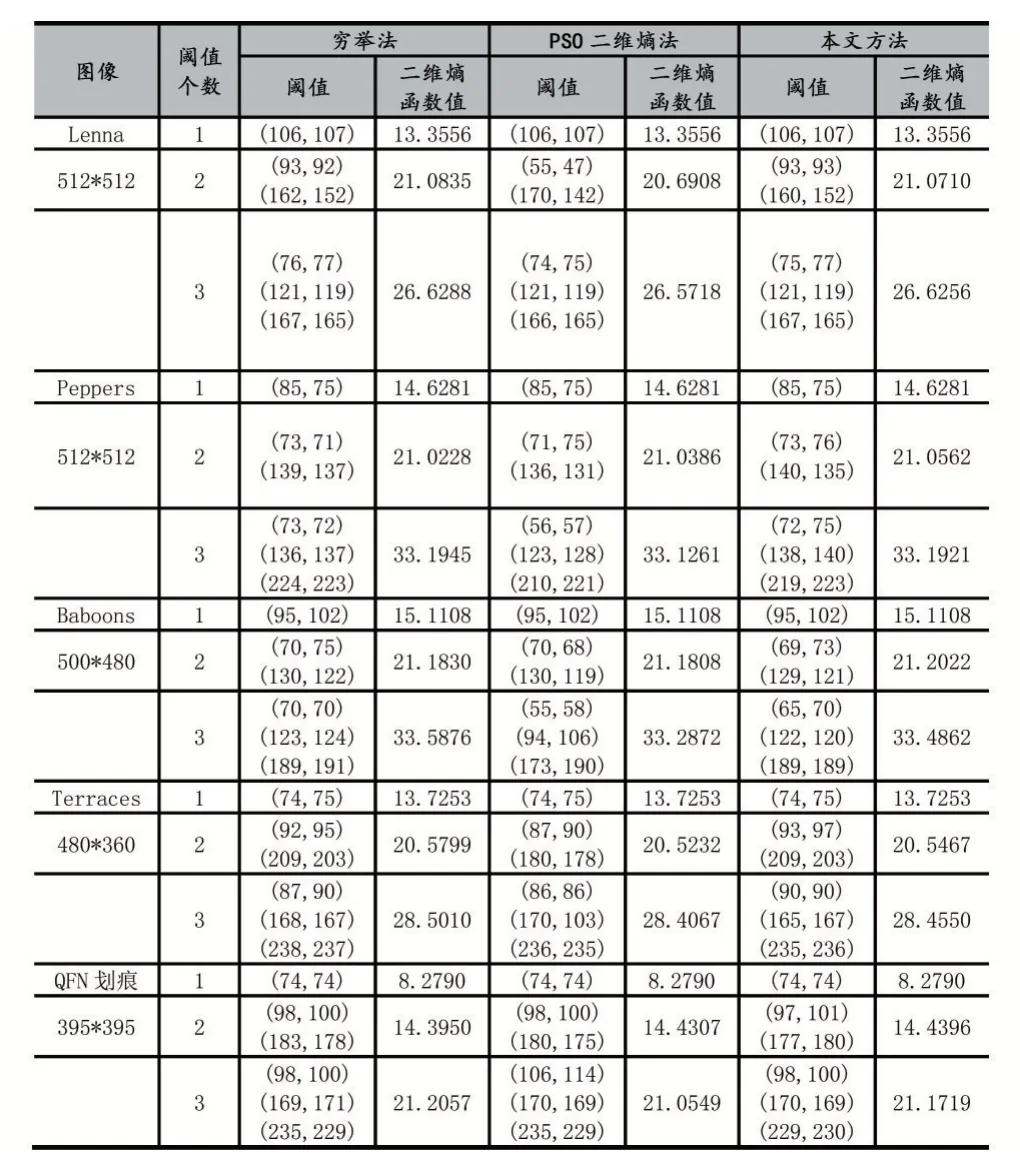
表1 3种方法计算的阈值与二维熵函数值

由表可知，使用PSO分割法的二维熵函数值的平均误差为0.29%，改进算法的二维熵函数值的平均误差为0.04%，新算法寻得的阈值更接近于穷举算法的阈值。因此，改进算法的精确性较基于PSO的分割法更高。

图像分割后，单凭人眼无法准确判断分割效果，常采用信噪比准则测试算法分割效果，间接评价算法的分割效果。图像处理中信噪比准则的表达式为：

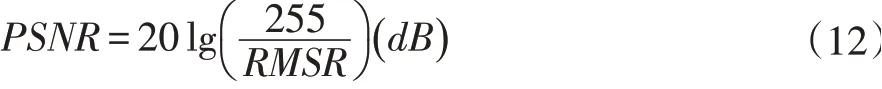
其中：

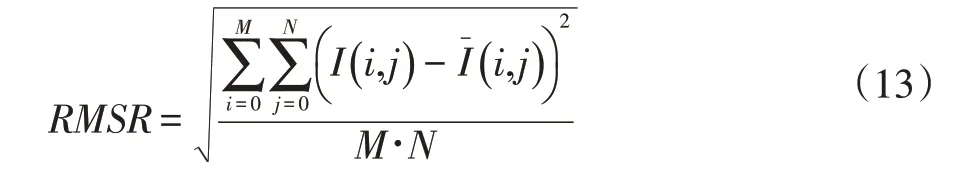
I（x，y）、I（x，y）分别表示原图像与分割后的图像。

三种方法分割图像的PSNR值与计算时间如表2所示。可知，改进算法在单三阈值、双阈值和三阈值分割都比穷举分割法快；与PSO分割法时间接近。但改进算法PSNR值都比穷举法与PSO分割法高。

综上，基于改进粒子群人工鱼群的二维熵多阈值分割法在耗时上有了极大提高，且PSNR与分割精度均优于基于PSO的分割法，能更快速有效地分割多目标图像。

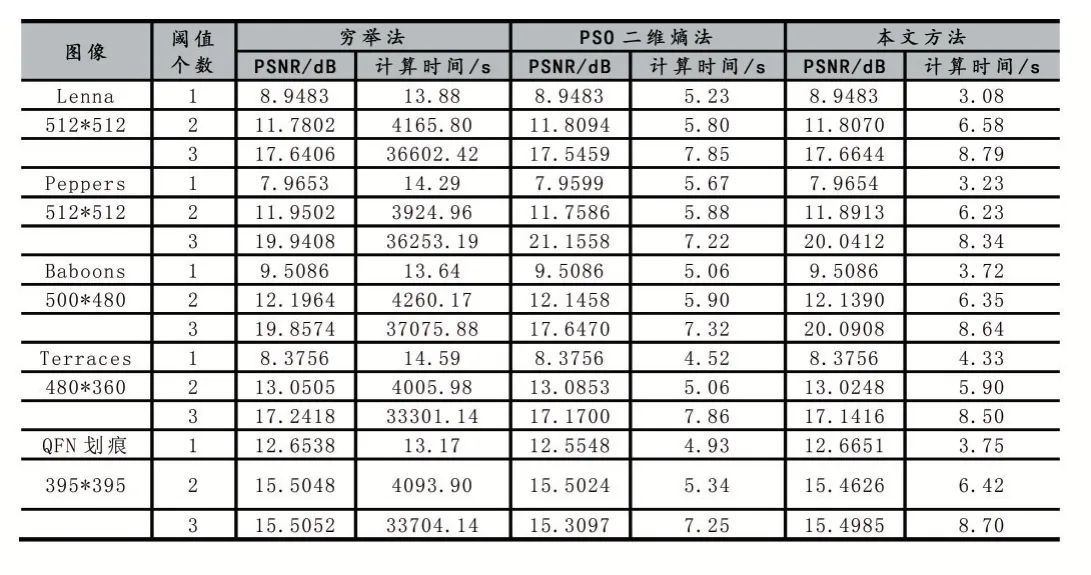
表2 3种方法的计算时间与对应PSNR值

3 结语

对模糊图像和复杂图像阈值分割随阈值数量增加而运算量大导致耗时长的问题，提出基于PSO-AFSA混合算法的二维熵快速分割法。解释了二维熵单阈值分割的选取原理，并延伸至多阈值分割。然后，引入两种仿生优化算法，将粒子群能参考个体最佳值与群体最佳值的特征引入到人工鱼群算法，解释并比较两种算法的寻优原理与优缺点。使用该改进算法对典型图像进行分割并与穷举分割法和PSO分割法比较。结果表明，提出的混合算法分割效果良好，得到的二维熵函数值平均误差为0.04%，分割速度比穷举分割法快两个数量级。因此，使用改进粒子群人工鱼群算法的二维熵阈值分割能更快速有效地分割模糊图像和多目标图像。