基于单神经元的高速列车速度跟踪控制

王雪奇，莫晓婷，梁新荣，董超俊

（五邑大学智能制造学部交通工程系，江门529020）

0 引言

高速铁路建设日新月异，列车自动驾驶（ATO）成为当前的研究热点，ATO系统中一个重要的研究内容是列车速度跟踪控制，相关的研究包括列车建模、优化和控制。

要做到速度的精准跟踪，首先要对列车运行过程进行建模。高速列车采用的建模方法主要有传递函数建模[1-2]、单质点建模[3-4]、多质点建模[5]和数据驱动建模[6]。上述建模方法都有各自的特点，传递函数建模过程简单但准确性较低，目前应用较少；单质点建模将高速列车看作一个质点，忽略了车厢之间的内力，建模过程不复杂，准确性较高，是目前应用最多的建模方法；多质点建模考虑车厢之间的相互作用力，计算精度高，但建模过程复杂，不利于定时求解，往往要对多质点模型进行简化；数据驱动建模是利用列车运行时产生的海量数据，用人工智能的方法进行建模，建模精度取决于所用的信息处理技术。

在列车优化和控制方法上，随着智能时代的到来，智能优化算法、模糊控制、神经网络控制等方法受到了研究人员的重视。王花等人[7]用遗传PID设计列车速度控制器，遗传算法的缺点是早熟，它可能找到局部最优而非全局最优的PID参数。段玉琼等人[8]用蜂群算法优化高速列车能耗，蜂群算法的缺点是可能滞留在局部最优解附近。Dong等人[9]用模糊控制实现列车速度跟踪，模糊控制的缺点是控制性能过多地依赖控制规则的制定。肖龙等人[10]用RBF神经网络研究列车速度跟踪，神经网络的缺点是控制性能依赖于样本数据的选取，并且学习算法有进一步的改进空间。马晓娜等人[11]用模糊PID控制实现ATO优化控制，模糊PID控制的缺点是控制变量依赖于所选取的隶属度函数。李中奇等人[12]用广义预测控制对列车速度曲线进行跟踪控制，广义预测控制的缺点是计算过程比较复杂。

本文采用单质点模型，用单神经元PID控制设计高速列车速度跟踪控制系统，并编写仿真程序验证该方法的控制效果。

1 高速列车单质点模型

单质点模型将一辆列车看作一个质点，不考虑车辆与车辆之间的作用力。根据受力情况和牛顿第二定律，可设列车单质点模型表达式为：

其中，m、v和t分别表示列车总质量、列车运行速度和时间；F和f分别表示牵引力/制动力和列车运行阻力；f0、fi和fr为分别是基本阻力、坡道阻力和弯道阻力。

基本阻力主要由轮轨摩擦力和空气阻力组成，一般以单位基本阻力表示，其计算公式为：

其中，g为重力加速度值；a、b和c是基本阻力系数，因为单位基本阻力为每1000N重力上的基本阻力，因此式（2）分母是1000。

坡道阻力fi计算公式为：

其中，α表示坡道角度值。

弯道阻力fr计算公式为：

其中，A为450-800之间的常数，一般取600；R为轨道曲线半径。

2 基于单神经元的速度跟踪控制系统设计

2.1 神经元三种学习规则

单神经元结构简单，是组成神经元网络的基本单位，神经元具有自学习能力，这种自学习能力使得神经元网络对外界环境具有适应能力[13]。神经元的学习能力有对应的学习规则，通常有如下三种学习规则。

无监督的Hebb学习规则，其表达式为：

其中，Δwij（k）为神经元i与j之间连接权值的增量，η是学习率，oi（k）和oj（k）分别对应神经元i和j的激活值。

有监督的Delta学习规则，其表达式为：

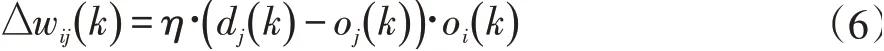
其中，dj（k）为神经元j的期望输出，它对应有监督的导师信息。

有监督的Hebb学习规则，其表达式为：

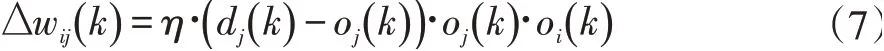
显然，式（7）的学习规则是式（5）和式（6）的学习规则的组合。

2.2 单神经元自适应PID控制

图1 示出了单神经元PID控制方框图，这是含有一个神经元并包含反馈的控制系统。

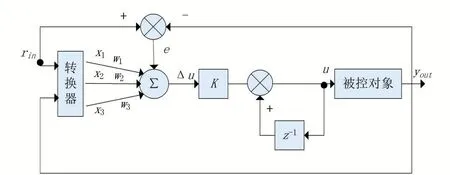
图1 单神经元PID控制

图1 中，rin为控制系统的输入信号，yout为控制系统的输出信号，e为误差信号，误差信号等于输入信号与输出信号之差，即和x3是转换器的输出，其大小分别为和w3为权系数，u为被控对象的输入，Δu是u的增量部分，K为单神经元的比例放大因子；z-1表示一步延时算子。权系数w1、w2和w3的更新是采用2.1小节的有监督Hebb学习规则，具体的学习算法如下：

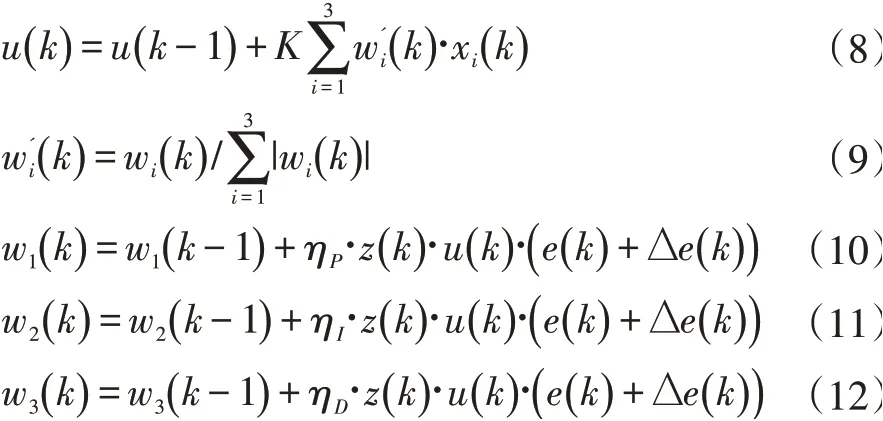
其中，ηP、ηI和ηD分别表示比例学习因子、积分学习因子和微分学习因子；z（k）表示误差信号，即表示误差的增量，其大小为第k步的误差减去第（k-1）步的误差，即比例放大因子K的选取比较关键，因为K值的大小会影响系统的响应速度，当K值过大时，系统响应速度加快，但会引起系统的超调量变大，甚至还会使系统出现不稳定的现象；当被控对象属于大延时系统时，应该减小K值，这样可以增加系统的稳定性，但过小的K值又会使系统响应速度变慢。在实际应用中，比例放大因子K主要是根据经验用试凑的方法来选取合适的值。

2.3 列车速度跟踪控制系统设计

列车在实际线路上运行时，与期望的速度-位置相一致，列车有一个期望的时间点速度vd，期望速度vd可根据实际线路运行情况采用优化的方法得到。当指定某个期望速度vd时，ATO系统采用某种控制策略使列车实际速度跟踪vd，并且使跟踪误差尽可能减小。图2是采用2.2小节单神经元PID控制设计的列车速度跟踪控制系统的方框图。

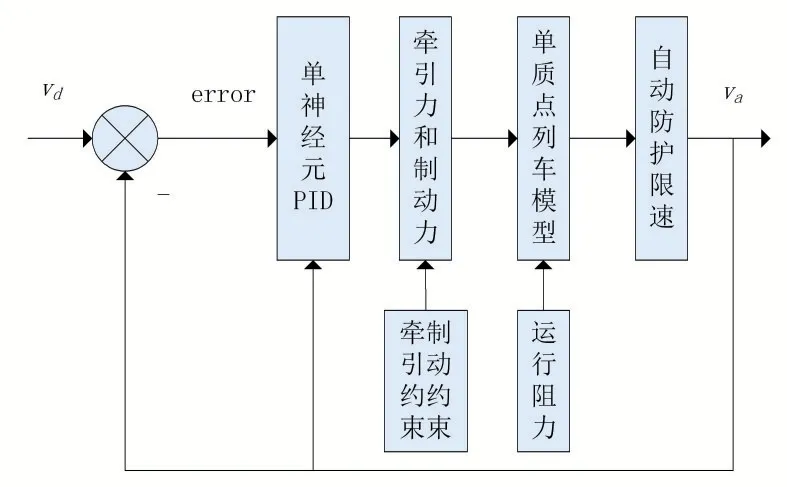
图2 基于单神经元PID的速度跟踪控制系统

图2 中，vd和va分别是列车的期望速度和实际速度，error是列车期望速度与实际速度的差值，即error=vd-va；图2的vd和va分别对应图1的rin和yout，图2的error对应图1的e，图1的被控对象就是图2的单质点列车模型。图2的单神经元PID控制采用2.2小节的学习算法产生列车所需的牵引力和制动力，具体学习过程如下：对于已知的列车期望速度样本数据vd，根据vd和列车实际速度va的差值产生误差信号error，即error(k)=vd(k)-va(k)；根据误差信号error，可计算出x1，x2和x3，即x1(k)=error(k)，x2(k)=error(k)-error(k-1),；再根据式（10）至式（12）更新单神经元的权值w1、w2和w3，然后根据式（8）和式（9）产生新的控制量u（k），u（k）对应列车的单位牵引力和制动力，该牵引力和制动力作用于单质点列车模型并使列车产生新的速度va，从而完成一次反馈循环。图2所示的控制系统是一种非线性反馈系统，vd是输入变量，va是输出变量，牵引力和制动力是控制变量，用单神经元PID控制产生合适的牵引力和制动力可使va跟踪vd，系统具有很小的跟踪误差和优越的跟踪性能，并能抑制扰动噪声等干扰信号。

3 仿真结果

考虑图2的列车速度跟踪控制系统，并对其实施仿真实验，图2的列车模型采用某型号动车组的基本参数，该参数由北京交通大学提供，然后根据第2节的算法编写仿真实验程序。具体的列车参数为：列车质量840t，最大运行速度400km/h，自动防护限速405km/h，基本 阻 力 系数a、b和c分别为0.53、0.0039和0.000114；列 车 牵 引 特 性 为：当0＜v＜150km/h时，Fj=-300v+505000(N)；当150km/h≤v＜400km/h时，Fj=69000000/v(N)。列车制动特性为：当0＜v＜150km/h时，Fz=835000(N)；当150km/h≤v＜250km/h时，Fz=-850v+962500(N)；当250km/h≤v＜400km/h时，Fz=-400v+850000(N)。图2的列车期望速度vd同文献[9]和文献[10]，仿真实验采用的电脑为戴尔Intel Core i3，内存配置仅为4GB，在这台电脑上多次运行仿真实验程序的时间在0.1～0.2秒之间，说明单神经元控制系统的响应速度快、响应时间短，适合在线运行和测试。

图3 至图6为仿真实验过程得到的速度跟踪曲线、距离跟踪曲线以及速度误差和距离误差。从这些仿真效果图可以看出，单神经元控制系统具有好的速度跟踪性能和距离跟踪性能，速度跟踪误差都在零附近上下波动，多数时间点的速度误差接近零，少数时间点的速度误差有一点波动，但速度误差的最大值也都控制在±4km/h的范围内，且距离误差的最大值也都控制在±4m的范围内。速度跟踪误差的平均值为0.1607km/h，距离跟踪误差的平均值为0.8821m，最大速度误差为3.7618km/h，最小速度误差为-2.9953km/h。

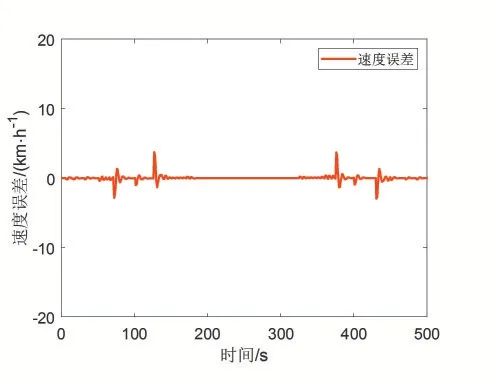
图4 速度误差

图5 距离跟踪效果图

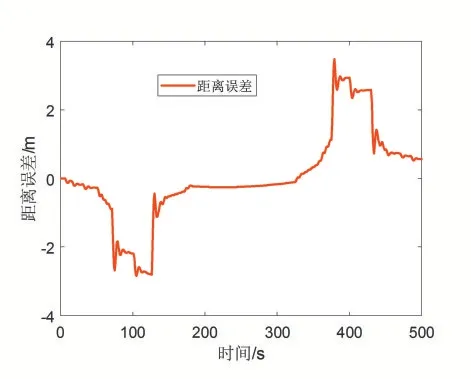
图6 距离误差

最后在仿真环境和参数设置一样的条件下，对传统PID控制、文献[10]的RBF神经网络PID控制以及本文的单神经元PID控制这三种控制方法的控制效果进行对比分析，对比结果如表1所示。

表1 三种控制方法对比

通过实验对比可知，虽然三种方法都能实现速度跟踪和距离跟踪，但控制效果和跟踪误差有较大的区别，传统PID控制具有较大的速度误差和距离误差，跟踪效果不理想，而且存在PID参数选取困难的问题。文献[10]的方法具有较好的跟踪性能和控制效果，但仍有进一步改进的空间。相比之下，本文的单神经元控制方法具有最小的速度误差和最小的距离误差，且调试过程并不复杂，非常适合高速列车速度跟踪控制。

4 结语

本文将单神经元控制和非线性反馈控制相结合，设计了列车自动驾驶中的速度跟踪控制系统。该方法采用的单质点模型考虑了轮轨摩擦力和空气阻力，也考虑了坡道阻力和弯道阻力，提高了单质点模型的准确性。单神经元PID控制采用有监督的Hebb学习规则调整权系数，提高了系统的学习能力和对环境的适应能力。相对于开环控制，非线性反馈闭环控制提高了控制系统的控制性能，增强了系统抑制干扰信号的能力。利用实际动车组参数和相关文献提供的列车期望速度数据进行仿真实验，验证了单神经元控制系统优越的速度跟踪性能。三种控制方法的对比仿真实验表明，本文的方法具有最小的速度跟踪误差和距离跟踪误差，而且系统的响应时间短，适合列车在线运行控制。