基于STM32的小型四轴飞行器编队控制系统设计

陈韩悦，刘晓航，王品智，夏昊鹏，赖晓晨，惠煌

（大连理工大学软件学院，大连116000）

0 引言

相较于传统载人飞行器，无人机具有体积较小、动作灵活、适用面广泛、成本低廉等优势，且因其无人驾驶的特性，可以由控制人员进行远程操作，适用于执行高风险的特殊任务，能够有效保障工作人员的生命安全，无论在民用还是军用领域都越来越受到人们的青睐[1]。

无人机群相较于单架无人机，具有更大的视角，能够全方位地观察目标动向，同时针对硬件故障、无线通信受阻、机体动力源失效、环境突变等突发情况具有更高的适应性和容错率。但无人机群协同控制相较于单架无人机的飞行控制，具有更多的理论和工程难点，如无人机间的通信系统建设、机群队形的控制保持等。同时，针对无人机数量的增多，如何有效控制成本，也是需要考虑的问题。

1 研究现状

针对不同规模、不同形式的网络拓扑结构，应采用不同的编队控制策略和通信方式[2]。当前对于无人机群编队控制领域的研究，主要侧重于对控制方法的研究，而不过多涉及对无线网络的拓扑结构研究或通信时延问题的探讨。在通信研究领域，对无人机群自组网络的研究很少涉及对无人机编队控制策略的需求分析。因此在对无人机群自组网络的通信技术方面的研究亟待深入。

本文将基于STM32为核心的小型四轴飞行器，利用PID控制技术、2.4G射频通信技术、地磁校准算法，设计一款四轴飞行器编队控制系统，实现四轴飞行器的小规模编队飞行。飞行器能够实现基本的飞行功能，在空间中稳定悬停、移动和转向；若干架飞行器能够组成“主-从”编队；在飞行过程中，飞行编队能够利用环境磁场实时校准统一航向，维持队形的稳定。

2 研究现状

2.1 系统结构

为实现四轴飞行器的编队控制，需要实现无人机飞行控制、飞行器间通信自组网络以及机群队形保持等基本模块。系统整体结构如图1所示。

图1 系统整体结构图

2.2 无人机控制

在无人机控制部分，如图2所示，系统主要使用姿态解算算法以及闭环控制算法，有效实现了单架无人机飞行过程中的快速自稳，使无人机拥有向期望坐标飞行并在目标位置保持稳定的能力。

图2 无人机控制模块结构图

2.3 通信自组网络

如图3所示，在无人机自组网络中，本项目设计了集中式的网络拓扑结构。使用了2.4G无线通信模块nRF24l01及nRF51822的双向链通信方式，实现了以遥控器为控制中心，集中控制无人机群的控制策略。

图3 无人机网络拓扑结构图

2.4 机群队形保持

在无人机群队形的保持方面，系统主要利用无人机飞行控制模块中的空间坐标PID控制，并利用地磁特征对航偏角进行实时修正。本模块结构如图4所示。

图4 机群队形保持模块结构图

3 系统实现

3.1 无人机飞行控制方法

（1）姿态解算

无人机的微型控制单元通过IIC总线读取九轴传感器MPU9250的采样数据。通过IIR低通滤波后，对加速度计的原始数据进行处理，并对陀螺仪的原始数据进行偏置调整。最后将二者处理后的数据融合，得到无人机的姿态角。其中，为减轻欧拉角带来的正余弦计算负荷，以及欧拉角存在的GimballLock问题，采用四元数形式进行姿态计算，在最后将姿态角的四元数形式转换为欧拉角形式。

（2）角度和角速度串级PID控制

PID闭环控制主要分为三个部分：比例控制、积分控制、微分控制，其数学公式为：

其中Kp为比例系数，Ki为积分系数，Kd为微分系数为控制量期望值与实际值的误差。在此定义PID算法的接口函数返回值为经过本周期更新后的输出量，传入的参数包含相应PID控制器的比例、积分、微分系数，其设定需要根据四轴飞行效果进行调节，同时还传入了控制量的期望值与实际值的误差。

在此基础上，设计角度环PID和角速度环PID控制方法，其逻辑结构如图5所示。

图5 串级PID控制方法

角度环PID控制器的输入变量为角度期望值以及测量角度值，其中期望角度来自遥控器发送的控制信号，测量角度来自姿态解算得到的无人机姿态，控制器输出信号为期望的无人机旋转角速度。

角速度环PID控制器的输入为角度环PID控制器输出的期望角速度和实际角速度值，实际角速度值可由陀螺仪进行测量。

（3）空间坐标PID控制

对无人机的三维坐标控制，分为距地高度控制与平面XY坐标控制。PID控制方法的输出量为XYZ三方向上的期望运动速度，通过特定的转换方法，可以将其转化为无人机的期望横滚角、期望俯仰角以及油门增量。其转换方法的代码实现如下所示，其中attitude为无人机的期望姿态角，thrustRaw为无人机的油门增量，setpoint为期望坐标点：

（4）姿态控制量和油门值整合

本设计中的无人机飞行模式采用X型结构，其中电机转向与飞行器姿态正方向如图6所示，其中箭头方向表示姿态角的正方向。

图6 电机转向与姿态正方向

每个电机的控制量，由横滚角控制输出量、俯仰角控制输出量、航向角控制输出量、基础油门控制输出量共同决定。根据图6所描述，电机转速变化对无人机的飞行影响如表1所示。

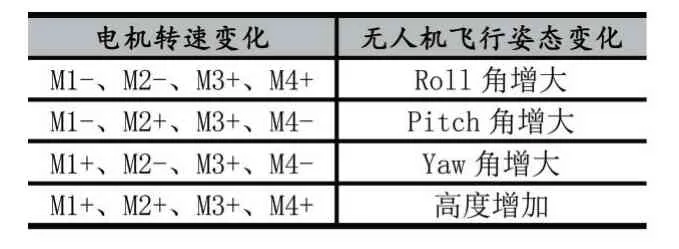
表1 电机转速对无人机飞行影响

由此可以计算出对各个电机的控制量，计算方法如下：

其中control为姿态控制量的结构体，它的thrust元素为飞机定高油门基础值和油门增量的和，roll、pitch、yaw为飞机的期望姿态角。

3.2 无人机群自组网络实现

（1）无人机群的自组网配置

本设计采用2.4G射频通信方式进行遥控器与无人机之间的信息交互。采用集中控制的方法，且为避免信号冲突采用了异步分时复用的通信方案。遥控器作为发送端，为控制中心，在每个周期对编队中的无人机轮询地进行无线数据交互。在信宿区分方案上，为编队内各架无人机配置唯一通信地址。

在无线通信的配置上，无人机以及遥控器统一设置无线通信的数据传输率为250kbps，无线通信的通信频段为信道2。在通信地址的配置上，各架无人机需要设置唯一的通信地址，其地址配置与拓扑结构如图7所示。

图7 无人机组网拓扑结构

当nRF24l01工作在Enhanced ShockBurst的发送模式时，仅使用通道0作为接收通道，且需要保持发送地址与通道0的接收地址一致，在发送一个无线报文后，要求在一定时间范围内，收到接收设备发出的应答信号，若在规定时间内未收到确认，则自动重发，若到达重发次数上限仍未接收到应答信号，则认为该报文发生丢失。在对nRF24l01的配置中，需设置其应答接收时间为1500us，重发次数上限为3次。

经过以上工作即可完成对无人机编队组网的无线通信配置。

（2）无线通信程序框架

针对地面控制中心，其无线通信的工作流程可概括为：

①发送地址配置：针对编队中的指定无人机，将发送地址设置为无人机的通信地址。

②获取数据帧：从控制信号队列中获取数据帧，如果信号队列为空，则获取空数据帧。

③数据帧发送并等待应答信号：将②中获取的数据帧送入nRF24l01的发送寄存器中，并使能无线传输，之后等待应答信号，若收到应答信号，则将该数据帧放入接收数据队列。

④发送判断：根据是否成功收到应答信号，改变全局标识符。

⑤指定下一个无人机。

3.3 无人机协同编队飞行控制方法实现

采用长机-僚机飞行策略，长机的坐标包括：距地相对高度、机体坐标系上的X坐标、Y坐标，其可由气压计、光流传感器采样获得。不考虑通信阻塞、数据丢包等问题，长机以1ms为周期，向遥控器发送自身的坐标数据，数据帧通过帧头的功能字字段加以区分，遥控器接收到长机的坐标数据后，计算僚机期望的飞行轨迹，并依次向所有僚机进行转发。僚机的闭环飞行控制方法如图8所示。

图8 僚机的闭环飞行控制

3.4 地磁特征修正航偏角的实现

（1）通过磁力传感器数据计算航向

地磁场在一定范围内可以看作是空间中的匀强磁场，因此可以作为测算的基准。下面引入两个坐标系：磁地理坐标系（m系）及飞行器坐标系（b系）。其中m系以水平面为XY平面，以磁场在水平面上的投影方向为X轴正方向。b系以飞行器机身平面为XY平面，机头朝向为X轴正方向。

当m系与b系重合时，在飞行器上安装磁力传感器，使得磁传感器的测量值Mb如式（2）所示：

其中MN为当地磁场的水平分量大小，MD为当地磁场的垂直分量大小[3]。

此后，无论飞行器处于任何姿态，磁传感器的输出均可以表示为：

根据三角函数知识，利用飞行器的横滚角γ和俯仰角θ，可得：

从而得到地磁场矢量在X轴和Y轴的分量为：

则磁航偏角为：

ψm为b系X轴正方向在m系XY平面上的投影与m系X轴正方向的夹角。由于地磁场在一定范围内可以视为匀强磁场，因此只要编队内各飞行器ψm值保持一致，即可维持航向角的统一。

（2）磁场校准算法

由3.4（1）中的描述可知，若b系XY平面与m系XY平面平行，且m系X轴与b系X轴正向平行时，磁力数据应为式（2）所示，显然在二者反向平行时，磁力数据为：

但由于磁场数据会受到外界的干扰，而其中最主要的是飞行器自身电子器件所产生的恒定磁场对其干扰。这一点在图像上表现为球体位置的平移和形状的拉伸，即实际数据样本在采样空间中所显示的图像为中心位于空间中某一点的椭球。故我们不能将磁力计所获取的数据直接用于计算磁航偏角ψm。

因此，需要求出该椭球的表达式，以便对磁力计数据进行修正。本项目采用最小二乘法进行椭球拟合。

通过理论分析和实验证明，磁场椭球主要经历了拉伸和平移变换，而没有经历旋转变换，因此可以将其表示为：

其中(x0,y0,z0)为椭球的中心，a,b,c为三个半轴的长度。

将式（8）展开，可以得到：

将一组实际测量的磁场数据带入到上式：

显然，若a=0则表明样本点落在椭球表面，若a≠0则表示存在偏差。由最小二乘法思想，我们将等式两边分别平方进行累加得用来表示总误差。为使Q取极小值，令Q对A,B,C,D,E,F的偏导数均为0，可以得到如下方程组：

将方程组（11）整理成矩阵形式：

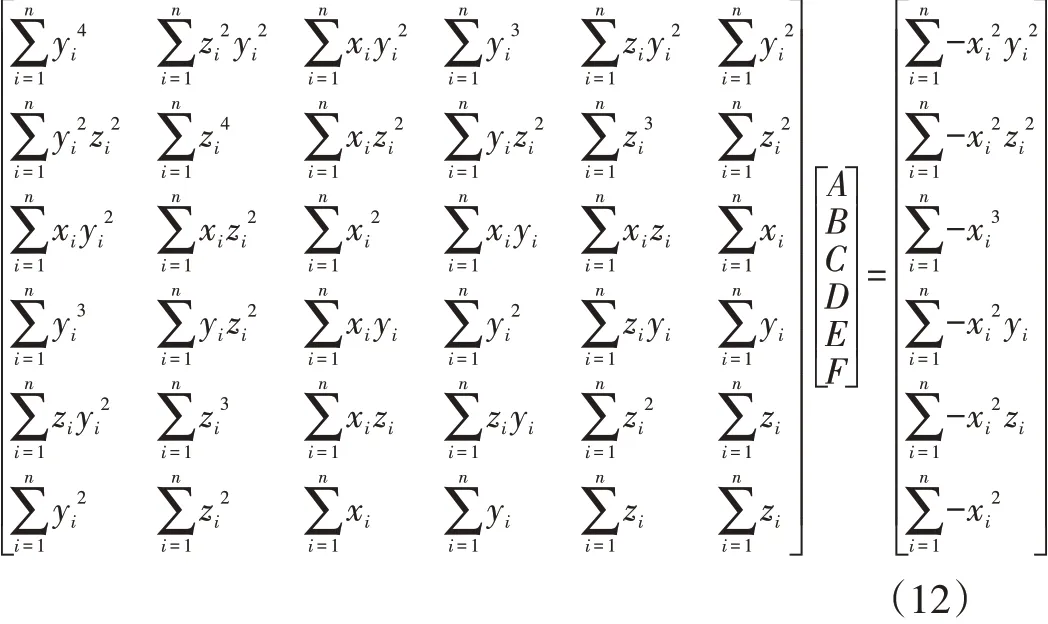
利用高斯消元法，将矩阵转换成上三角形式，回代后即可求解出A,B,C,D,E,F的值。由此，便获得了该椭球方程的一般式，为了对磁场传感器的数据进行修正，需要将其化为形如式（8）所示的标准式。在得到及a,b,c后，便可将原始数据映射到标准球面上，从而实现磁航偏角ψm的计算。

4 结语

基于STM32的小型四轴飞行器编队控制系统，提供了四轴飞行器的飞行控制、飞行器间通信组网以及机群的队形保持等基本模块，实现了小型四轴飞行器的编队飞行。系统所设计的利用地磁场校准航向角的思路具有一定的创新性。系统所涉及的硬件资源较为精简，有利于四轴飞行器编队的小型化和低成本化，具有一定的现实意义和实用价值。