基于深度强化学习的投资组合管理研究

王康，白迪

（四川大学计算机学院，成都610065）

0 引言

美国经济学家马科维茨（Markowitz）1952年首次提出投资组合理论，并进行了系统、深入和卓有成效的研究。投资组合管理是不断将资金重新分配到许多不同的金融资产中的决策过程，旨在抑制风险的同时最大化收益[1]。在发达的证券市场中，马科维茨投资组合理论早已在实践中被证明是行之有效的，并且被广泛应用于组合选择和资产配置。但是，我国的证券理论界对于该理论是否适合于我国股票市场一直存有较大争议。

如何使投资组合在一定的风险范围内获得最大的收益，是一个非常值得关注的问题。同时，由于影响证券活动的复杂因素很多，如收益的风险和不确定性，因此很难建立合适的投资组合管理模型。深度强化学习最近因其在电子游戏[2]和棋盘游戏[3]方面的卓越成就而备受关注。但是这些是离散动作的强化学习问题，不能直接应用于连续动作的投资组合管理问题。虽然投资组合管理的动作可以离散化，但是离散化被认为是一个主要缺点，因为离散动作并不能使得强化学习代理进行充分探索，从而增加了风险。例如，一种极端的离散动作可以定义为将所有资本投资到一种资产中，而没有将风险分散到其他资产上。所以为了尽可能地分散风险，强化学习算法的动作必须是连续的。我们利用了深度强化学习的策略梯度算法（PG）[4]和最近提出的一种双延迟深度确定性策略梯度算法（TD3）[5]来实现连续动作的投资组合管理，TD3算法的性能在Silver提出的深度确定性策略梯度算法（DDPG）[6]上有进一步提升。

本文将PG和TD3算法应用于投资组合管理中，并通过与UCRP、Follow the Winner、Follow the Loser和Buy and Hold等策略进行对比实验。实验选择中国市场龙头股票中成交量较大的5支股票和国债作为资产包，结果表示TD3和PG算法在测试集上年利率分别为84.71%和55.06%，明显高于其他对照组。

1 相关工作

强化学习是一种通过与环境交互学习，不断进行反复试验逐步优化，并利用马尔可夫决策过程来解决问题的方法，在与环境的交互过程中通过学习策略以达到回报最大化。传统强化学习用迭代贝尔曼方程求解值函数的方法，在状态空间过大时计算代价太大，通常使用线性函数逼近器来近似表示值函数。深度强化学习是用深度神经网络作为非线性函数逼近器去近似表示值函数或策略，从而将深度学习的感知能力和强化学习的决策能力相结合的方法[7]。

基于深度强化学习在游戏领域的巨大成功，它也受到金融界的广泛关注。在传统的投资组合管理中，投资者需要关注许多金融投资的领域知识，给大多数投资者带来了挑战。而利用深度强化学习，投资者可以除了基本交易规则外不需要关注过多的领域知识。首先是Pendharkar P C等人使用传统的强化学习方法构建了一个包含两个资产的个人退休投资组合管理，他们使用了离散状态和离散动作的SARSA（λ）和Q（λ），以及离散状态和连续动作的在线梯度下降TD（λ）算法，结果表明连续动作的强化学习代理在投资组合分配方面始终表现最佳[8]。后来，越来越多人将强化学习应用在投资组合管理上，包括，Zhengyao Jiang等人提出了一种无模型的强化学习框架，然后在加密货币市场上进行投资组合管理，实验结果表明该框架在50天内能够实现至少4倍的回报[9]；Lili Tang等人提出了一种在不确定环境下基于模型的actor-critic算法，该算法可以得到稳定的投资，收益可以稳定增长[10]；Lin Li等人使用递归强化学习进行直接投资组合选择，该方法能够胜过某些最新的投资组合选择方法[11]；Yuh-Jong Hu等人使用了GRU网络和风险调整后的报酬函数，再利用强化学习解决投资组合的策略优化问题[12]。

然而上述这些研究多数都是使用的国外的数据，对中国股市的研究较少。针对国内股市，涂申昊等人针对投资组合理论中的不足，提出了一系列的模型来改进优化传统的均值方差模型，并引入了深度强化学习模型进行市场择时研究[13]；齐岳等人采用深度强化学习中的DDPG算法，通过限制单只股票的投资权重对中国股市进行投资组合，投资组合价值显著高于平均投资策略[14]；Zhipeng Liang等人实现了三种最先进的连续强化学习算法，结果表明，PG比DDPG和PPO效果更好，尽管后面两者都比PG更先进，并对比了美国股市和中国股市，但在中国股市上强化学习代理看起来似乎没有学习[15]。DDPG效果不如PG的原因可能是DDPG的不稳定性和难收敛性，所以本文决定将更先进的TD3算法应用于投资组合管理问题中来，并在中国股市进行了深入研究。

2 问题描述

投资组合管理的任务是在承担一定风险的条件下，使投资回报率实现最大化，投资经理需要通审时度势来改变各资产类别的权重。例如，若一个投资经理判断在下一时刻某一资产的总体状况相比其他资产而言对投资者更有利的话，则需要将投资组合的权重向该资产转移，这里的投资经理在本文是我们的深度强化学习代理。我们使用股票作为风险资产，使用国债作为无风险资产构成投资组合的资产包。

2.1 MDP定义

股票交易数据是一种常见的金融时间序列，金融时间序列指以时间（分钟或天）为索引的金融数据。本文以天为交易周期，并对股票时间序列进行如下表示：

其中，X表示交易周期为天的股票时间序列，xt表示第t个交易日的特征向量。当以股票原始交易数据作为特征向量时：

强化学习中通常将马尔可夫决策过程（MDP）定义为一个四元组(S,A,R,P)，其中：

（1）S为所有环境状态的集合，在投资组合管理问题中，环境包括市场上所有可用的资产和所有市场参与者对它们的期望。强化学习代理不可能获得如复杂的环境状态的全部信息，Charles等人指出这些所有的信息都可以反映在资产的价格上[16]，另外根据Zhipeng Liang等人在特征组合方面所做的工作[15]，在本文中我们对每一个资产使用作为输入的特征向量。为了简化问题，我们使用在交易日t往前看一个窗口w的方式来表示环境状态stϵS，然后数据预处理的方式是在训练集、验证集、测试集中的每一个窗口内除以收盘价在该集合中的最大值，即：

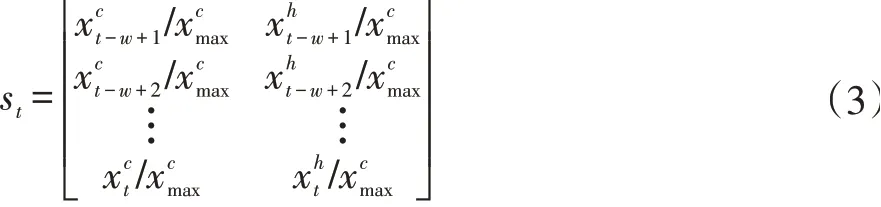
（2）A为强化学习代理可执行动作的集合，本文所使用的资产包一共有6个资产，所以在交易日t的动作为atϵA，即投资组合权重，可以表示如下，

其中，wt,0为国债的持有比例，wt,1到wt,m为每支股票的持有比例，在本文中m=5。

（3）R为奖赏函数，是强化学习代理执行一个回合之后所获得的累积回报，rt是在状态st执行动作后获得的立即回报。在单资产问题中，rt有简单收益率和对数收益率两种，在不考虑交易成本时分别表示为：

简单回报率是计算立即回报的一种更为简单的方法，但它不是一种对称方法，所以这里我们选择对数收益率。

设投资组合价格波动向量为yt：

则立即回报rt为：

累计回报R为：

设初始投资组合价值为p0，则在第t天结束时的投资组合价值pt为：

（4）P为状态转移概率，其中p(st+1|st,at)定义为在状态st下采取动作at转移到状态st+1的概率。我们假设MDP满足p(st+1|st,at,…,s1,a1)=p(st+1|st,at)。由于市场环境复杂，我们无法知道从一个状态转移到另一个状态的概率，但是无模型的强化学习方法利用采样的方法克服了这一缺点。

2.2 交易成本

在真实的股票交易过程中，买和卖都不是免费的，交易费用由印花税、过户费、券商佣金这三部分组成。

由于股票价格变动，投资组合权重会发转移，假设在第t天开始时权重向量为at-1，在一天结束的时候会转变为a't：

其中，⊙表示逐元素相乘。在第t天快结束时，投资经理通过买卖会使a't变为at，在这个交易期间产生交易成本，如图1所示。

图1 投资组合权重转移

图1 中第t天开始时的投资组合价值为pt-1，经过价格波动yt-1在结束时变为p't，然后经过买入和卖出之后在第t+1天开始时变为pt。为了简便起见，设本问题中的交易成本为到pt缩水的比例μt∈[0,1]，所以：

Moody等人指出[17]，当买入的手续费等于卖出的手续费，且均为c时，可以估计交易成本为：

根据（9）式可知，引入交易成本之后的立即回报rt为：

所以引入交易成本之后在第t天结束时的投资组合价值为

2.3 投资组合策略

（1）平均投资策略（Uniform Constant Re-balanced Portfolios），投资组合权重在所有资产中平均分配，在整个交易期间不做任何更改，同时不会产生任何交易成本。

（2）跟随赢家（Follow the Winner），投资组合权重从表现不佳的资产转移到表现出色的资产上。

（3）跟随输家（Follow the Loser），它认为表现不佳的资产在随后会恢复，所以投资组合权重从表现出色的资产转移到表现不佳的资产上。

（4）买入并持有策略（Buy and Hold），表现为在开始时以全部资金买入某一资产，并持有不动，在结束时卖出，期间不产生任何交易成本。

2.4 缺失值处理

股票市场会在周末、节假日或临时进行休市，另外由于突发事件某些股票也会出现停盘现象，所以有必要对取得的股票交易数据进行缺失值处理。一种简单有效的处理方法就是和股票指数进行对齐，缺失数据时开盘价、收盘价、最高价、最低价都等于上一交易日的收盘价，成交量为0，表示今日未开盘。

2.5 市场假设

（1）假设1：每支股票股数可以按投资组合权重的比例来分配资金进行购买，不一定为整数。

（2）假设2：投资组合权重改变时能够以每支股票的收盘价作为成交价格。

（3）假设3：强化学习代理投入的资金微不足道，为市场没有任何影响。

3 深度强化学习

3.1 PG算法

PG算法是一种直接使用逼近器来近似表示和优化策略，最终得到最优策略π的方法。

假设强化学习代理一个回合的状态、动作、回报轨迹为τ：

则可知π在参数为θ情况时τ发生的概率为：

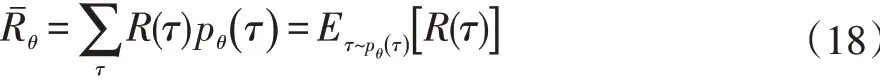
因为：

所以：

具体细节如算法1所示：

算法1：Policy-Gradient

1:Randomly initialize policy parameterπ(a|s,θ)

2:For each episode:

3:Generate an trajectoryτ:{s0,a0,r0,…,sT,aT,rT}，followingπ(∙|∙,θ)

3.2 TD3算法

TD3算法是由DDPG算法改进而来的，主要是为了解决Q值高估的问题，这个问题是由函数近似误差所导致的[18]。

为了更好说明TD3算法，这里我们先对DDPG算法进行简单介绍。DDPG是根据DQN[19]的思路对确定性策略梯度（DPG）[20]进行改进，并基于AC框架提出的一种解决连续动作空间的RL算法。它一共有四个网络：online actor、online critic、target actor、target critic。其中actor用于估计策略，critic用于估计Q值，使用target网络是为了让学习过程变得易于收敛。

更新online critic时是最小化下面的损失函数：

其中，N是批量训练的大小，Qθ为online critic网络，yt为：

其中πφ'为target actor网络，Qθ'为target critic网络。

更新online actor时是利用策略梯度的方法：

其中πφ为online actor网络。

最后使用软更新的方式更新两个target网络：

其中τ是更新率。

TD3相对于DDPG有三个大的改进，用于增加算法的稳定性和性能。第一个是利用Double Q-learning的思想，使用两个独立的critic网络去防止过高估计，但这两个critic网络的估计值总会有高有低，仍然会存在高估的可能，所以经过修剪后的Double Q-learning的目标更新为取两者中的最小值，此时算法有一对on⁃linecritics(Qθ1,Qθ2)和一个online actorπφ：

TD3使用的第三个技巧是目标策略的平滑正则化。确定策略梯度算法中一个担忧的问题是：Q值出现过拟合现象。于是模仿SARSA引入正则化策略用于平滑目标策略，实际是在target actor网络中添加一个小方差的随机噪声，这里的噪声可以看作是一种正则化方式：

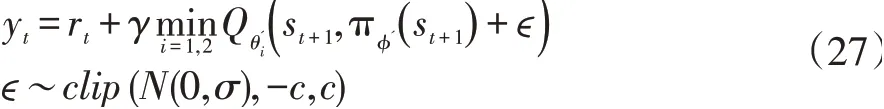
其中ϵ是经过裁剪之后高斯噪声，σ为方差，c为裁剪幅度。

具体细节如算法2所示：

算法2：TD3

1:Initialize critic networksQθ1,Qθ2,and actor net⁃workπφ

2:Initialize target networks

3:Initialize replay buffer B

4:for t=1 to T do

5:Select action with exploration noise+ϵt,,ϵt～N(0,σ)and observe rewardrtand next statest+1

6:Store transition tuple(st,at,rt,st+1)inB

4 实验

4.1 数据集

我们利用中国股市不同行业的龙头企业股票来进行试验，并与hs300指数进行对齐，并尽可能选取较长的数据供强化学习代理进行学习，所以数据集的选取是从2005年4月8日到2019年12月6日。首先去掉历史数据不够长的龙头股票，然后根据2018年12月6日至2019年12月6日最近一年内的成交量总和选取靠前的5支股票，选取出的股票代码如表1所示。成交量越大说明该股票的市场流动性越好，正好满足假设3。数据集共3568个交易日，将其按8:1:1进行划分，选取2005年4月8日至2017年1月16日作为训练集，选取2017年1月17日至2018年6月28日作为验证集，选取2018年6月29日至2019年12月6日作为测试集。

表1 股票代码

4.2 实验结果

（1）学习率

学习率在神经网络的训练过程中起着至关重要的作用。学习率过大时，在训练初期会加速训练过程，使得模型更加接近局部或者全局最优解，但是在训练后期可能会有较大波动，出现模型损失函数围绕最优解徘徊而难以达到最优解的情况；学习率过小时，会导致神经网络的训练非常缓慢，以至于模型在短时间内难以达到最优解。

为了确保我们的神经网络以最优的方式进行训练，在实验过程中我们尝试了不同的学习率，学习率设置如表2所示。

表2 不同算法学习率对比

PG和TD3算法在100回合的Loss变化情况如图2至图5所示。结果显示，学习率对两种算法都会产生显著的影响，较大的学习率会导致它们难以找到最优解，其中TD3算法更加敏感，学习率选择不当可能会导致巨大的波动。

图2 PG算法中策略网络的损失

图3 TD3算法中Actor网络的损失

图4 TD3算法中Critic1网络的损失

图5 TD3算法中Critic2网络的损失

（2）评价指标

投资组合策略的性能可以用多种评价指标来度量，最直观的便是用投资组合价值的年收益率（Annual Percentage Rate）来衡量：

APR的主要缺点是它没有考虑风险因素，夏普比率（Sharp Ratio）[21]是引入经过风险调节后的收益评价指标：其中，rf是无风险利率，这里用国债利率代替。

然而风险衡量的目的是避免巨大的下行风险，因此，惩罚过高的正回报而忽略过高的下行风险的业绩指标是有缺陷的，索提诺比率（Sortino Ratio）[22]提供了一种更好的风险衡量方法：

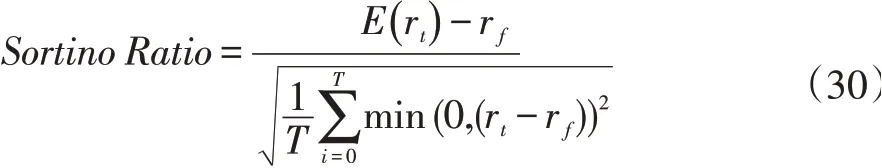
另外一种为了突出下行偏差的衡量方法是最大回撤（Maximum Drawdown）[23]，它是投资组合价值从峰顶到低谷的损失的最大值：

各种策略的性能对比如表3所示，其中PG和TD3与基线的APR对比如图6、7所示。从表3中可以看出，本文采用的深度强化学习方法所获得的APR远高于其他基线方法，其中TD3算法获得84.71%的年利率和PG算法获得的55.06%年利率显著高于基线方法；在其他三个评价指标上，除了MDD以外，深度强化学习的方法也都优于其他方法，且在所有的评价指标上TD3也都优于PG方法。

表3 不同策略的性能对比

图7 TD3算法与基线策略的APR对比

（3）投资组合权重

投资组合管理的目的是分散风险、提高收益，一个好的策略的投资比例应该分散在每一个资产上，而不是将全部的资金都投入某一个资产上。PG和TD3算法在测试集的投资组合权重曲线如图8、9所示，可以看出我们的算法仍不是特别理想，投资组合权重集中在3个资产上，虽分散了风险，但未完全分散。

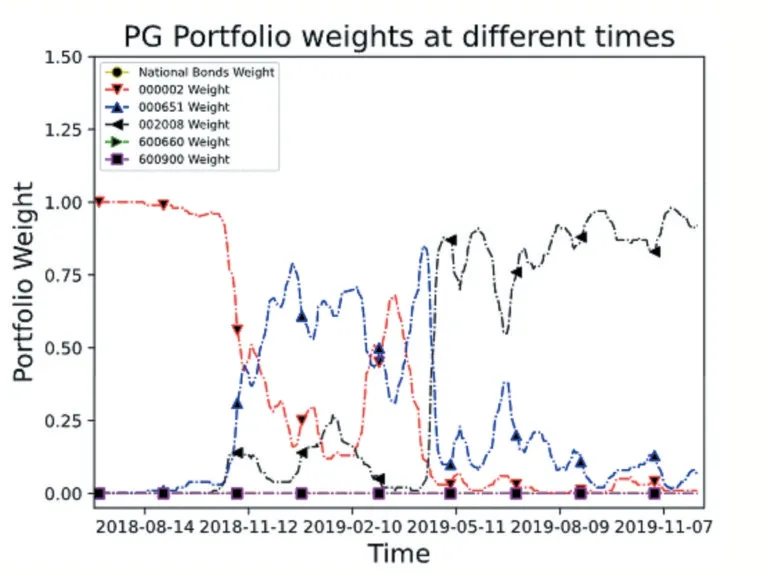
图8 PG算法投资组合权重

图9 TD3算法投资组合权重

5 结语

本文采用了深度强化学习的方法来解决投资组合管理问题，深度强化学习近年来在游戏领域取得的巨大成功也使得深度强化学习蓬勃发展，出现了越来越多的更加有效的新方法。本文在前人基础上，选择了PG和TD3算法对投资组合管理问题进行研究，并取得了显著的成效。

这篇文章通过引入交易成本和对超参数进行调整，虽然取得了不错的效果，但是也存在许多不足有待改进。

第一，从TD3不同学习率的训练过程可以看出，高级的深度强化学习算法的训练过程不是特别稳定，原因与它本身采用target网络的输出作为训练的标签有关，同时也与金融市场复杂的环境有关；

第二，本文采用了前馈神经网络，后面我们将尝试更加复杂的网络结构，诸如LSTM、CNN等；

第三，本文中只利用了简单的对数收益率作为回报，在深度强化学习中，一个好的奖励函数对策略的学习有很大影响，在未来我们会考虑在奖励函数中加入风险因素。

另外在本文的实验过程中，我们发现数据的预处理方式对策略的影响特别大，我们尝试过在窗口内分别除以各个特征第一个值、最后一个值、最大值等方式来进行归一化，但这几种归一化方式都使得我们的投资组合权重容易收敛到买入并持有策略收益率最大的那支股票。本文所使用的在训练集、验证集、测试集分别除以该集合上的最大收盘价的方式来压缩数据有较好的效果，我们猜测可能是前面几种归一化方式改变了原来数据分布，降低了差异，而这些差异可以很好表示金融时间序列的市场波动，不应该被忽略。