一种基于改进仿射投影算法的判决反馈均衡器

杨海斌

（湖南理工职业技术学院，湘潭411004）

0 引言

当前的无线通信技术要求高数据速率和高频谱效率。多输入多输出（MIMO）通信技术可以在不增加任何带宽和功率要求的情况下提供这种通信。然而，在频率选择性MIMO信道中，由于符号间干扰（ISI）和同信道干扰间干扰（CCI）以及噪声的存在，性能会显著下降。需要一个有效的均衡器来跟踪信道变化，来消除ISI和CCI的影响。在文献[1]中已经提出了一些信道均衡方案。其中，判决反馈均衡器（DFE）通常比线性均衡器（MLSE）和最大似然序列估计器（MLSE）具有更好的性能。此外，结合自适应技术和DFE，根据信道条件定期更新滤波权值，可进一步提高系统的性能。

基于最小均方（LMS）[2-3]和递推最小二乘（RLS）的自适应滤波算法是自适应技术中常见的两种算法。LMS算法及其变种计算复杂度较低，但在移动衰落环境中其收敛特性明显恶化，而基于RLS的算法提供了更快的收敛速度，但代价是增加了复杂性[4]。与LMS算法相比，仿射投影算法[5]收敛速度更快，计算复杂度略有增加，但与RLS算法相比，复杂度非常低[6]。

为降低自适应算法的计算量，文献[5]采用了集员滤波方法。该算法可以减少数据更新和迭代次数，以获得相同或较低的稳态误差，但其采用归一化最小均方（NLMS）算法进行最小均方滤波，收敛性能在频率选择信道中大大降低[7]。为此，本文基于数据重用方法，提出了基于集员滤波的仿射投影算法。

1 信号模型

我们考虑一个M×NMIMO系统，其中N和M分别为发射天线和接收天线的个数，信道假设为无线和时变信道，噪声假设为加性高斯白噪声。假定每条发射天线和接收天线间的链路为一个独立的单输入单输出（SISO）信道。所以在第j个接收天线上，k时刻接收信号yj(k)为：

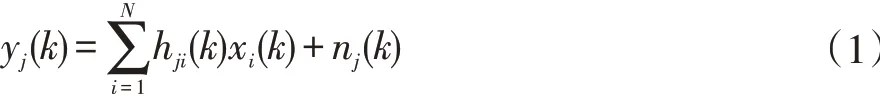
其中i=1,2,…,N，j=1,2,…,M，xi(k)表示第i个发射天线上的发送符号，hji(k)是k时刻第i个发射天线到第j个接收天线的复信道脉冲响应，nj(k)是k时刻第j个接收天线上的加性高斯白噪声。

定义判决装置的第i次输入和输出信号分别为zi(k)和ri(k)，于是zi(k)可表示为：

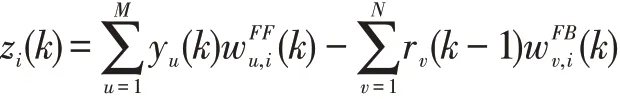
于是zi(k)可重写为：

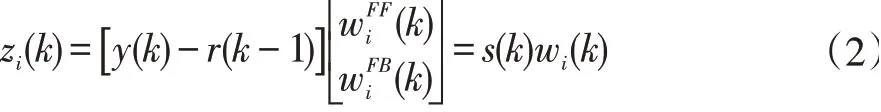
定义误差ei(k)为期望输出di(k)与滤波器输出zi(k)的差，因此有：

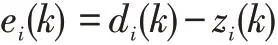
根据文献[4]，可将判决装置的第i次输出信号ri(k)作为系统第i次期望输出信号di(k)。

2 SM-APA算法

本文中，利用基于集员滤波的仿射投影算法（SMAPA）更新判决反馈均衡系统的滤波器系数，在SMAPA中，利用k时刻的前P个输入向量构成N×P维输入矩阵，使得高相关输入信号的收敛速度加快[8]。该算法中只有当参数估计误差大于给定的误差门限时滤波器系数才进行迭代更新，从而减少了滤波器系数的迭代次数。在SM-APA算法中，用约束集H(k)表示k时刻输出误差幅度在门限γ内的所有w的集合，即：

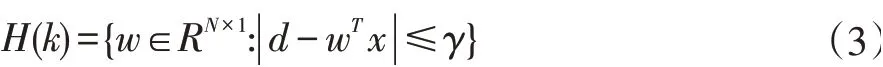
并定义资格集合ψ(k)为H(j)，j=1,2,…,k的交集，算法的目标是当w∉ψ(k)，滤波器权系数才得到更新，ψ(k)可写成：

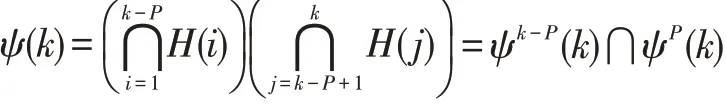
式中ψk-P(k)表示前k-P个约束集的交集，ψP(k)表示后P个约束集的交集。

图1 判决反馈均衡器系统框图

根据最小扰动原理，SM-APA算法目标应使得前后两次更新滤波器系数的欧氏距离最小，即求解以下约束优化问题：

并且受制于约束条件：

式 中Di(k)为P×1维 期 望 输 出 向 量，Di(k)=[di(k)di(k-1)...di(k-P+1)]，S(k)为P×(MLFF+[NLFB)]维输入信号矩阵，即：

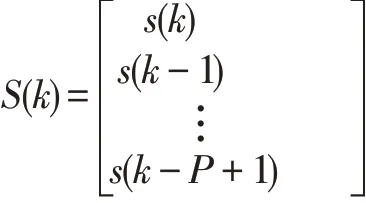
γi(k)为误差门限向量，写成向量形式为：

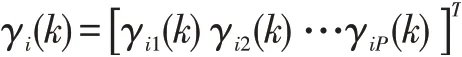
使用拉格朗日乘子方法解决上面的最优化问题，得到：

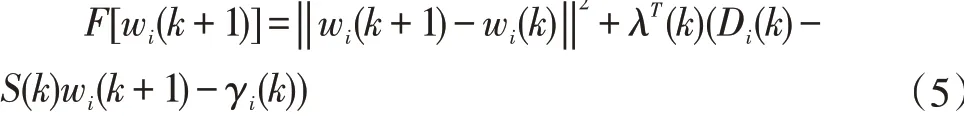
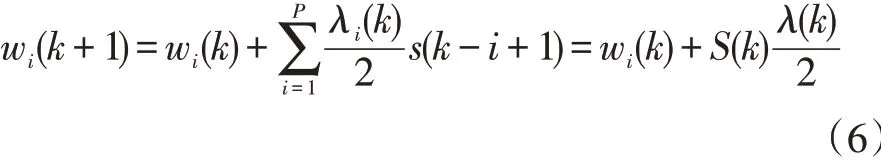
上式两边同乘ST(k)，结合约束条件，有：

于是有：

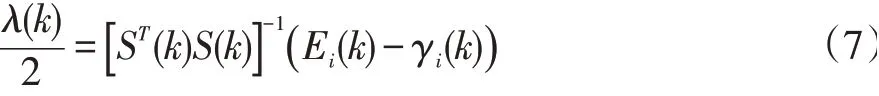
上式中Ei(k)为误差向量，其包含第k次迭代时的先验误差ei(k)和P-1个后验误差：

将式（7）代入式（6），得到SM-APA算法迭代公式为：

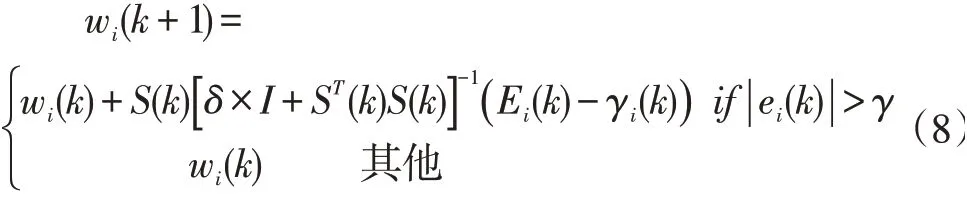
上式中δ为正则化因子，是为防止出现不稳定引入的很小的常数，根据文献[8]，后验误差值εi(k-j)将接近于各自的约束边界值γij(k)，且γi1(k)略小于γ，所以有：

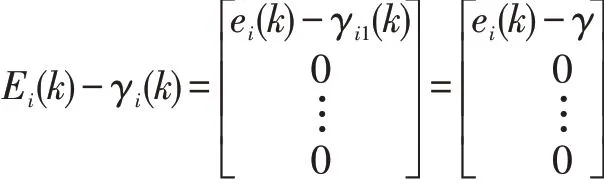
代入式（8），并引入步长参数μ，SM-APA算法迭代公式可重写为：

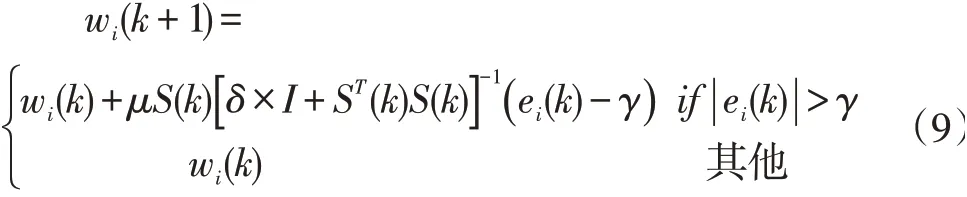
3 仿真

本部分给出了仿真结果，并讨论了基于SM-APA算法的MIMO-DFE的性能。我们考虑了2×2 MIMO信道的自适应DFE方案。采用了QAM调制方案，噪声被认为是加性高斯白噪声。我们考虑每个数据包包含2048位，其中包含256位训练序列。

图2 比较了SM-APA算法和AP算法以及SMNLMS的算法的均方方误差收敛性能。在该仿真中，误差门限设为，其中σn为加性高斯白噪声的方差。采用投影阶数P=3和步长μ=0.05。图2表明，本文所提信道均衡方案比SM-NLMS算法具有更好的收敛性，与基于AP算法的收敛性相当，但因为本文采用数据选择性更新，与基于AP算法的判决反馈均衡相比，减少了计算量。

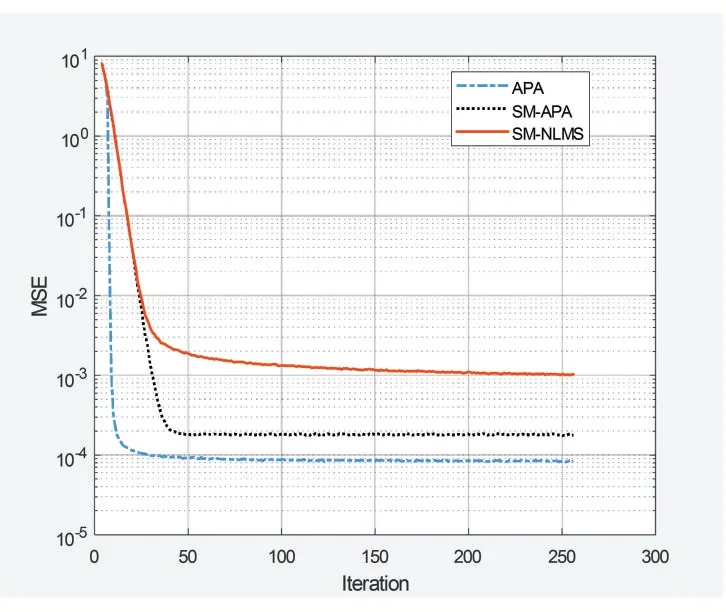
图2 算法均方误差收敛性能比较

图3 比较了不同自适应均衡算法的误码率性能。结果表明，在低信噪比区域，SM-NLMS算法和SMAPA算法具有相似的误码性能，但SM-APA算法在高信噪比区域具有较好的性能。此外，当信噪比小于10db时，SM-APA算法和AP算法的性能非常接近，但在高信噪比情况下本文算法性能更好。

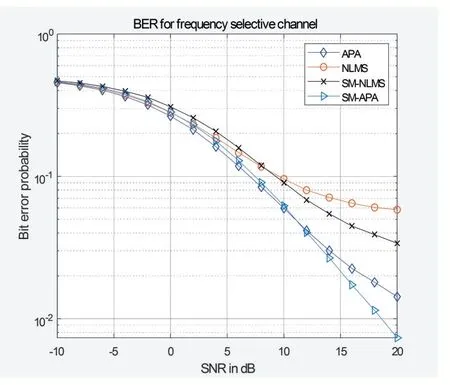
图3 算法误码率性能比较

4 结语

本文研究了采用SM-APA算法的自适应判决反馈均衡器的性能。该均衡方案与基于AP算法的均衡器具有相似的性能，但计算量大大减少。此外，它的性能优于SM-NLMS算法。同时指出误差门限的选择是重要的，它反映了系统的性能和复杂度。