一道极坐标系下交换积分次序题的思考
简彩仁 吕书龙 周勇
(1.厦门大学嘉庚学院,福建漳州 363150;2.福州大学数学与计算机科学学院,福建福州 350116)
引言
极坐标系下交换积分次序在二重积分交换积分次序中有重要的理论地位。许多教材和辅导书都对其进行了研究[1-4].许多考研教辅[2-4]都给出了类似于引例的例题进行分析。
引 例[3]交 换I=的积分次序,其中f(r,θ)连续。
解:r=2acosθ是圆x2+y2=2ax,即(x-a)2+y2=a2,由原积分I可知积分区域D,如图1所示,欲将原积分I化为先θ后r的积分,用r=C(中心在原点的同心圆)穿过积分区域D。
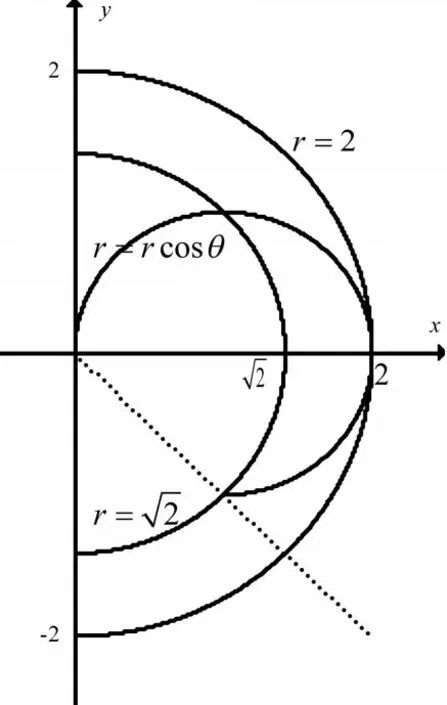
图1
由表3和表4可知,A,B,C均有显著性差异,3个因素对香辣香菇酱感官质量影响的主次顺序为:B>C>A,即黄豆酱>菜籽油>食盐。最优配方为A2B2C2,即每100 g干香菇,加入食盐10 g、黄豆酱80 g、菜籽油200 mL。
该方法的主要特点是后积变量的上下限是常数,但由于部分学生对极坐标相关知识的不熟悉,不能很好地理解该方法。基于对该类问题的研究,并参考直角坐标交换积分次序的思想,文章提出一种适合极坐标系下的二重积分计算方法。文章对极坐标系下二重积分交换积分次序展开讨论,利用积分变量符号无关性,将极坐标系下交换积分次序问题转化为直角坐标系下交换积分次序问题,一方面力求达到数学理论方法的统一美,另一方面也为《高等数学》课程中关于交换积分次序的教学提供参考。
一、理论分析
为叙述方便,不失一般性,将被积函数f(r,θ)r直接记为f(r,θ).本文研究二重积分的交换积分次序。
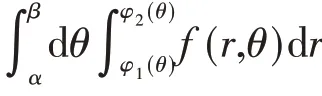
根据积分变量符号无关性,有

假设Y型积分区域{(x,y)|φ1(y)≤x≤φ2(y),α≤y≤β},也可以看成X型区域

根据直角坐标系下交换积分次序的理论,有
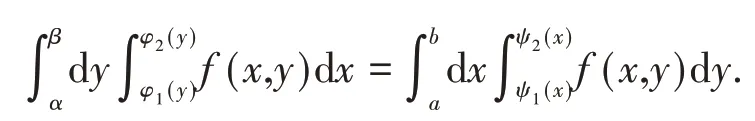
再根据积分变量符号无关性,有
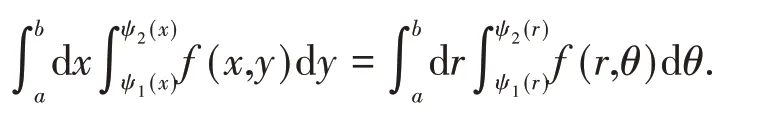
于是得到在极坐标系下交换积分次序的公式为
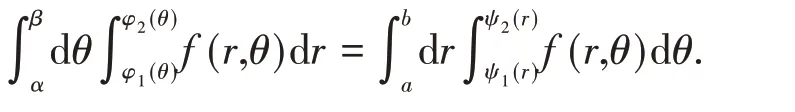
通过以上的理论分析,不难得到在极坐标系下交换积分次序,不必研究极坐标系下交换积分次序的问题,只需将θ和r视为直角坐标系的坐标轴进行积分即可。
基于以上讨论,极坐标系下交换积分次序问题的求解步骤如下:
第一步:将θ和r视为直角坐标系的坐标轴,建立坐标系,并画出积分区域;
第二步:利用直角坐标系下二重积分的定限原理确定先积变量θ的积分限,再确定后积变量r的积分限;
第三步:写出交换积分次序结果

二、引例求解
本节利用本文提出的方法求解引例。
解:将θ和r视为直角坐标系的坐标轴,画出积分区域如图2。
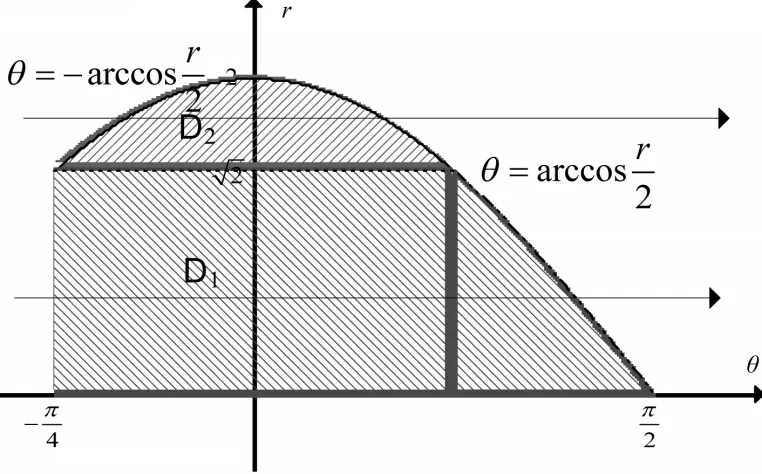
图2
在积分区域D1,先积θ再积r得

在积分区域D2,先积θ再积r得
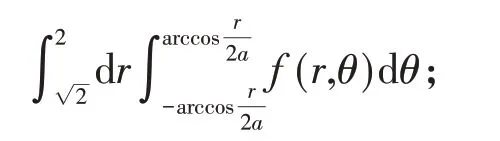
由此,得到交换积分次序的结果为

三、应用
本节通过3个典型的极坐标交换积分次序进行分析。

解:将θ和r视为直角坐标系的坐标轴,画出积分区域如图3。
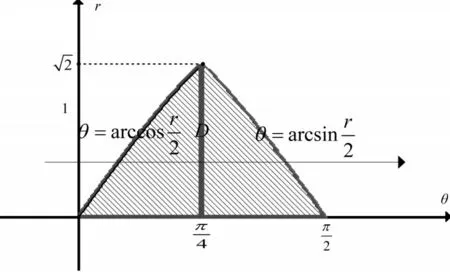
图3
在积分区域D,先积θ再积r得
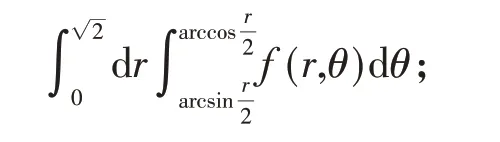
由此,得到交换积分次序的结果为

例2.交换二次积分的次序

解:将θ和r视为直角坐标系的坐标轴,画出积分区域如图4。
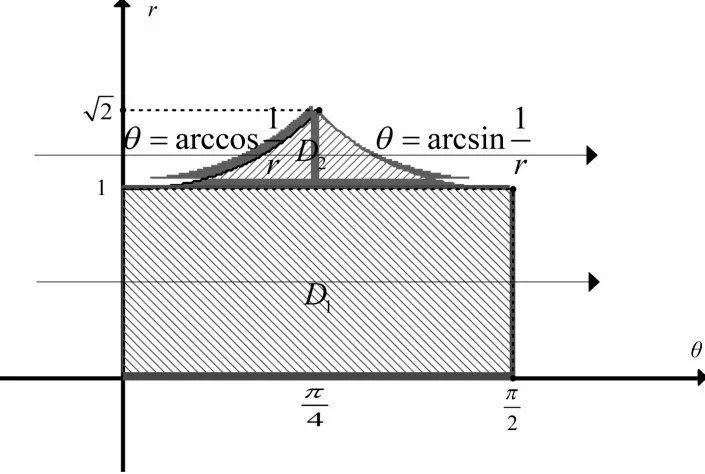
图4
在积分区域D1,先积θ再积r得
在积分区域D2,先积θ再积r得
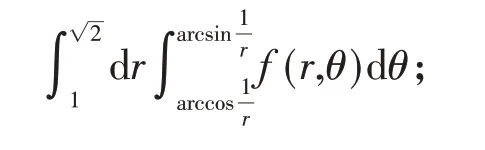
由此,得到交换积分次序的结果为

例3.交换二次积分的次序

解:将θ和r视为直角坐标系的坐标轴,画出积分区域如图5。
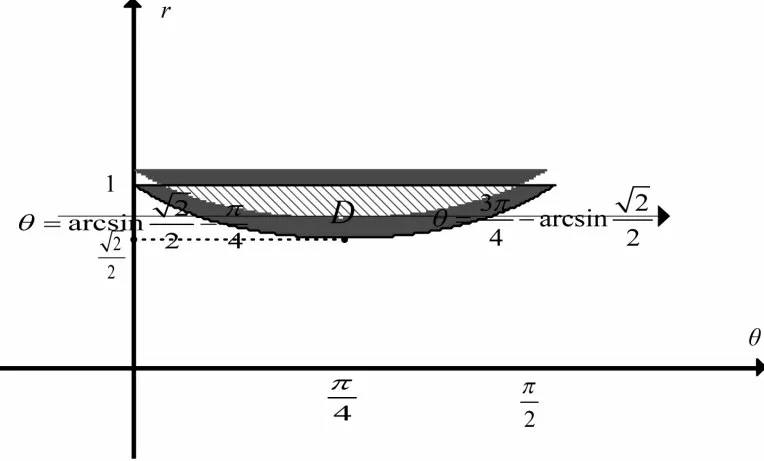
图5
在积分区域D,先积θ再积r得
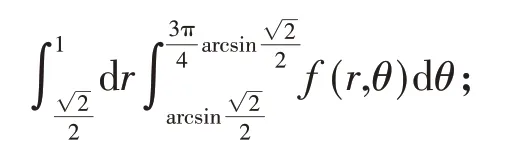
由此,得到交换积分次序的结果为

四、结论
文章研究了极坐标系下二重积分交换次序的问题.从二重积分的积分变量符号无关性得出并不需要在极坐标系下进行交换积分次序,只需将将θ和r视为直角坐标系的坐标轴,直接利用直角坐标系交换积分次序的方法进行研究即可。

