浅谈交换积分次序

苏晓海

（陕西理工学院 数学与计算机科学学院，陕西 汉中 723001）

在任何一次《高等数学》的考试中，都至少必有一道题是关于交换积分次序的，因此掌握交换二重积分的积分次序就显得非常必要。 本文我们通过几个例子来谈一谈如何交换积分次序。

引理 设闭区域D 既是X-型，又是Y-型，即

D=｛（x，y）|a≤x≤b，φ1（x）≤y≤φ2（x）}，或D=｛（x，y）|c≤y≤d，ψ1（y）≤x≤ψ2（y）}，则

公式（1）叫做把二重积分化为先对y 后对x 的累次积分，而公式（1）叫做把二重积分化为先对x 后对y 的累次积分。

所谓的交换二重积分的积分次序就是：如果原来是先对y后对x 的累次积分， 那么把它化为先对x 后对y 的累次积分（如果原来是先对后对的累次积分，那么把它化为先对y 后对x的累次积分）。

大多数同学觉得交换二重积分的积分次序较难， 原因是没有掌握好交换积分次序的主要方法和步骤。 下面我们就以把公式（1）转化为公式（2）来介绍交换二重积分的积分次序的方法：

（1）在坐标面上画出四条曲线x=a，x=b，y=φ1（x），y=φ2（x），它们所围成的闭区域就是积分区域（如图1）。

（2）再把积分区域看成型，即D=｛（x，y）|c≤y≤d，ψ1（y）≤x≤ψ2（y）}。

（3）交换积分次序，得

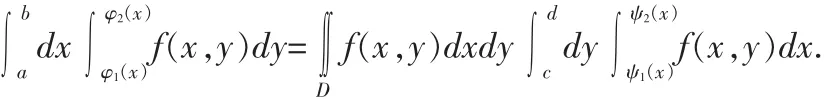
以上三个步骤中，最关键的一步就是（1），很多同学不会交换积分次序其实最大的问题就是弄不清楚积分区域是怎样的区域。 三个步骤中的第一步主要是画四条曲线来确定积分区域，因此我们可以把这种交换积分次序的方法叫“四曲线法”。下面举几个具体例子。

（2）D 是Y-型区域：D={（x，y）|0≤y≤2，y2≤x≤2y}；

（3）交换积分次序，得

图1

这道题由于对x 积分时， 被积函数e-x2的原函数不存在，所以没办法直接计算。 但是，如果先交换一下积分次序，问题就解决了。

解 （1）画四条曲线：y=0，y=1，x=0 和x=2y，得积分区域D1（如图2）；再画四条曲线：y=1，y=3，x=0 和x=3-y，得积分区域D2（如图2 中的阴影部分）；

（2）D=D1∪D2是X-型D={（x，y）|0≤x≤2，≤y≤3-x}；

（3）交换积分次序，得

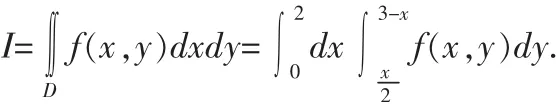
图2

[1]同济大学应用数学系.高等数学（上下册）.第五版.北京：高等教育出版社，2002

[2]王树勋，田壤等.高数学（上下册）.第三版.西北工业大学出版社，2012