交通流多时间尺度特性分析与参数模型研究*

曹 洁，孙兆军，张 红,2，陈作汉,2，侯 亮,2

(1.兰州理工大学 计算机与通信学院,甘肃 兰州 730050;2.甘肃省城市轨道交通智能运营工程研究中心，甘肃 兰州 730050;3.甘肃省制造业信息化工程研究中心，甘肃 兰州 730050)

0 引 言

在智能交通系统中，建立准确稳定的交通流参数模型是实现智能交通诱导与控制的关键[1]。交通流参数模型通常以描述交通流运行特性的三个参数(速度、流量和密度)为基础，考虑到交通流数据统计时间尺度的不同，交通流序列因受到各种复杂因素的影响，表现出较强的非线性和时空特性。因此，分析交通流在不同时间尺度下的特性，揭示交通流特性参量间的相互关系和内在时空演变规律，可为完善交通流理论、进行交通状态识别提供科学依据和理论支撑。

对于交通流时间序列的分析主要有：数理统计方法、机器学习方法、可视图方法以及复杂网络方法[2]。针对交通流参数模型的研究，国外起步较早，从格林希尔治提出的第一个速度—密度关系模型开始，学者基于此模型进行了大量的探索研究。这些研究大体上可分为三类：1)研究基于“车辆跟驰模型”建立Aw-Rascle交通流模型，并对模型的关键参数进行了估计[3,4];2)研究混合、异质交通条件下的交通流模型[5～7];3)研究约束条件下的交通流参数模型[8,9]。这些研究发现，已有的关系模型无法准确表示所有的交通状态，例如交通流在自由流状态和拥挤态下的运行特性以及参数关系均存在较大差异。

本文采用Lempel-Ziv算法计算不同时间尺度下交通流时间序列的复杂度，利用相关性分析方法，探索了交通流在时间和空间上的相关性。并针对现有的单段函数模型无法准确表征不同交通状态下交通流参数关系的问题，提出了一种二阶段交通流参数关系模型。

1 交通流多时间尺度特性分析

1.1 实验数据描述

实验数据来源于美国加州交通局运行监测系统(performance measurement system，PeMS)，选取地点为美国加州洛杉矶市编号为US101-N的高速公路，选取检测站编号为VDS769403,VDS 717484和VDS 769388，数据的时间跨度为2018年7月到10月，实时采集的时间间隔为30 s，经过PeMS系统整合得到时间间隔为5,15,30,60的交通流数据，每个检测站记录了该高速公路4个车道的交通流量、速度和占有率等数据。

1.2 交通流时间序列复杂度计算

本文将Lempel-Ziv算法[10]引入到交通流时间序列复杂度计算中，Lempel-Ziv算法的步骤如下：

Step1 给定一个包含n个元素的时间序列(y1,y2,…,yn)，则可以按照以下规则重构一个符号序列(s1s2…sn)：如果yi>y(其中，y表示时间序列的平均值)，si=1；否则，si=0，因此，序列{s1s2…sn}是一个0-1符号序列。

Step2 定义变量c(n)为符号序列(s1s2…sn)的复杂度，S和Q分别为两个不同的符号序列，SQ表示S,Q两个符号序列相加组成的总符号序列，SQπ表示删去SQ中最后一个字符所得的符号序列，ν(SQπ)定义为SQπ的所有子序列集合。

Step3 初始化c(n)=1,{s1}=1,{s2}=1,S=1和Q=1，因此SQπ={s1}。假设S={s1s2…sr}，Q={sr+1}，若Q∈ν(SQπ)，则符号序列Q是{s1s2…sr}的一个子序列，因此，复杂度值保持不变，只将Q更新为{sr+1sr+2}，再判断Q是否属于ν(SQπ)(符号序列SQπ也被更新)，重复上面的步骤，直到Q∉ν(SQπ)，然后,将c(n)值加1，读取下一个字符并取Q={Sr+3}。

Step4 重复以上步骤，直到符号序列{s1s2…sr}中的所有元素都被计算到，则得到的c(n)是给定时间序列的复杂度。

Step5 根据Lempel-Ziv算法，定义归一复杂测度为

CN(n)=c(n)/b(n)∈[0,1]

(1)

(2)

使用L-Z算法计算不同时间尺度下的交通流时间序列复杂度值。如图1所示，5 min数据的样本总容量为8 640，其CN值在21天后大约在0.210；15 min数据的样本总容量为3 840，其CN值在36天后大约为0.195；30 min数据的样本总容量为2 496，其CN值在42天后大约为0.200；60 min数据的样本总容量为1 440，其CN值在55天后大约为0.190；可见，5 min时间尺度的交通流序列的复杂度高于其他时间尺度的复杂度，对于交通流时间序列，不同时间尺度的交通流数据具有不同的复杂度值。通过以上复杂度计算的分析表明，小时间尺度的数据表现出较为明显地波动性和随机性，其复杂度较大；随着时间尺度变大，数据逐渐平滑，其削弱了随机性、降低了复杂度。

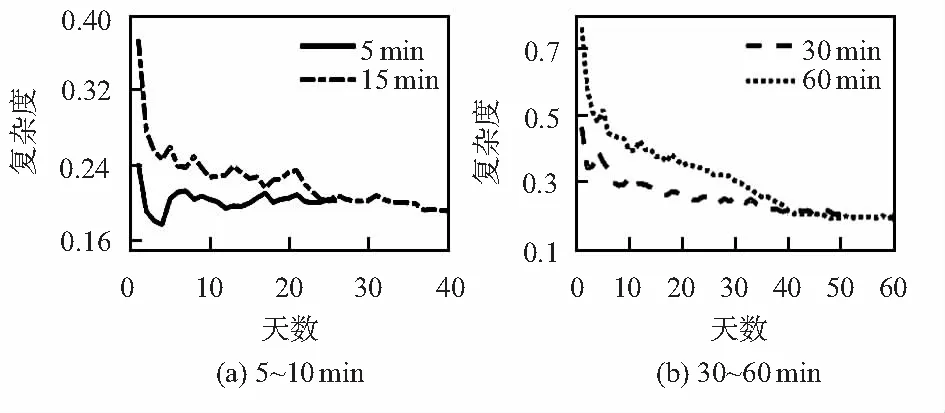
图1 不同时间尺度下的交通流复杂度

1.3 交通流时空特性分析

交通系统是一个相对较封闭的复杂系统，交通流数据是典型的时空大数据，具有不同于其他时间序列的特征。表现在时间上，下一时刻的交通流可以看作是前一时刻数据在特定规律下的延续；表现在空间上，交通流数据受上下游和相邻车道交通状态的影响而呈现出较强的相关性，如某一车道的交通流数据不仅与同一车道上、下游截面的数据有关，还与同一截面不同车道的数据存在相关性。通常用相关性理论中的皮尔逊相关系数(下面简称R系数)来描述交通流的时空相关性，如式(3)所示

(3)

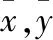
交通流时间序列包括横向时间序列和纵向时间序列,纵向时间序列相关性反映了交通流数据的长期趋势性，通常特定区域内具有较稳定的活动模式和规律性，导致不同周内相同时间的交通流具有较强的相关性。

采用编号VDS 717484检测站连续5个周一5∶00～17∶00的交通数据，时间间隔为15 min,分析交通流的纵向时间相关性，交通流数据趋势图如图2所示。

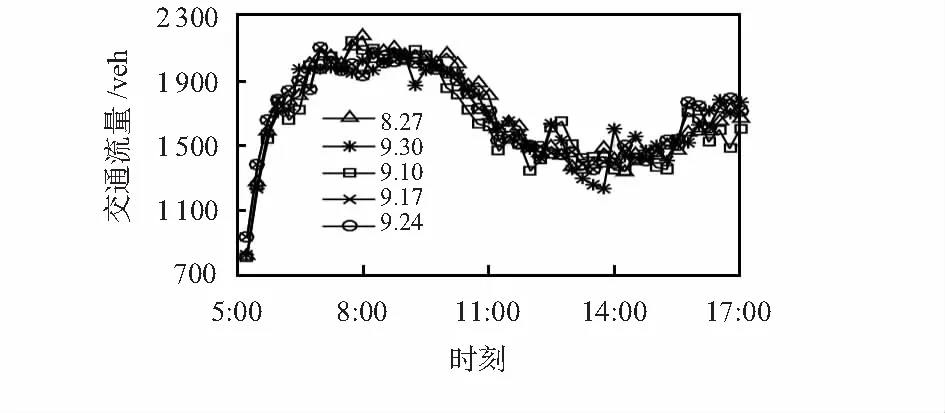
图2 VDS717484检测站连续5个周一交通数据趋势

由图可见，交通流纵向时间序列数据具有较强的相关性，同一时刻不同日期的交通流数据相差不大且时间序列的变化趋势大致一致。为定量描述交通流纵向时间序列数据的相关性，表1给出了连续5个周一交通流数据的相关性矩阵，由表可见，时间序列之间的相关系数均在0.96以上，说明两者之间具有较强的相关性。

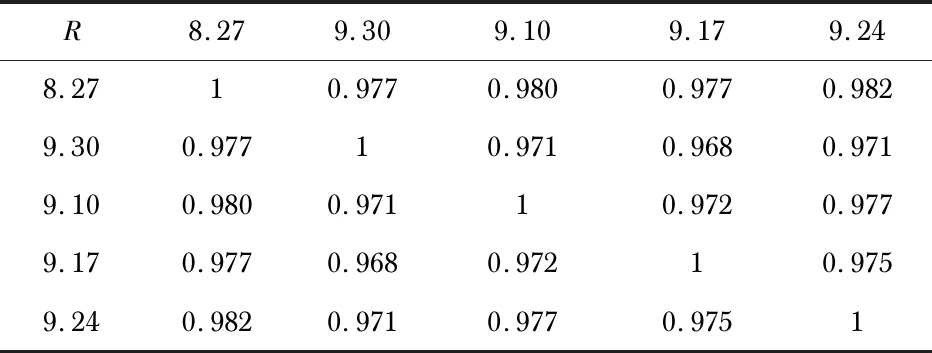
表1 连续5个周一交通流数据的相关性

交通流数据的空间相关性包括横向空间相关性和纵向空间相关性。图3分别给出了同一检测截面不同车道的交通流数据趋势图和同一车道不同检测截面的交通流量趋势图。

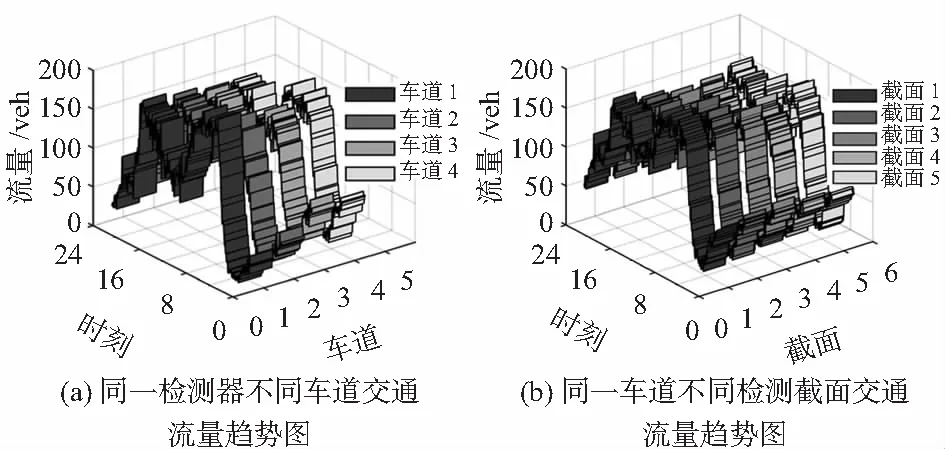
图3 交通流空间趋势

2 交通流参数关系模型

2.1 交通流单段函数模型

典型的交通流参数关系模型主要可分为两类：单段模型和多段模型，单段模型是指使用单一的函数来表示参数之间的关系；而多段模型主要是考虑在不同的交通运行状态下，交通流各参数关系之间表现出不同的函数形式。经典的单段模型主要有：Greenshields模型、Underwood模型、Pipes模型和三参数逻辑(three-parameter logistic,3PL)模型等[11]，其函数表达式如表2所示。

表2 单段函数模型关系式

2.2 二阶段交通流参数模型的建立

单段函数模型结构简单，且与实际的交通流状态存在较大的差异，主要不足有两个方面：1)仅用单一函数形式描述交通流参数之间的整体关系，当交通状态发生转变时，通常不能较准确地表示各状态下的交通流参数关系。2)对于大量交通数据表现出的时间序列趋势特征，单段模型通常显示出无限大的自由流速度和阻塞密度，这与实际的交通情况是不相符的。基于此，本文基于3PL模型提出一种二阶段交通流参数模型，模型的函数表达式如式(4)所示，运用交通流基本参数关系式q=k·v可以推导出速度—密度和流量—速度关系式

(4)

式中vf为自由流速度，kj为阻塞密度，km为临界密度，vm为临界速度。

2.3 二阶段交通流参数模型的拟合

为了验证本文提出的二阶段交通流模型的性能，选择VDS769403、VDS 717484和VDS 769388三个检测站采集到的数据进行模型有效性测试。选取道路各车道流量最大时所对应的密度作为临界密度，则临界密度km依次为30.18，27.80,34.28 veh/km，采用非线性最小二乘法分别对Greenshields模型(GS模型)、Underwood模型(UW模型)、Pipes模型、3PL模型和本文模型拟合流量—密度关系，拟合结果如图4所示。

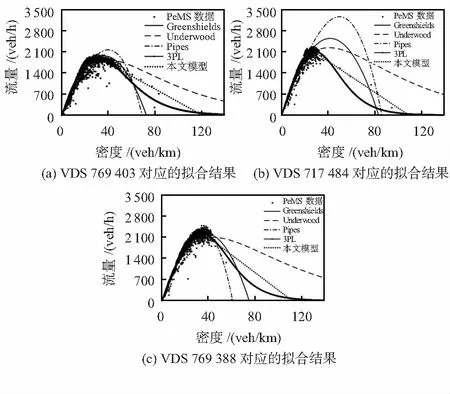
图4 各检测站流量—密度关系拟合结果

2.4 二阶段交通流参数模型性能评价

在模型性能评价时，通常采用相关系数(R2)和标准误差(RMSE)对模型的适用性进行评价，二者的计算公式为

(5)

(6)

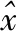
分别使用5种模型对采集的交通流数据进行测试，对于每一个检测站采集的数据，不同的模型产生不同的拟合结果。通过统计分析，图5给出了5种参数模型的相关系数和标准误差对比。模型的标准差越小，表明模型参数标定鲁棒性越高，模型的适用性也越好。由图可见，本文的流量—密度关系模型拟合三个检测站交通数据所对应的R2均最大，分别为0.960,0.976和0.978，标准误差相比3PL模型有所减小，表明本文模型的拟合性能优于其他4种模型。

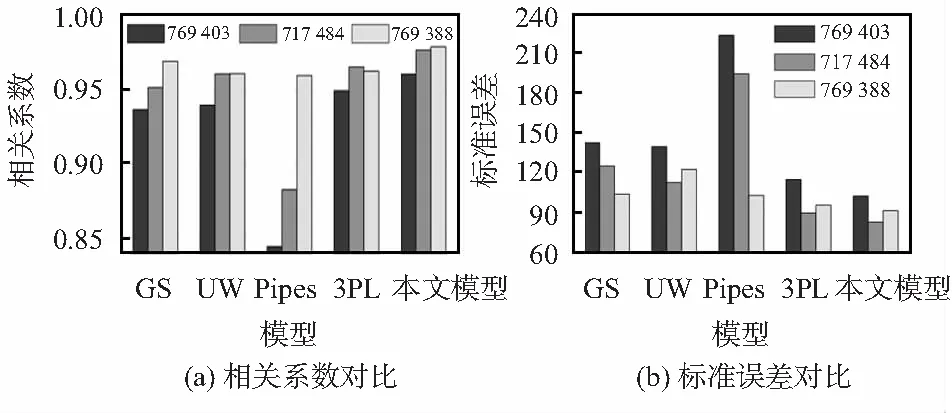
图5 5种模型性能对比

3 结 论

1)采用动力学中的Lempel-Ziv算法计算了不同时间尺度交通流序列的复杂度值，结果表明，小时间尺度的交通流时间序列具有较强的波动性和随机性；在一定的时间序列长度内，其复杂度趋于一个稳定的值。

2)将相关性理论引入到交通流时空特性分析中，采用皮尔逊相关系数计算方法，定量描述了交通流在时间相关性，揭示了交通流序列具有较强的时空相关特性。

3)基于3PL模型提出了一种二阶段交通流参数关系模型。采用非线性最小二乘法，运用5种交通流参数模型对流量—密度关系进行拟合和标定参数，对比发现，本文模型的拟合标准误差最小，表明本文模型可实现对交通流参数关系的准确拟合。

在后续的研究中，需考虑多区域路网的交通流数据进行特性分析，验证模型在不同环境、不同数据集下的适用性和鲁棒性，为交通运行状态分析和短时预测提供理论支撑。