基于环形模板匹配的金属零件识别算法

徐万泽,李柏林,欧 阳,罗剑桥

(西南交通大学 机械工程学院,四川 成都 610031)

0 引 言

模板匹配已经被广泛的应用于图像处理和计算机视觉领域[1]。在金属零件的模板匹配过程中,由于模板图像中一般只包含零件的一个特征面,而在采集到的识别图像中除了包含特征面以外,还会出现零件的不同的侧面,金属零件的其他侧面与特征面具有相似的颜色、加工纹理等特征,使用现有的模板匹配方法并不能很好地解决这类问题,因此需要提出一种新的模板匹配算法。

本文提出了一种利用包含主要纹理特征信息的环形特征模板代替整幅模板的方法,特征在具有旋转不变性与一定尺度不变性的同时,有效地降低了由于匹配图像中包含金属零件不同侧面对匹配准确度带来的干扰。

1 相关研究

模板匹配是指在给出模板图像与目标图像时,通过计算特征相似度,找出目标图像中与模板图像最相似的区域。目前,模板匹配广泛应用于人脸识别、视觉定位、目标追踪、场景识别等领域[2,3]。模板匹配的基本方法可大致分为4类：基于频域和相位的模板匹配、基于灰度值的模板匹配、基于像素梯度的模板匹配、基于局部特征的模板匹配,而现在的研究主要是利用不同特征的融合进行的模板匹配,本文的方法主要采用了像素值、像素梯度和局部特征。

1.1 基于灰度值的模板匹配方法

例如SAD[4],SSD[5]等算法,通过直接计算灰度值之间的一阶或二阶范数,匹配具有较高的精度,但对噪声和光照比较敏感。NCC、MTM[6]等算法,通过利用图像间的互相关性克服了光照的影响,但不适用于局部遮挡的图像。

1.2 基于像素梯度的模板匹配

例如基于形状的模板匹配算法[7],基于广义霍夫曼变换(GHT)的模板匹配算法,基于局部区域的模板匹配算法GLOH[8]等。通过计算像素梯度,可以找到梯度方向相同的成对特征点,可以很好地克服光照变化、局部遮挡和污染对匹配特征带来的影响。但这些方法对于由运动引起的边缘模糊、相机引起的聚焦模糊鲁棒性效果欠佳,几乎不具备尺度不变性和旋转不变性。

1.3 基于局部特征的模板匹配

例如具有尺度不变性的特征匹配算法SIFT[9]以及加速版的SIFT算法SURF等,采用高斯金字塔差分等方法改变图像空间尺度,使匹配特征具有尺度不变性,通过计算梯度主方向对局部图像块进行方向校正,使匹配特征具有旋转不变性。这类算法通常比其他算法有更优越的表现,是目前图像处理领域与计算机视觉领域主要使用的方法。但是它们的性能在很大程度上取决于提取的局部特征的质量和稳定性。如果没有足够的感兴趣点,如在简单的曲线图像中,此类方法的匹配效果将大大降低。

大多数的模板匹配算法都是针对特定的问题,而对于目标自身存在方向变化且同时具有尺度变化和旋转变化的问题研究较少。在自然场景下,往往会同时面临各种复杂的干扰和不同的变化,如在金属零件生产线上,图像采集时零件摆放的位置和方向不同使匹配图像中存在零件的不同侧面,同时还会产生零件的尺度和旋转的变换,因此需要提出一种能在目标自身存在方向变换时,同时具有尺度不变性和旋转不变性的模板匹配方法。

2 金属零件环形模板匹配方法RTMM

2.1 环形特征区域分割

为了解决目标自身存在方向变化对模板匹配带来的干扰,本文将特征面分割成几个环形区域,取包含最多纹理特征的圆环区域代替特征面,以避免目标图像中不同侧面带来的影响。对于模板图像T(x,y),首先将模板分为几个同心圆区域,从同心圆区域提取特征。

第一步：通过双线性插值,改变模板图像T的大小,改变尺度变化比例为Si,图像为Ti,i=∈(1,2,…,N)。

如果T(x,y)的大小为WT×HT,则尺寸改变后的Ti(x,y)的大小为

(1)

第二步：如图1(A)所示,以图像中心为圆心,将图像划分为若干个同心圆区域,在尺度变化比例为Si的模板图像Ti(x,y)内的最大圆半径为Rmax=min(WTi,HTi)。圆形区域划分步长为d

Ri+1=Ri+d

(2)

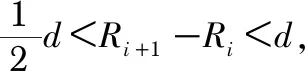
2.2 预选区域筛选特征

在模板匹配过程中,为了减少计算量和加快算法的整体运算速度,首先使用简单特征从目标图像中预筛选出几个预选区域,再进行精确筛选。本文直接采用了每个圆环区域中各自的平均像素大小作为预选特征,如图1(B)所示为有三个圆环区域时的预选区域筛选特征。

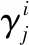
2.3 精确匹配特征

在ARRCH算法中[10],仅采用图像像素梯度方向作为匹配特征,就很好体现了目标图像中的边缘和纹理特征,因此本文也采用像素梯度方向作为精选匹配特征。

1)像素梯度幅值与方向

根据特征关联算子Sobel近似计算像素梯度幅值与方向。若原图为A,Gx及Gy分别代表横向及纵向像素差分,计算公式如下

(3)

图像中每个像素点的梯度近似幅值G与梯度近似方向θ可用以下公式来计算

(4)

2)方向矫正

如图1(C)所示,在尺度变化比例为Si的模板图像Ti(x,y)上,计算梯度平均方向βi作为图像的主方向。

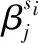
(5)

3)确定环形特征区域

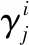
稳定点的提取分为三步：

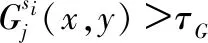
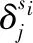
(6)

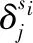
第三步,当同时满足第一步、第二步条件时确定为稳定点Wi。

如图1(D)所示,取稳定点最多的圆环特征区域作为Ti(x,y)上的特征圆环γi,用环形区域图像γi代替整幅模板图像作为模板。

4)特征提取

图1 算法部分中间结果

2.4 由粗到精的匹配策略

根据2.2节中的预选区域筛选特征和2.3节中的精确匹配特征,本文设计了一种先采用预选区域筛选特征进行粗定位,再使用精确匹配特征进行精确筛选的由粗到精的匹配策略。如图2所示。

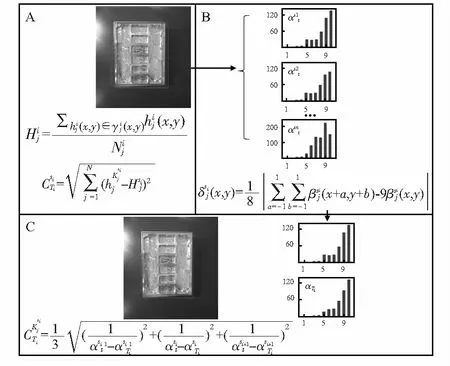
图2 由粗到精的匹配

1)预选区域筛选

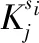
2)精确匹配

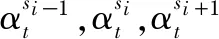
(7)

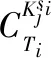
3 实验对比

为了评估算法的效果,给出一种评估方法用于衡量算法的准确值AC

(8)

式中AC为匹配准确值,OT为理想模板的中心位置,Ot为匹配区域的中心位置,D为模板的对角线长。从公式可以看出,OT与Ot位置越接近准确率越高。

3.1 数据集

从生产线上采集了10种不同种类的零件,在模板图像中,只包含零件的顶面,作为模板的特征面。在测试图像中,图像除了特征面外,还包含了一到两个完全不同的侧面,每种零件采集了4张测试图像。另外,为了评估算法在尺度变化和旋转变换下的性能,每张测试图像又进行了相应的变换,扩展测试集(i)图像尺度Si变换由0.5-1.75,变换步长为0.25,共产生200张不同尺寸的图像。测试集(ii)旋转变换由60°-300°,变换角度步长为60°,共产生200张不同角度的图像。测试集(iii)图像同时具有尺度变化与旋转变换,尺度Si变换由0.1-0.5,变换步长为0.1,旋转变换由60°-300°,变换角度步长为60°,两种变换对应融合,例如当尺度Si为0.1时旋转变换为60°,共产生200张不同尺度和不同旋转角度的图像。

3.2 算法参数实验

预设最小同心圆半径为60,步长d由10到50,每次增加5。对于同心圆的步长d,当d过大时,同心圆区域较小,在预选区域时得到的特征维度较低,很容易出现预选区域定位偏差较大,从而降低了算法的AC值。而当d非常小时,精确匹配环形区域中所包含的特征较少,往往会导致错误的匹配结果,也会降低AC值。为了保证匹配的准确值AC,并使环形特征区域尽量包含多的特征信息,综合实验结果图3所示,本文采用的步长d=30。

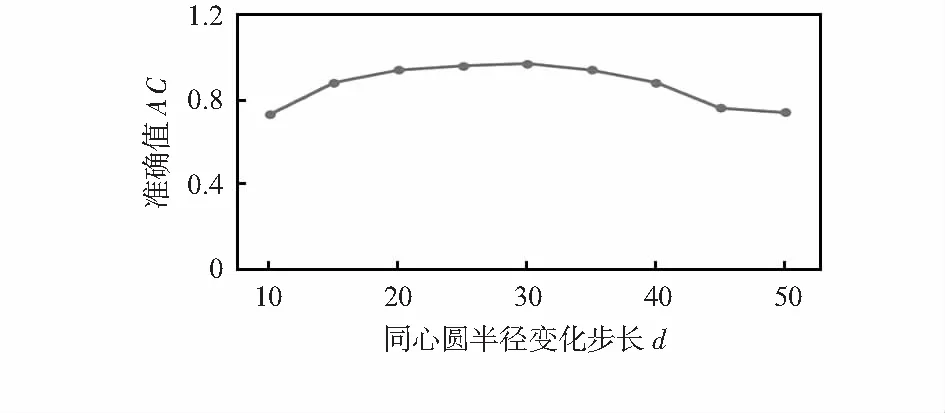
图3 不同步长对准确值的影响

3.3 性能评估

本文选用了几个常用的传统模板匹配算法,通过实验将本文算法RTMM与NCC、SSD、SIFT、SURF进行了比较,在数据集(i)上验证了尺度变换对准确值AC的影响；在数据集(ii)上验证了旋转变换对准确值AC的影响；在数据集(iii)上验证了同时存在尺度变换和旋转变换时,对准确值AC的影响。

尺度变换、旋转变换、尺度与旋转变换的平均准确值AC如图4所示。

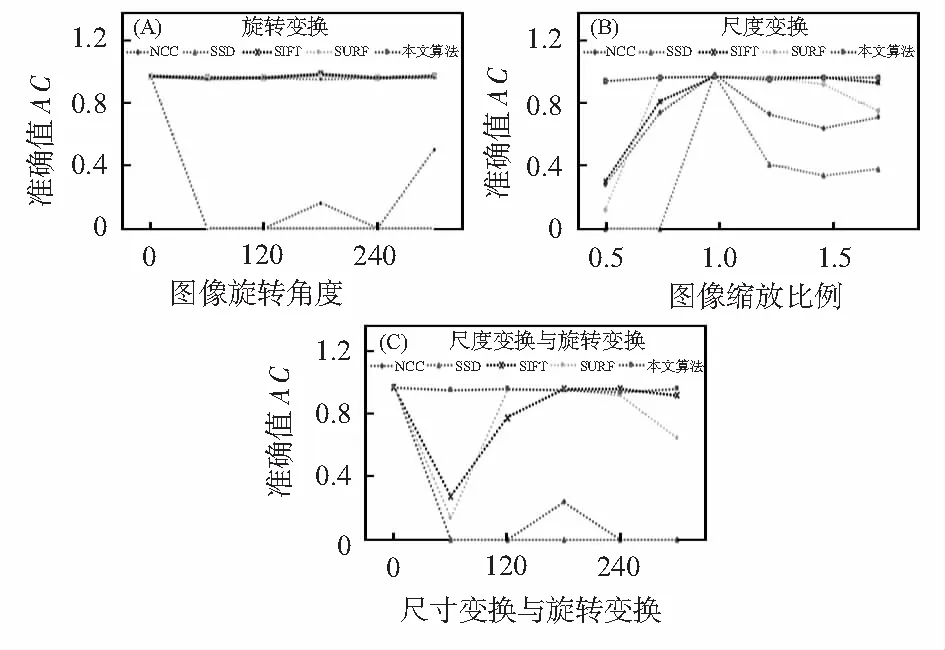
图4 对比试验

观察图4(A)可以得出,在针对图像的旋转变换时,SIFT、SURF和本文算法有不错的表现,它们的准确率非常接近,均大于0.9。观察图4(B)可得出,当尺度缩放比例大于1时,SIFT与本文算法均有不错的表现,SURF在尺度变换超过一定范围后,准确值AC迅速降底,而在尺度缩放比例小于0.75时,本文算法明显优于其他几种算法。观察图4(C)可以得出,在同时存在尺度变换与旋转变换时,相较于其他算法,本文算法的准确值具有非常高的稳定性且高于其他算法。

4 结 论

本文针对模板匹配中目标自身存在方向变化的问题,提出了一种模板匹配方法RTMM,与现有方法相比在尺度不变和旋转不变方面具有更好的表现。但由于算法的预选区域特征使用的是灰度值特征,在非线性光照下算法的准确值有所降低,如在金属零件检测中,由于金属具有强反光性,对图像采集时相机的布置、光照强度和光照方向都有很高的要求。