基于非负矩阵分解与项目热度的协同过滤推荐算法*

杨海清,吴 浩,曾俊飞

(浙江工业大学 信息工程学院,浙江 杭州 310023)

0 引 言

随着Web 3.0的社交平台的快速发展，进行网络信息的获取也就变得十分方便。但大量信息的产生也严重干扰了用户对有关重要信息的获取，个性化推荐技术因此而产生。个性化推荐技术有助于缓解信息过载[1]带来的的负面影响。协同过滤[2](collaborative filtering,CF)是推荐系统中一种常用的技术。近年来，矩阵分解模型[3]因为能够有效地解决了数据的高维稀疏性的问题而受到大范围的推广。通过大量实验证明，在推荐算法中，采用矩阵分解在推荐精度等方面显著高于一些传统的基于邻域的协同过滤模型[4]。针对个性化推荐过程中存在的数据的高维稀疏性问题，文献[5]提出将Slope one算法与用户间相似度相结合进行评分预测，有效缓解了数据稀疏性问题。文献[6]将稀疏边缘降噪自动编码与矩阵分解相结合的混合推荐算法，提高了推荐精度。文献[7]将用户和项目偏置信息融入到非负矩阵分解中。文献[8]将非负矩阵分解模型应用在传统的贝叶斯概率矩阵分解模型之中，使得算法具有良好的可解释性。

传统的基于邻域的协同过滤算法只将相似度作为影响推荐结果的唯一因素，但是在实际场景中，用户进行决策行为时，不只是把性质类似的项目考虑在内，同时项目的热度也会潜移默化地影响用户的实际选择，所以项目热度也是推荐算法的重要因素之一。针对上述问题，本文提出了非负矩阵分解与项目热度进行融合的NMF-IHCF(algorithm of collaborative filtering basedon non-negative matrix factorization and item heat)算法。最后，在MovieLens对本文提出的NMF-IHCF算法进行验证，该算法有效提升了推荐精度。

1 两阶段近邻选择

利用非负矩阵分解得到项目的非负特征空间，采用Pearson系数在项目的非负特征空间上计算相似度，获得第一阶段项目的邻居集，在此基础上引入项目热度概念，结合第一阶段得到的相似度获得融合的相似度，在第二阶段进行邻居选择，最终完成评分预测。

1.1 寻找第一阶段项目邻居群

因为原始用户—项目评分矩阵非常稀疏，很多项目都没有共同的评分用户，导致项目间相似度无法计算。这里，在非负矩阵分解后得到的项目隐式特征空间上计算项目间的相似度，一定程度上缓解了数据高维稀疏性导致相似度计算缺乏准确性的问题。

对于NMF算法，文献[9]采用时间复杂度较低的非负矩阵分解，分解得到用户隐式特征向量空间pu,k和项目隐式特征空间qk,i。文献[10]为了避免矩阵分解过拟合加入正则项。公式如下

(1)

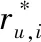
本文采用式(1)得到的项目隐式特征空间，并在项目隐式空间上利用Pearson系数进行相似度计算，同时获得项目的邻居集。记录项目获得评分操作的总次数和项目在k近邻选择时同时充当别的项目邻居的次数。

1.2 第二阶段近邻选择

传统的基于近邻的协同过滤推荐算法往往没有综合考虑项目间相似度和项目热度这两个因素，而在实际过程中，热门商品对用户购买行为的影响也是一个重要因素。NMF-IHCF算法将相似度和项目热度融入到模型之中。

一个项目在全部项目的热度有两部分组成，包括这个项目获得评分操作的总次数和项目在第一阶段k近邻选择时同时充当别的项目邻居的次数。

一个项目获得评分的次数越多，则这个项目越受欢迎，它的评分也越可靠，同样，一个项目越多充当其他项目的邻居则说明这个项目越热门。

这里，用Ti表示单个项目在全部项目中的热度，0≤Ti≤1，如下式所示

(2)

式中fi为项目被用户评价的总次数;qi为在第一阶段k近邻选择时项目同时充当别的项目邻居的次数。

这里，得到融合项目热度的相似度

(3)

式中Tb为项目b在全部项目中的热度;simpear为第一阶段项目隐式空间上得到的相似度。

1.3 预测评分

使用项目热度结合相似度得到的融合相似度，得到第二阶段邻居群。对评分进行预测

(4)

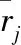
2 算法流程

算法：NMF-IRCF算法

输入：评分矩阵R

输出：预测矩阵Rpred

1)使用NMF分解得到降维后的项目特征空间;

2)在项目的非负低维隐式空间中使用Pearson系数进行相似度计算;

3)根据k近邻算法，寻找邻居集，得出每个项目同时充当别的项目邻居的次数和项目被用户评价的总次数;

4)依据式(2)计算项目热度，再将项目热度结合项目相似度得到融合相似度;

5)根据k近邻算法，再次寻找项目邻居群;

6)利用式(4)进行评分预测。

算法结束

NMM-IHCF算法利用NMF对评分矩阵进行分解不出现负值的特性在推荐算法中的现实意义。同时，在NMF分解后的数据密度提升的低维空间下进行相似度计算，避免了在数据高维稀疏性的情形下计算相似度，然后将项目的热度融入到相似度运算过程，不仅考虑项目热度，同时还能避免传统协同过滤算法仅仅考虑相似度这单一因素的影响，算法的鲁棒性更佳，最终提高了推荐的精度。

3 实验结果分析

为了验证本文提出算法，使用MovieLens数据集进行验证。

3.1 相似度和热度的分布

表1为项目间相似度和热度这两个影响因素的分布情况，显示了影响最终预测结果的两个因素。通过实验得出，当邻居数量参数为20时：相似度主要分布在[0,0.4]，其中相似度在[0,0.2]占所有相似度的46 %。而热度主要分布在[0.4,0.8]，其中[0.6,0.8]占所有热度的39 %。可以看出相似度与热度这两个因素分布情况差别很大。

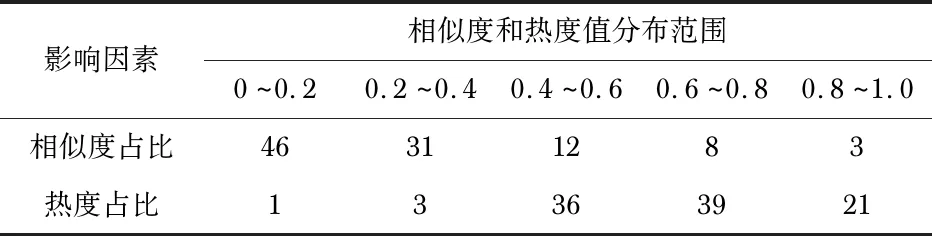
表1 相似度和热度值分布 %

在推荐系统中,每个项目都应该有一个热度指标，符合现实世界中热门商品被热卖的现象。每个项目具有多个相似的邻居项目，可协助对未知评分项目实现评分的合理预测。因此，相似度和热度是两个完全不同的两个因素，把项目的热度概念引入协同过滤推荐算法是可行的。

3.2 实验结果与分析

本文将所提出的NMF-IHCF算法与基于项目的协同过滤ICF算法和基于NMF的协同过滤NMF-CF算法进行对比，使用RMSE作为推荐性能的衡量指标，如图1所示。

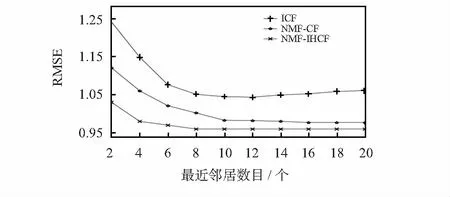
图1 不同推荐策略下的RMSE

本文提出的NMF-IHCF算法在邻居数量低于8时，均方根误差值不断降低；当邻居数量超过8之后，均方根误差的值趋于稳定。而ICF算法随邻居数量的不断提高，均方根误差在邻居数目超过12个之后有略微的反弹，证明邻居数量影响了评分的预测结果。NMF-IHCF算法和NMF-CF算法相比，RMSE更低，说明引入项目热度这一因素确实提高了推荐算法的性能。图1说明本文提出的算法是有效可行的，具有更好的鲁棒性，利用项目热度这一因素优化了协同过滤算法的性能。

4 结束语

本文提出了将非负矩阵分解和项目热度相结合的协同过滤推荐算法。算法不仅考虑到项目间的相似度，同时考虑到项目热度这一因素，最终达到了对推荐精度的提高。该算法弥补了SVD出现负值的影响，并且增强了算法的鲁棒性，提高了算法的预测精度。在接下来的研究重心将放在对非负特征空间下得到的相似度进行约束，获得更准确的相似度，来提高算法的性能。