改进B样条曲线的机器人轨迹拟合研究*

王晓明，宋 吉，郑继新，庞浩帅

(兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050)

0 引 言

目前所研究的机械臂运动轨迹分为两个部分：第一个称为路径规划，规划需要人工根据作业任务和环境设定机器人的工作路径，示教记录之后机器人重复执行规划的路径。但是示教再现无法根据环境因素实时规划出机器人路径。另一个称为轨迹规划，轨迹规划加入时间序列信息对机器人的速度和加速度进行规划，以满足光滑性以及速度可控性等要求，控制各关节在相同时间内运动综合作用到末端执行器，使执行器按工作要求最优执行任务[1]。

1 关节空间轨迹规划方法

关节空间轨迹规划对运动路径的描述是将关节变量表示为时间的函数，对关节空间中如何利用受控参数规划机器人的运动进行研究。设置路径点处的位置和姿态参数，转化为对各关节角度的控制要求，不必考虑笛卡尔空间中两路径点间轨迹的形状[2]。得到的关节轨迹在满足不同的约束条件下，可釆用不同类型的插值运算来实现轨迹规划[3]。对于得到的关节轨迹函数都要求关节变量在极值范围内，各关节位移、速度、加速度和各关节角的插值点处连续，使机器人各关节运动平稳，减小振动，提高工作质量，延长使用寿命[4]。B样条曲线具有很强的局部支撑性、关节角位移变化率较小等优点并且可以多次扩张，不存在瞬时变化等问题。假如需要对规划好的某个关节的某一段轨迹需要调整，只调整B样条曲线所控制的这段轨迹的一个控制点即可，不需要对整个关节轨迹作调整，在很大程度上降低了后续遗传算法寻优的难度[5]。

2 B样条曲线误差对比分析

为了进一步说明改进的三次B样条曲线拟合算法所取得的效果，针对同一序列的型值点，分别用传统的B样条曲线插值算法、拟合算法和改进后的B样条曲线拟合算法实现这些型值点的处理[6]。以抛物线y=(x-4)2为例，在[0,8]区间上均匀生成9个原始型值点。三种方法处理误差结果分别为0.083,0.178,0.042，可以看出改进B样条拟合曲线误差较低。

3 关节参数与轨迹函数计算

为了进一步说明改进的三次B样条曲线对机器人轨迹进行规划的可行性，以PUMA 560工业机器人为研究对象，在机器人关节空间中利用改进的三次B样条曲线对机器人各个关节进行轨迹规划。设初始角加速度为0.2°/s2。仿真过程中所运用的机器人关节点信息如表1所示。

表1 各关节角度值 (°)

根据改进的三次B样条曲线，利用MATLAB软件样条工具箱中相关函数进行编程，对给定的各个关节角度进行拟合得到机器人运动轨迹[7]。假设路径点之间的时间间隔为4 s，得到各个关节轨迹函数，θi(t)表示第i个关节的轨迹，将其前三个关节表示为分段多项式的形式如下

(1)

(2)

(3)

基于以上计算知，在MATLAB软件中利用改进的三次B样条曲线进行机器人关节轨迹规划的推导以及计算是可行的，规划出的各段轨迹函数均可以用三次多项式的形式表示，在各个插值点处轨迹均连续。B样条曲线规划出的轨迹既能满足机器人关节运动轨迹连续平滑、末端执行器运动平稳的要求，又能够快速准确的完成轨迹规划。

4 机械臂末端轨迹仿真

要想在关节空间中规划各个关节的运动轨迹，应先在笛卡尔空间中进行机器人路径点的规划，然后通过机器人逆运动学求解各个关节节点的信息[8]，各个关节依次形成各自的运动轨迹，最终再将各个关节轨迹综合投射到笛卡尔空间中就得到了机器人末端的运行轨迹[9]。再者，机器人不但要达到预定的目标点外，还要在预定轨迹的一定约束范围内运动。因此机器人末端轨迹的建立是关键的一步。在MATLAB软件的Robotics Toolbox工具箱[5]中进行PUMA 560机器人建模。如图1所示。

图1 PUMA 560机器人模型

通过在MATLAB软件中编写程序做出了从起点P0=[0.078 -0.138 0.345]到终点P1=[-0.075 -0.144 0.308]的笛卡尔空间轨迹曲线如图2所示。

图2 末端执行器运动轨迹

5 机械臂关节轨迹仿真

利用上一节所建立的机器人模型，运用改进后的三次B样条曲线进行关节空间中机器人关节插值编程，编写MATLAB程序采用改进后的三次B样条函数拟合的方法可以得到机器人运动过程中各关节位置、速度和加速度的曲线图。机器人6个关节的仿真分别如图3所示。

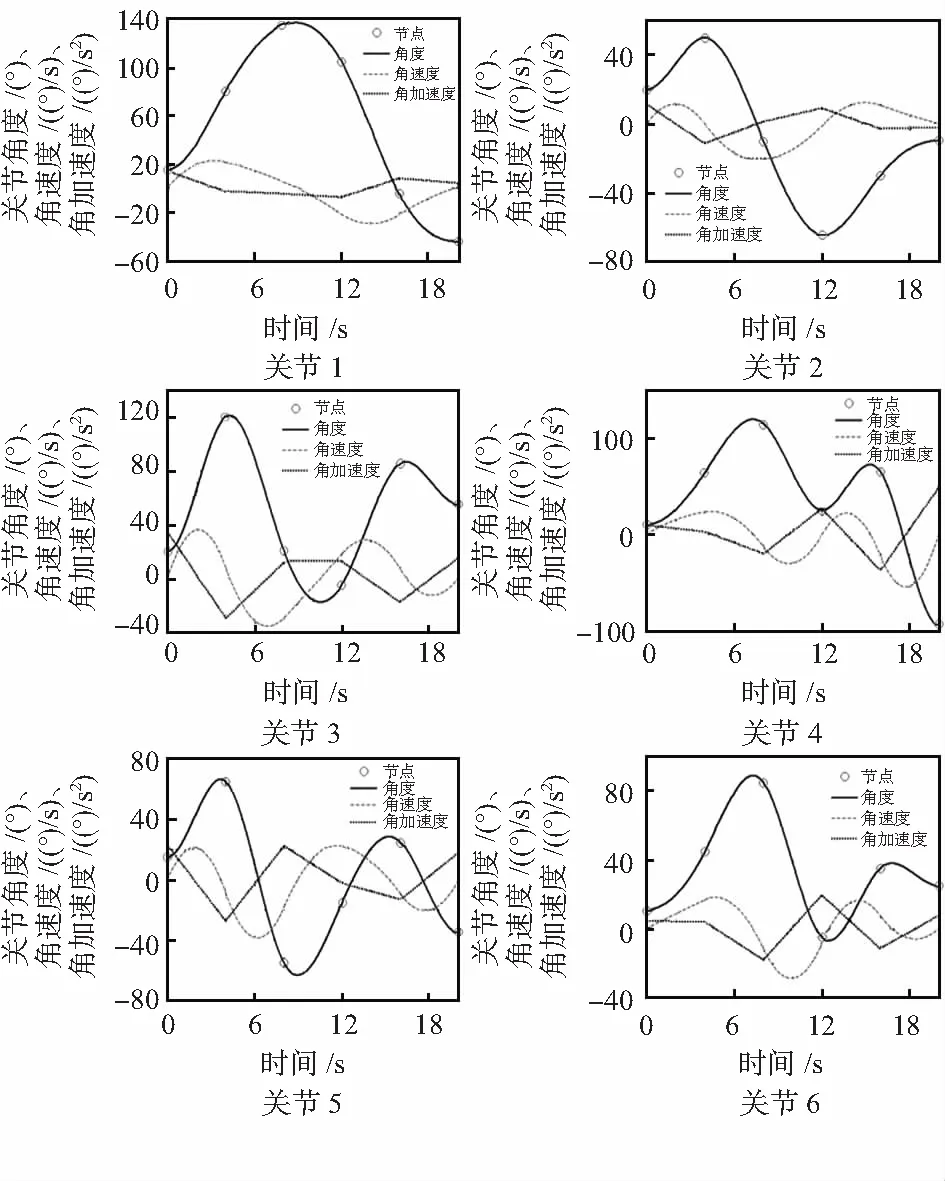
图3 6个关节位移、速度和加速度变化曲线

图3每个关节中的三条曲线可以看出，在机器人整个运动过程中，各关节速度、加速度和加加速度均满足运动学约束条件，各关节角位移曲线连续平稳，同时具有较好的光滑性，几乎没有波动。各关节的角速度连续平滑且无突变，角加速度连续。机器人关节位移变化率较小不会产生抖动现象，所以运动过程平稳无大的冲击和振动，使关节处零部件间的磨损降低，延长了机器人的使用寿命，经过改进的三次B样条曲线规划的机器人关节轨迹均经过了中间轨迹点，有效地提高了三次B样条曲线的拟合精度，从而提高了机器人运行的精度，保证了机器人在实际应用场合的高精度性。

6 结 论

对机器人关节空间轨迹规划的多种方法进行了比较，重点对三次B样条曲线规划算法进行改进，并成功地将其运用到了机器人轨迹规划研究上，提高了机器人运动的精度。最后在MATLAB软件中建立了机器人模型，并对其进行了轨迹规划仿真，仿真结果表明：改进的三次B样条曲线轨迹规划方法，在相同运动学约束条件下能够得到更好的规划结果，所改进的算法具有一定的实际工程应用价值。